الدرس الرابع: حل استراتيجية حل المسألة
١- اذكر مزية واحدة لاستعمال استراتيجية ((تمثيل المسألة)) لحل المسائل.
المزية هي يمكن التنبؤ بما حدث فعلياً.
٢- اكتب: مسألة يمكن حلها باستراتيجية ((تمثيل المسألة)) ثم استعمل الاستراتيجية لحلها وفسر إجابتك.
بكم طريقة يمكن ترتيب أربعة أشخاص في السيارة، اثنين في المقدمة واثنين في الخلف وثلاثة منهم يمكنهم القيادة؟
١٨ طريقة ممكنة
استعمل استراتيجية "تمثيل المسألة" لحل المسائل ٣ - ٥:
٣- نقود: اشترى أحمد عصير تفاح وقطع شوكولاتة بـ ٤٥,٥ ريالاً، ودفع للبائع ٥٠ ريالاً، فبكم طريقة يمكن أن يسترد الباقي إذا كان لدى البائع قطع من الفئتين: ريال، ريال؟
أفهم:
- اشترى أحمد بمبلغ ٤٥,٤
- دفع ٥٠ ريال
- المطلوب إيجاد بكم طريقة يمكن له أن يسترد الباقي مع العلم أن البائع لديه قطع من فئتين ريال ٠,٥ نصف
خطط: بتمثيل المسألة
حل: الباقي = ٥٠ - ٤٥,٥ = ٤,٥ ريال
- الطريقة الأولى: ٤ ريال ونصف ريال
- الطريقة الثانية: ٨ ورقات من فئة نصف ريال
- الطريقة الثالثة: ٣ ريال و٣ نصف ريال
- الطريقة الرابعة: ورقة من فئة ريال و٤ ورقات من فئة نصف ريال
- الطريقة الخامسة: ورقتين من فئة ريال و٥ ورقات من فئة نصف ريال
تحقق: حساب ناتج كل طريقة.
٤- رياضة: طول ملعب ٨٤ قدماً فإذا ركض مبارك ٢٠ قدماً إلى الأمام و٨ أقدام إلى الخلف فكم مرة أخرى عليه أن يكرر العملية حتى يصل إلى نهاية الملعب؟
أفهم:
- طول ملعب = ٨٤ قدم
- ركض مبارك ٢٠ للأمام
- ركض ٨ إلى الخلف
خطط: بتمثيل المسألة.
حل: المسافة بعد الركض = ٢٠ - ٨ = ١٢ قدم.
إذن يحتاج إلى ٨٤ ÷ ١٢ = ٧ عمليات للوصول إلى النهاية.
تحقق: قم بالحل عملياً.
٥- مكتبة: أراد ماهر أن يرتب خمسة كتب لديه على الرف، بحيث يكون كتاب التفسير أولها وكتاب الاجتماعيات آخرها، فبكم طريقة يمكن ترتيب الكتب الخمسة على الرف؟
أفهم:
- يوجد ٥ كتب يريد ماهر ترتيبهم.
- بحيث يكون أول كتاب هو التفسير وآخر كتاب هو الاجتماعيات.
خطط: بتمثيل المسألة.
حل:
- بما أن الكتاب الأول والأخير ثابتان.
- إذن يمكن ترتيب الثلاث كتب الباقية بـ ٣ × ٢ = ٦ طرق
تحقق: التحقق من المسألة عملياً.
استعمل الاستراتيجية المناسبة لحل المسائل ٦ - ١٢:
٦- قياس: صمم فهد حديقة منزله على شكل مستطيل، على أن يكون محيطها يساوي مرة من محيط المستطيل الظاهر في الصورة أوجد محيط الحديقة.
أفهم:
- طول المستطيل = ٨ م وعرضه ١٦ م
- طول الحديقة = ٢,٢٥ مرة من محيط المستطيل.
- المطلوب إيجاد محيط الحديقة.
خطط: التبرير المنطقي.
حل:
- محيط المستطيل = (٨ + ١٦) × ٢ = ٤٨ م
- محيط الحديقة = ٤٨ × ٢,٢٥ = ١٠٨ م
تحقق: ١٠٨ ÷ ٢,٢٥ = ٤٨ م وهو محيط المستطيل، إذن الإجابة صحيحة.
٧- جبر: أكمل النمط الآتي: ١٠٠، ٩٨، ٩٤، ، ٨٠،
أفهم: أكمل النمط الآتي: ١٠٠، ٩٨، ٩٤، ، ٨٠،
خطط: البحث عن نمط.
حل:
بالنظر إلى النمط نستنتج أنه في كل مرة ينقص ضعف العدد في المرة السابقة.
وعلى ذلك يكون النمط ١٠٠، ٩٨، ٩٤، ٨٨، ٨٠، ٧٠
تحقق: بإعادة الحل عدة مرات.
٨- نقود: في اليوم للعيد كان مع نورة مبلغ من المال أقرضت أختها منه ٥٠ ريالاً ثم صرفت نصف الباقي وفي اليوم الثاني للعيد أعطاها عمها ١٠٠ريال وبعد أن صرفت ٩٠ ريالاً بقي معها ١١٠ ريالات فما المبلغ الذي كان مع نورة في اليوم الأول للعيد؟
أفهم: في اليوم الأول مع نورة مبلغ وأقرضت أختها ٥٠ ريال ثم صرفت نصف الباقي.
في اليوم الثاني أعطاها عمها ١٠٠ وصرفت ٩٠ ريال وبقي معها ١١٠ ريال.
المطلوب معرفة كم معها اليوم الأول.
خطط: الحل عكسياً.
حل:
كام معها ١٠٠ ريال في اليوم الثاني وصرفت ٩٠ وبقي معها ١١٠.
١٠ ريال منهم باقي ما معها ثاني يوم و١٠٠ ريال باقي مما كان معها أول يوم.
وبما أنها تبقي معها ١٠٠ ريال كنصف للباقي، إذن كان معها ٢٠٠ ريال.
وبما أنها أقرضت أختها ٥٠ ريال، إذن كانت تملك ٢٥٠ ريال.
تحقق: ٢٥٠ ÷ ٥٠ = ٢٠٠
٢٠٠ ÷ ٢ = ١٠٠، وهو ما تبقى معها أول يوم، إذن الإجابة صحيحة.
٩- زي: ما عدد الخيارات التي يمكن لقاسم أن يختار بها زيه من بين: غترة بيضاء أو حمراء أو سكرية مع ثوب أبيض أو بني أو أسود؟
أفهم:
- يملك قاسم غترة بيضاء وحمراء وسكرية.
- ويملك ثوب أبيض وبني وأسود.
- المطلوب معرفة عدد الخيارات التي يمكن لقاسم أن يختار بها زيه.
خطط: بتمثيل المسألة.
حل:
عدد الخيارات = عدد الغتر × عدد الثياب.
عدد الخيارات = ٣ × ٣ = ٩ خيارات.
تحقق: الحل بطريقة الرسم الشجري.
١٠- اصطفاف: تقف علياء وفاطمة ومها وعبير في حظ مستقيم فبكم طريقة يمكن ترتيب هؤلاء البنات؟
أفهم:
- تقف علياء وفاطمة ومها وعبير في خط مستقيم.
- المطلوب إيجاد عدد الطرق التي يمكن أن ترتب بها هؤلاء البنات.
خطط: بتمثيل المسألة.
حل:
(علياء، فاطمة، مها، عبير)، (علياء، مها، عبير، فاطمة)، (علياء، عبير، فاطمة، مها)،
(فاطمة، مها، عبير، علياء)، (فاطمة، عبير، علياء، مها)، (فاطمة، علياء، مها، عبير)،
(مها، عبير، علياء، فاطمة)، (مها، علياء، فاطمة، عبير)، (مها، فاطمة، عبير، علياء)،
(عبير، علياء، فاطمة، مها)، (عبير، فاطمة، مها، علياء)، (عبير، مها، علياء، فاطمة).
إذن يمكن ترتيبهم بـ ١٢ طريقة.
تحقق: بإعادة الحل عدة مرات.
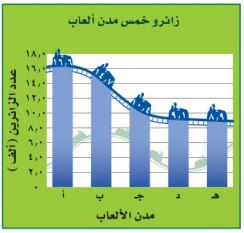
١١- ألعاب: بالاعتماد على الرسم أدناه كيف تقارن بين زائري المدينة (أ) والمدينة (هـ)؟
أفهم:
عدد سكان أ = ١٦,٦
عدد سكان هـ = ٨,٩
خطط: التبرير المنطقي.
حل:
بمقارنة عدد سكان المدينتين ينتج أن عدد زائري المنتزه أ مثلاً عدد زائري المنتزه هـ تقريباً.
تحقق: بإعادة الحل عدة مرات.
١٢- الحس العددي: إذا كان احتمال سحب كرة زرقاء من صندوق هو ، واحتمال سحب كرة حمراء هو ، وكان عدد الكرات الخضراء مثلي عدد الكرات الصفراء في الصندوق فأعط إمكانية واحدة لأعداد الكرات في الصندوق.
أفهم:
احتمال سحب كرة زرقاء هو
احتمال سحب كرة حمراء هو
عدد الكرات الخضراء مثلي عدد الكرات الصفراء في الصندوق
المطلوب إيجاد إمكانية واحداً لأعداد الكرات في الصندوق
خطط: بتمثيل المسألة.
حل:
بما أن المقام = ١٠ إذن عدد الكرات = ١٠
احتمال كرة زرقاء = ٤، احتمال كرة حمراء = ٣
إذن بقي ٣ كرات.
وبما أن عدد الكرات الخضراء = مثلي عدد الكرات الصفراء.
فيكون عدد الكرات الخضراء = ٢، عدد الكرات الصفراء = ١
تحقق: ١ أصفر + ٢ أخضر + ٣ أحمر + ٤ أزرق = ١٠، إذن الإجابة صحيحة.
مشاركة الدرس
الاختبارات
اختبار الكتروني: استراتيجية حل المسألة
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">

.JPG)
.JPG)
.JPG)

.JPG)




النقاشات