اختبار الفصل
حدد ما إذا كانت العبارات الآتية تصف ارتباطاً أو سببية، ثم فسر إجابتك:
1) عندما يرى محمود البرق، فإنه يسمع الرعد بعد ذلك.
ارتباط: على الرغم من أن البرق يسبق الرعد دائماً، ولكن هذا لا يعني أن البرق هو الذي يسبب الرعد.
2) عندما يركض نايف عند مدخل المدرسة، فإنه يكون متأخراً عن المدرسة.
ارتباط: مع وجود علاقة بين الحدثين، إلا أن نايفاً قد يركض لسبب آخر.
حدد ما إذا كانت كل دراسة مسحية فيما يأتي تتبنى عينة متحيزة أو غير متحيزة، ثم فسر إجابتك:
3) استطلع صاحب مخزن يبيع من خلال الشبكة العنكبوتية زبائنه عن أهمية وجود الإنترنت في المنزل.
متحيزة؛ لأن الناس الذين تم استطلاع آرائهم يرون أهمية كبرى لوجود الإنترنت، فهم يشترون من خلاله.
4) يختار معلم 5 أسماء لطلاب يدرسهم؛ لإلقاء كلمة الصباح بعد أن يقوم بوضع الأسماء جميعها في سلة ويخلطها.
غير متحيزة؛ كل فرد في المجتمع له الفرصة نفسها ليكون في العينة.
أي مقاييس النزعة المركزية يصف كلاً من البيانات الآتية بصورة أفضل؟ ولماذا؟
5)
| درجات اختبار | ||||
| 4 | 4 | 3 | 3 | 3 |
| 4 | 5 | 5 | 4 | 4 |
| 3 | 3 | 3 | 3 | 4 |
| 3 | 3 | 3 | 4 | 4 |
| 4 | 5 | 3 | 4 | 3 |
المتوسط؛ لأن البيانات لا تتضمن قيماً متطرفة.
6)
| الطول بالبوصة | ||||
| 61 | 64 | 62 | 61 | 64 |
| 63 | 65 | 61 | 66 | 83 |
| 84 | 63 | 62 | 65 | 61 |
| 61 | 62 | 66 | 63 | 61 |
الوسيط؛ لأن البيانات تتضمن قيماً متطرفة، ولا توجد فجوات كثيرة في المنتصف.
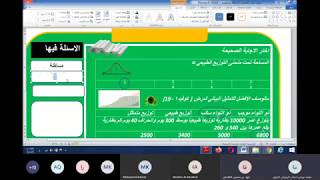
فيما يأتي المتوسط والانحراف المعياري لمجموعة من البيانات تتوزَّع توزيعاً طبيعياً، أوجد الاحتمال المطلوب في كل منها:
7)
97.5%
8)
84%
يحتوي كيس على 10 كرات زجاجية زرقاء، و8 كرات حمراء، و12 خضراء، وجميعها متماثلة، سحبت كرتان واحدة تلو الأخرى، أوجد
الاحتمال لكل من:
9) الكرة الثانية حمراء، علماً بأن الكرة الأولى زرقاء دون إرجاع.
10) الكرة الثانية زرقاء، علماً بأن الكرة الأولى خضراء مع الإرجاع.
11) اختبارات: أعطى المعلم أيمن طلابه الفرصة لإعادة أحد الاختبارات، كما عقد درس مراجعة اختياري يوم الخميس قبل إعادة
الاختبار لمن يرغب، بعض الطلاب تحسَّن أداؤهم، والبعض الآخر لم يتحسن، والجدول أدناه يبين ذلك، إذا اختير طالب عشوائياً، فأوجد:
| تحسن | لم يتحسن | |
| حضر المراجعة | 12 | 3 |
| لم يحضر المراجعة | 4 | 6 |
a) احتمال أن يكون قد تحسن علماً بأنه حضر المراجعة.
أو 80%
b) احتمال أنه لم يحضر المراجعة علماً بأنه لم يتحسن.
أو 67%
12) اختيار من متعدد: شارك 10 طلاب من الصف الأول الثانوي، و12 طالباً من الصف الثاني الثانوي في السحب على 5 جوائز، إذا كان السحب عشوائياً، فما احتمال أن يكون الرابحون 3 من الصف الأول الثانوي، وطالبين من الصف الثاني الثانوي؟
- 0.46% تقريباً.
- 0.25% تقريباً.
- 70% تقريباً.
- 30% تقريباً.
13) سحبت كرتان معاً من صندوق يحتوي على 3 كرات زرقاء، وكرتين حمراوين، إذا كان المتغير العشوائي X يدل على عدد الكرات الزرقاء المسحوبة، فكون جدول التوزيع الاحتمالي للمتغير العشوائي X.
14) طقس: أخبر الراصد الجوي أن احتمال سقوط المطر في كل يوم من الأيام السبعة القادمة %40، أوجد احتمال أن يسقط المطر في يومين من هذه الأيام على الأقل.
84.1% تقريباً.
15) حديقة: يخطط يعقوب لزرع 24 شجرة أزهار، إذا علمت أن البذور التي أحضرها لأزهار من اللونين الأبيض والأزرق، وأنها لم
تزهر بعد، ولكنه يعلم أن احتمال الحصول على زهرة زرقاء % 75، فما احتمال حصوله على 20 زهرة زرقاء على الأقل؟
0.24665 تقريباً أو 24.7%
مشاركة الدرس
الاختبارات
اختبار الكتروني: درس اختبار الفصل
4720%
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]%;" role="progressbar" aria-valuenow="
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">

.JPG)
.JPG)

النقاشات