اكتب معادلة وحلها لإيجاد قيمة س، بحيث يكون محيطا المضلعين متساويين.

٢ن + ٤ ن + ٣ن + ٢ = ن + ٢ + ٢ن + ٤ ن + ١ + ن + ٢

$\bcancel{\mathrm{٢}ن }+ \bcancel{\mathrm{٤} ن} + \mathrm{٣}ن + \bcancel{\mathrm{٢}} = ن +\bcancel{ \mathrm{٢}} + \bcancel{\mathrm{٢}ن} + \bcancel{\mathrm{٤} ن }+ \mathrm{١} + ن + \mathrm{٢}$

٣ن = ٢ن + ٣

ن = ٣

إيجاد س الشكل الأول

٢× ٣ + ٤ × ٣ + ٣ × ٣ + ٢ = س

٦ + ١٢ + ١١ = س

س = ٢٩

إيجاد س الشكل الثاني

٣ + ٢ + ٢ × ٣ + ٤ × ٣ + ١ + ٣ + ٢ = س

٥ + ٦ + ١٢ + ١ + ٥ = س

١١ + ١٢ + ٦ = س

س = ٢٩

حل أسئلة اختبار منتصف الفصل السابع

استعمل خاصية التوزيع في إعادة كتابة كل عبارة مما يأتي:

١- ٣(س+٢)

٣س + ٦

٢- -٢(أ-٣)

-٢أ + ٦

٣- ٥(٣جـ -٧)

١٥ج - ٣٥

٤- -٤ (٢ن +٣)

-٨ن -١٢

بسط كل عبارة مما يأتي:

٥- ٢أ -١٣أ

أ (٢-١٣) = ١١أ

٦- ٦ب + ٥ -٦ب

$\bcancel{\mathrm{٦}ب} + \mathrm{٥} \bcancel{-\mathrm{٦}ب}$ = ٥

٧- ٢م +٥ -٨م

٥ + ٢م -٨ م

= ٥ - ٦ م

٨- ٧س +٢ -٨س +٥

= -س +٧٧س +٢ -٨س + ٥

= ٧- س

٩- عين الحدود، والحدود المتشابهة، والمعاملات والثوابت في العبارة: ٥ -٤س +س -٣.

الحدود: ٥، -٤س، س، -٣

الحدود المتشابهة: -٤س، س

المعاملات: -٤، ١

الثوابت: -٣، ٥

حل كل معادلة فيما يأتي ثم تحقق من صحة الحل:

١٠- ٣ م + ٥ = ١٤

٣م = ١٤ - ٥

٣م = ٩

م = ٣

للتحقق: ٣ م + ٥ = ١٤

٣(٣) + ٥ = ١٤

٩ + ٥ = ١٥

١٤ = ١٤ c

١١- -٢ ك + ٧ = - ٣

-٢ك = -٣ -٧

-٢ك = -١٠

ك = ٥

للتحقق: -٢ ك + ٧ = - ٣

-٢(٥) + ٧ = -٣

-١٠ +٧ = -٣

-٣ = -٣ c

١٢- ١١ = $\frac{\mathrm{١}}{\mathrm{٣}}$أ + ٢

$\frac{\mathrm{١}}{\mathrm{٣}}$أ = ١١ - ٢

$\frac{\mathrm{١}}{\mathrm{٣}}$أ = ٩

‌أ = ١٨

١٣- -١٥ = -٧ -ي

ي = ١٥ - ٧

ي = ٨

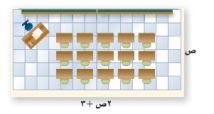
١٤- اختيار من متعدد: يبين الشكل أدناه مخطط غرفة صفية.

إذا كان محيط الغرفة ٧٨ قدماً، فكم عرضها؟

أ. ١٢ قدماً.

ب. ١٥ قدماً.

ج. ٢٥ قدماً.

د. ٢٧ قدماً.

محيط المستطيل = (الطول + العرض) × ٢

٧٨ = (٢ص + ٣ + ص) × ٢

٧٨ = ٤ ص + ٦ + ٢ص

٦ ص = ٧٨ - ٦

٦ ص = ٧٢

ص = ١٢

١ ٥- تدريب: استعداداً لسباق الدراجات يقطع سعد بدراجته المسافة يومي الثلاثاء والخميس ويقطع مسافة ٢٠ كيلو متراً يوم السبت وعليه يكون مجموع المسافة التي يقطعها في الأيام الثلاثة ٥٠ كيلو متراً حل المعادلة ٢م + ٢٠ = ٥٠ لإيجاد المسافة التي يقطعها سعد في كل من يومي الثلاثاء والخميس.

٢م +٠ ٢ = ٥٠

٢م = ٣٠

م = ١٥

حول كل جملة فيما يأتي إلى معادلة ثم حلها:

١٦- يزيد العدد ٩ على ناتج قسمه عدد على ٣ بمقدار ١٤

٩ - $\frac{س}{\mathrm{٣}}$ = ١٤

- $\frac{س}{\mathrm{٣}}$ = ١٤ - ٩

س = -١٥

١٧- ناتج قسمة عدد ما على (-٧) مطروحاً منه ٤ يساوي (-١١)

$\frac{-س}{\mathrm{٧}} -\mathrm{٤} =$- ١١

- س - ٢٨ = -٧٧

- س = -٧٧ + ٢٨

- س = -٤٩

س = ٤٩

١٨- الفرق بين ١٠و ثلاثة أمثال عدد ما يساوي ١٧

٣س - ١٠ = ١٧

٣س = ٢٧

س = ٩

١٩- اتصالات: تتقاضى شركة اتصالات ٤٥ ريالاً رسوماً شهرية كما تتقاضى ٠,١٥ ريال عن كل دقيقة أو جزء منها يتحدثها المتصل، اكتب معادلة وحلها لإيجاد عدد الدقائق التي تحدثها متصل كانت فاتورته الشهرية ١١٢,٥ ريالاً.

٤٥ + ٠,١٥س = ١١٢,٥

٠,١٥س = ١١٢,٥ - ٤٥

٠,١٥س = ٦٧,٥

س = $\frac{\mathrm{٥},\mathrm{٦٧}}{\mathrm{١٥},\mathrm{٠}}$ = $\frac{\mathrm{٦٧٥٠}}{\mathrm{١٥}}$ = ٤٥٠

حل كل معادلة فيما يأتي ثم تحقق من صحة الحل:

٢٠- ٣س + ٧ = ٢س

س = -٧

٢١- ٧ب -٦ = ٤ب

٧ب -٤ب = ٦

٣ب = ٦

ب = ٢

٢٢- ٣ ص -٥ = ٥ص + ٧

٥ص - ٣ص = -٥ -٧

٢ص = -١٢

ص = -٦

٢٣- ٤م +٧ = -٣ م + ٤٩

٧م = ٤٩ - ٧

٧م = ٤٢

م = ٦

٢٤- قياس: اكتب معادلة وحلها لإيجاد قيمة س، بحيث يكون محيطا المضلعين متساويين.

٢ن + ٤ ن + ٣ن + ٢ = ن + ٢ + ٢ن + ٤ ن + ١ + ن + ٢

$\bcancel{\mathrm{٢}ن }+ \bcancel{\mathrm{٤} ن} + \mathrm{٣}ن + \bcancel{\mathrm{٢}} = ن +\bcancel{ \mathrm{٢}} + \bcancel{\mathrm{٢}ن} + \bcancel{\mathrm{٤} ن }+ \mathrm{١} + ن + \mathrm{٢}$

٣ن = ٢ن + ٣

ن = ٣

إيجاد س الشكل الأول

٢× ٣ + ٤ × ٣ + ٣ × ٣ + ٢ = س

٦ + ١٢ + ١١ = س

س = ٢٩

إيجاد س الشكل الثاني

٣ + ٢ + ٢ × ٣ + ٤ × ٣ + ١ + ٣ + ٢ = س

٥ + ٦ + ١٢ + ١ + ٥ = س

١١ + ١٢ + ٦ = س

س = ٢٩