اكتب متتابعة حسابية يكون أساسها $\frac{-\mathrm{١}}{\mathrm{٣}}$ ,

بوضع ن = ١ والتعويض في الحد النوني $\frac{-\mathrm{١}}{\mathrm{٣}}$ ن تكون حدود المتتابعة هي $\frac{-\mathrm{١}}{\mathrm{٣}}$ ، - $\frac{\mathrm{٢}}{\mathrm{٣}}$ ، -١

حل أسئلة تدرب وحل المسائل

بين ما إذا كانت كل متتابعة حسابية أم لا، وإذا كانت كذلك، فأوجد أساسها، والحدود الثلاثة التالية فيها:

١٣- ٢٠، ٢٤، ٢٨، ٣٢، ٣٦،.....

الفرق ثابت بين كل حدين وهو ٤ وعليه تكون المتتابعة حسابية وأساسها ٤, وتكون الحدود الثلاثة التالية هي ٤٠، ٤٤، ٤٨

١٤- ١، ١٠، ١٠٠، ١٠٠٠، ١٠٠٠٠،.....

الفرق غير ثابت وعليه تكون المتتابعة غير حسابية.

١٥- ١٨٩، ٦٣، ٢١، ٧، $\frac{\mathrm{١}}{\mathrm{٣}}\mathrm{٢}$،.....

الفرق غير ثابت وعليه تكون المتتابعة غير حسابية.

١٦- -٦، -٤، -٢، ٢،.....

الفرق ثابت بيت الحدود وهو ٢ وعليه تكون المتتابعة حسابية أساسها ٢ وتكون الحدود الثلاثة التالية هي ٤، ٦، ٨

١٧- ١، ٢، ٥، ١٠، ١٧،.....

الفرق غير ثابت وعليه تكون المتتابعة غير حسابية.

١٨- ٤، $\frac{\mathrm{١}}{\mathrm{٢}}\mathrm{٦}$،٩، $\frac{\mathrm{١}}{\mathrm{٢}} \mathrm{١١}$، ١٤،.....

الفرق ثابت بين الحدود وهو ٢,٥ وعليه تكون المتتابعة حسابية وأساسها ٢,٥ وتكون الحدود الثلاثة التالية هي ١٦,٥، ١٩، ٢١,٥

بين ما إذا كانت كل متتابعة فيما يأتي حسابية أم لا، وإذا كانت كذلك فأوجد أساسها.

١٩- ٦ ن -٣

بكتابة بعض حدود المتتابعة من خلال التعويض:

• عندمان = ١، الحد الأول = ٦ - ٣ = ٣
• عندمان = ٢، الحد الأول = ١٢ -٣ = ٩
• عندمان = ٣، الحد الأول = ١٨ - ٣ = ١٥

لاحظ أن الفرق بين كل حدين متتاليين ثابت وهو ٦ فالمتتابعة حسابية أساسها ٦

٢٠- ن^٣

بكتابة بعض حدود المتتابعة من خلال التعويض:

• عندما ن = ١، الحد الأول = ١
• عندما ن = ٢، الحد الأول = ٨
• عندما ن = ٣، الحد الأول = ٢٧

لاحظ أن الفرق بين كل حدين متتاليين غير ثابت فالمتتابعة ليست حسابية.

٢١- $\frac{\mathrm{١}}{ن}$

بكتابة بعض حدود المتتابعة من خلال التعويض:

• عندما ن = ١، الحد الأول = ١
• عندما ن = ٢، الحد الأول = ٨٠,٥
• عندما ن = ٣، الحد الأول = $\frac{\mathrm{١}}{\mathrm{٣}}$

لاحظ أن الفرق بين كل حدين متتاليين غير ثابت فالمتتابعة ليست حسابية.

٢٢- ٩ - ٣ن

بكتابة بعض حدود المتتابعة من خلال التعويض:

• عندما ن = ١، الحد الأول = ٩ - ٣ = ٦
• عندما ن = ٢، الحد الأول = ٩ - ٦ = ٣
• عندما ن = ٣، الحد الأول = ٩ - ٩ = ٠

لاحظ أن الفرق بين كل حدين متتاليين ثابت وهو ٣ فالمتتابعة حسابية أساسها ٣

اكتب عبارة يمكن استعمالها لإيجاد الحد النوني لكل متتابعة فيما يأتي، ثم اكتب الحدود الثلاثة التالية فيها:

٢٣- ٢، ٤، ٦، ٨،.....

الفرق الثابت بين الحدود يساوي ٢ وعليه تكون العبارة التي يمكن استعمالها هي ٢ن وتكون الحدود التالية هي ١٠، ١٢، ١٤.

٢٤- ١٢، ٢٤، ٣٦، ٤٨،......

الفرق الثابت بين الحدود يساوي ١٢ وعليه تكون العبارة التي يمكن استعمالها هي ١٢ن وتكون الحدود التالية هي ٦٠، ٧٢، ٨٤.

٢٥- $\frac{\mathrm{١}}{\mathrm{٣}}،\frac{\mathrm{٢}}{\mathrm{٣}}$، ١،$\frac{\mathrm{١}}{\mathrm{٣}}\mathrm{١}$،.....

وبالمثل تكون العبارة التي يمكن استعمالها هي $\frac{\mathrm{١}}{\mathrm{٣}}$ ن وتكون الحدود الثلاثة التالية هي $\frac{\mathrm{٢}}{\mathrm{٣}}\mathrm{١}، \mathrm{٢}، \frac{\mathrm{١}}{\mathrm{٣}}\mathrm{٢}$

٢٦- $\frac{\mathrm{٢}}{\mathrm{٥}}،\frac{\mathrm{٤}}{\mathrm{٥}}،\frac{\mathrm{١}}{\mathrm{٥}}\mathrm{١}،\frac{\mathrm{٣}}{\mathrm{٥}}\mathrm{١}،$......

العبارة التي يمكن استعمالها هي $\frac{\mathrm{٢}}{\mathrm{٥}}$ ن وتكون الحدود الثلاثة المتتالية هي ٢، $\frac{\mathrm{٢}}{\mathrm{٥}}\mathrm{٢}،\frac{\mathrm{٤}}{\mathrm{٥}}\mathrm{٢}$

٢ ٧- ٥، ٩، ١٣، ١٧،.....

العبارة التي يمكن استعمالها هي؛ ٤ن + ١ وتكون الحدود الثلاثة التالية هي ٢١، ٢٥، ٢٩.

٢٨- ١، ٤، ٧، ١٠،......

العبارة التي يمكن استعمالها هي؛ ٣ن - ٢ وتكون الحدود الثلاثة التالية هي ١٣، ١٦، ١٩.

اكتب عبارة لإيجاد الحد النوني في كل متتابعة حسابية فيما يأتي، واستعملها لإيجاد قيمة الحد عند ن المعطاة:

٢٩- ٣، ٧، ١١، ١٥،.....؛ ن = ٨

الحد النوني = ٤ن -١

عند ن = ٨ يكون الحد النوني = ٣١

٣٠- ٢٣، ٢٥، ٢٧، ٢٩،.....؛ ن = ١٢

الحد النوني = ٢ن +٢١

عند ن = ١٢ يكون الحد النوني = ٤٥

٣١- ١٠، ٥، ٠، -٥،......؛ ن = ٢١

الحد النوني = ١٥ - ٥ن

عند ن = ٢١ يكون الحد النوني = -٩٠

٣٢- ٢٧، ١٩، ١١، ٣،.......؛ ن = ١٧

الحد النوني = ٣٥ - ٨ ن

عند ن = ١٧ يكون الحد النوني = -١٠١

رياضة: للسؤالين ٣٣ - ٣٤ استعمل الجدول المجاور.

٣٣- إذا أكمل عادل النمط المبين في الجدول فكم دقيقة سيمشي يومياً خلال الأسبوع الخامس؟

أساس المتتابعة الآتية هو ٨ والحد النوني = ٨ن فيكون الزمن في الأسبوع الخامس = ٥ × ٨ = ٤٠ دقيقة.

٣٤- هل يتناسب وقت مشي عادل مع عدد الأسابيع التي مشى فيها؟ فسر إجابتك.

نعم لأن نسبة المشي إلى الأسبوع ١: ٨ لكل أسبوع.

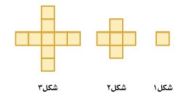
هندسة: للسؤالين ٣٥- ٣٦ استعمل الشكل المجاور.

٣٥- كم مربعاً سيكون في الشكل رقم ١٨؟

الأساس هو ٤ يكون الحد النوني = ٤ن -٣ وعليه يكون الشكل رقم ١٨ فيه ٦٩ مربعاً.

٣٦- هل يتناسب عدد المربعات في كل شكل مع رقم الشكل؟ فسر إجابتك.

لا، نسبة عدد المربعات إلى رقم الشكل غير ثابت.

٣٧- مسألة مفتوحة: اكتب متتابعة حسابية يكون أساسها $\frac{-\mathrm{١}}{\mathrm{٣}}$,

بوضع ن = ١ والتعويض في الحد النوني $\frac{-\mathrm{١}}{\mathrm{٣}}$ ن تكون حدود المتتابعة هي $\frac{-\mathrm{١}}{\mathrm{٣}}$، - $\frac{\mathrm{٢}}{\mathrm{٣}}$، -١

٣٨- تبرير: بين فيما إذا كانت العبارة الآتية صحيحة دائماً أو أحياناً أو غير صحيحة أبداً، فسر إجابتك.

((المتتابعة التي يضاف فيها عدد إلى أي حد للحصول على الحد الذي يليه هي متتابعة حسابية))

أحياناً: تكون المتتابعة حسابية عند إضافة القيمة نفسها لكل حد للحصول على الحد التالي له.

٣٩- تحد: اكتب عبارة يمكن استعمالها لإيجاد الحد النوني للمتتابعة الموضحة في الجدول المجاور.

العابرة هي ٣ن + ٥

٤٠- اكتب: مسألة من الواقع تمثل متتابعة حسابية، ثم حلها.

المسألة ٣٣ السابقة.

٤١- ما العبارة التي تمثل الحد النوني في المتتابعة المبينة في الجدول الآتي؟

أ. ن -٠,٤

ب. $\frac{ن}{\mathrm{٥}}$

جـ. $\frac{\mathbf{٣}}{\mathbf{٥}}$ ن

د. ن + ٠,٦

٤٢- اختيار من متعدد: تصف العبارة -١٢ -٤(ن-١) نمطاً عددياً، فإذا كانت ن تمثل الحد ن في المتتابعة، فأي نماط الأعداد التالية تصفها العبارة؟

أ. -١٢، -١٦، -٢٠، -٢٤،.....

ب. -١٢، -٨، -٤، ٠،.....

جـ. ١٢، ٨، ٤، ٠،.....

د. ١٢، ١٦، ٢٠، ٢٤،.....