تدرب وحل المسائل
استعمل PQRS المبين جانباً لإيجاد كل مما يأتي:
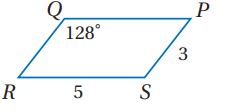 7)
7)
الحل:
كل زاويتين متحالفتين مجموعهم = 180º.
8) QR
الحل:
كل ضلعين متناظرين متطابقين في متوازي الأضلاع.
QR = PS = 3cm
9) QP
الحل:
كل ضلعين متناظرين متطابقين في متوازي الأضلاع.
QP = RS = 5 cm
10) .
الحل:
كل زتويتين متقابلتين متساويتين.
11) ستائر: في الشكل المقابل صورة لشرائح ستائر النوافذ المتوازية دائماً لنسمح بدخول أشعة الشمس في FGHJ إذا كان فأوجد كلاً مما يأتي:
.JPG) a)
a)
الحل:
كل ضلعين في متوازي الأضلاع متقابلين متطابقين.
FG = JH =1in.
b)
الحل:
كل ضلعين في متوازي الأضلاع متقابلين متطابقين.
FG = GH= in
c) .
الحل:
كل زاويتين في متوازي الأضلاع متقابلتين متطابقتين.
d)
الحل:
كل زاويتين متحالفتين مجموعهم = 180º.
جبر: أوجد قيمتي X,Y في كل من متوازيات الأضلاع الآتية:
12)
الحل:
بما أن الشكل متوازي أضلاع إذن كل ضلعين متقابلين متطابقين.
13)
الحل:
كل زاويتين متحالفتين مجموعهم = 180º.
14)
الحل:
قطرا متوازي الأضلاع ينصف كل منهما الآخر.
هندسة إحداثية: أوجد إحداثيات نقطة تقاطع قطري WXYZ المعطاة رؤوسه في كل من السؤالين الآتيين:
15)
الحل: بما أن قطري متوازي الأضلاع ينصف كلاً منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من أوجد منتصف التي طرفيها
(صيغة نقطة المنتصف).
(2.5,2.5) (بالتبسيط).
إذاً إحداثيات نقطة تقاطع قطريهما (2.5,2.5)
16)
الحل: بما أن قطري متوازي الأضلاع ينصف كلاً منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من أوجد نقطة منتصف التي طرفاها
(صيغة نقطة المنتصف).
(بالتبسيط).
إذن إحداثيات نقطة تقاطع قطري هما .
برهان: اكتب برهاناً ذا عمودين فيما يأتي:
17) المعطيات:
المطلوب:
الحل:
المعطيات: متوازي الأضلاع WXTV , ZYVT
المطلوب:
البرهان:
العبارات(المبررات):
1) WXTV ,ZYVT متوازي أضلاع (معطى).
2) (الأضلاع المتقابلة في متوازي الأضلاع متطابقة).
3) (خاصية التعدي).
جبر: استعمل ABCD المبين جانباً لإيجاد كل مما يأتي:
18) x
الحل: كل ضلعين متقابلين متطابقين.
19) y
الحل:
20)
الحل:
21)
الحل:
22)
الحل:
23)
الحل:
24) هندسة إحداثية: إذا كانت رؤوساً في فأوجد إحداثيات الرأس D وضح تبريرك.
الحل:
ولتعيين الرأس D ابدأ من الرأس A وتحرك إلى الأسفل 6 وحدات وإلى اليمين وحدتين.
إذن الرأس D = (0 ,-1).
برهان: اكتب برهاناً من النوع المحدد في كل مما يأتي:
25) برهاناً ذا عمودين
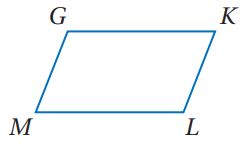
المعطيات: GKLM متوازي أضلاع.
المطلوب: إثبات أن كل زاويتين في الأزواج التالية متكاملتان
(النظرية 1.5)
الحل:
البرهان:
العبارات (المبررات):
1) متوازي الأضلاع GKLM (معطى).
2) (الأضلاع المتقابلة لمتوازي الأضلاع متوازية).
3)
زوايا متكاملة: (كل زاويتين متقابلتين في متوازي الأضلاع متكاملتين).
26) برهاناً ذا عمودين.
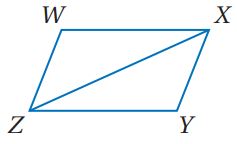
العطيات: WXYZ متوازي أضلاع.
المطلوب:
(النظرية 1.8)
الحل:
البرهان:
العبارات (المبررات):
1) متوازي الأضلاع WXYZ (معطى).
WX=ZY ,XY = WZ ضلعين متقابلين متطابقين.
XZ = ZX خاصية الانعكاس.
3) (SSS)
27) برهاناً ذا عمودين.
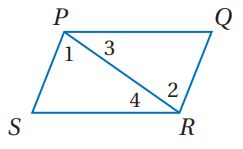
المعطيات: PQRS متوازي أضلاع.
المطلوب:
(النظرية 1.3)
الحل:
البرهان:
العبارات (المبررات):
1) متوازي الأضلاع PQRS (معطى).
2) ارسم قطعة مستقيمة مساعدة PR (قطر PQRS) وسم الزوايا 1, 2, 3, 4 كما هو مبين.
3) (الأضلاع المتقابلة لمتوازي الأضلاع متوازية).
4) (نظرية الزوايا المتبادلة داخلياً).
5) PR =RP (خاصية الانعكاس).
6)
7) (العناصر المتناظرة في مثلثين متطابقين متطابقة).
28) برهاناً حراً.
المعطيات: ACDE متوازي أضلاع.
المطلوب: القطران ينصف كل منهما الآخر (النظرية 1.7).
الحل:
البرهان: معطى أن ACDE متوازي أضلاع.
بما أن الأضلاع المتقابلة لتوازي الأضلاع متطابقة فإن
ومن تعريف متوازي الأضلاع
وتكون لأن الزوايا المتبادلة داخلياً متطابقة.
لأن الزوايا المتبادلة داخلياً متطابقة إذن حسب ASA و لأن العناصر المتناظرة في المثلثين المتطابقين متطابقة ومن تعريف منصف القطعة المستقيمة فإن تنصف و تنصف
29) هندسة إحداثية: استعن بالشكل المجاور في كل مما يأتي:
a) استعمل صيغة المسافة بين نقطتين لتحديد ما إذا كان قطرا JKLM ينصف كل منهما الآخر وضح اجابتك.
الحل:
بما أن JP = LP , MP = KP فإن القطرين ينصف كل منهما الآخر.
b) حدد ما إذا كان قطرا JKLM متطابقين وضح اجابتك.
الحل: لا؛
c) استعمل صيغة الميل لتحديد ما إذا كان كل ضلعين متتالين متعامدين أم لا وضح اجابتك.
الحل: لا؛ ميل JK يساوي 0 وميل JM يساوي 2 إحداهما لا يساوي سالب معكوس الآخر.
30) رافعات: في الشكل المجاور: ABCD ,GDEF متوازيا أضلاع متطابقان.
a) حدد الزوايا التي تطابق وضح تبريرك.
الحل: الزوايا C، E، G إجابة ممكنة: لأن الزوايا المتقابلة في متوازي الأضلاع متطابقة.
لأن متوازيي الأضلاع متطابقان لأن الزوايا المتقابلة في متوازي الأضلاع متطابقة وتطابق حسب خاصية التعدي.
b) حدد القطع المستقيمة التي تطابق وضح تبريرك.
الحل:
لأن الأضلاع المتقابلة في متوازي الأضلاع متطابقة.
لأن متوازيي الأضلاع متطابقاً
لأن الأضلاع المتقابلة في متوازي الأضلاع متطابقة وتطابق حسب خاصية التعدي.
c) حدد الزوايا المكملة للزاوية C وضح تبريرك.
الحل:
الزوايا
مكملتان لأن الزوايا المتخالفة في متوازي الأضلاع متكاملة.
مكملة لأنها تطابق حسب نظرية الزوايا المتقابلة بالرأس ومكملة بالتعويض تطابق لأن الزوايا المتقابلة في متوازي الأضلاع متطابقة ومكملة -- بالتعويض.
31) تمثيلات متعددة: سوف تستقصي في هذه المسألة اختبارات لتمييز متوازي الأضلاع.
a) ارسم ثلاث من القطع المستقيمة المتطابقة والمتوازية صل الأطراف لتكون أشكالاً رباعية وسمها ABCD,MNOP,WXYZ ثم قس أطوال الأضلاع وقياسات الزوايا لكل منها.
b) جدولياً: أكمل الجدول الآتي:
| الشكل الرباعي | هل الاضلاع المتقابلة متطابقة؟ | هل الزوايا المتقابلة متطابقة؟ | هل الشكل متوازي أضلاع؟ |
| ABCD | نعم | نعم | نعم |
| MNOP | نعم | نعم | نعم |
| WXYZ | نعم | نعم | نعم |
C) لفظياً: ضع تخميناً حول الأشكال الرباعية التي لها ضلعان متطابقان ومتوازيان.
الحل: إذا كان في الشكل الرباعي ضلعان متوازيان ومتطابقان فإن هذا الشكل متوازي أضلاع.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)