تحقق من فهمك
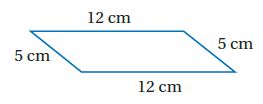
1A)
الحل:
نعم؛ لأن كل ضلعين متقابلين فيه متطابقان.
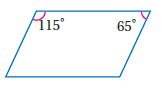
B2)
الحل:
لا؛ لأنه يحقق أي واحد من اختبارات متوازي الأضلاع.
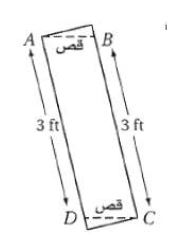
2) لوحات: عد إلى فقرة "لماذا"؟ بداية الدرس وضح لماذا يكون خطي القص أعلى وأسفل شريحة متوازيين.
الحل:
بما أن كل ضلعين متقابلين في الشكل الرباعي ABCD متطابقان فإن ABCD متوازي أضلاع إذن .
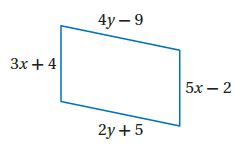
أوجد قمتي x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع.
3A)
الحل:
كل زاويتين متقابلتين متطابقين.
3B)
الحل:
مثل في المستوي الإحداثي الشكل الرباعي الذي أعطيت إحداثيات رؤوسه فيما يأتي وحدد ما إذا كان متوازي أضلاع أم لا برر إجابتك باستعمال الطريقة المحددة في السؤال:
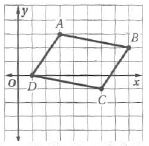
4A) صيغة المسافة.
الحل:
إذا كانت الأضلاع المتقابلة لشكل رباعي متطابقة فإنه متوازي أضلاع.
حيث أن المسافة بين نقطتين
بما أن لذلك فالشكل الرباعي ABCD متوازي أضلاع حسب النظرية 5.9
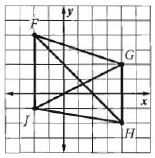
4B) صيغة نقطة المنتصف.
الحل:
إذا كان قطرا شكل رباعي ينصف كل منهما الآخر فإنه متوازي أضلاع وينصف قطرا شكل رباعي كل منهما الآخر إذا كانت نقطتا منتصفيهما متطابقتين.
نقطة منتصف القطر هي (1 , 1) ونقطة منتصف القطر هي (5, 0, 1).
حيث أن نقطة المنتصف .
وبما أن نقطتي منتصفي القطرين و ليس لهما الإحداثيات نفسها فإن الشكل الرباعي FGHJ ليس متوازي أضلاع.
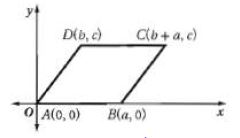
5) اكتب برهاناً احداثياً للعبارة الآتية: إذا كان الشكل الرباعي متوازي أضلاع فإن أضلاعه المتقابلة متطابقة.
الحل:
المعطيات: ABCD متوازي أضلاع.
المطلوب: AB=CD , AD = BC
برهان احداثي:
بما أن AB = DC وAD =BC فإن AB = DC وAD = BC.


.JPG)
.jpg)