مسائل مهارات التفكير العليا
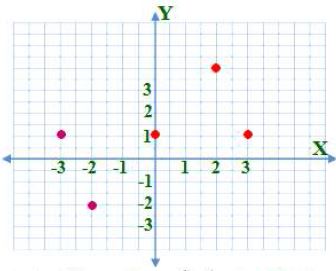
36) تحدٍ: يتقاطع قطرا متوازي أضلاع عند النقطة (1 ,0) ويقع أحد رؤوسه ند النقطة (2,4)، بينما يقع رأس آخر عند النقطة (3,1) أوجد موقعي الرأسين الآخرين.
الحل:
قطرا متوازي الأضلاع ينصف كل منهما الآخر.
(1 ,3-), (2- ,2-)
37) اكتب: بين أوجه الشبه والاختلاف بين النظريتين 1.9 و 1.3
الحل:
النظريتان إحداهما عكس الأخرى.
فرضية النظرية 1.3 "الشكل متوازي الأضلاع".
وفرضية النظرية 1.9 "الأضلاع المتقابلة في الشكل الرباعي متطابقة".
نتيجة النظرية 1.3 الأضلاع المتقابلة متطابقة ونتيجة النظرية 1.9 الشكل الرباعي متوازي أضلاع.
38) تبرير: إذا كانت الزوايا المتناظرة في متوازيي أضلاع متطابقة فهل يكون متوازيا الأضلاع متطابقين أحياناً أم دائماً أم لا يكونان متطابقين أبداً؟
الحل:
أحياناً يمكن أن يكون متوازي الأضلاع متطابقين ألا أنه يمكنك أيضاً جعل متوازي الأضلاع أكبر أو أصغر بتغيير أطوال الأضلاع ودون تغيير قياسات الزوايا.
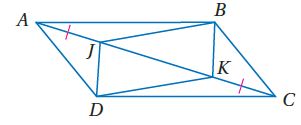
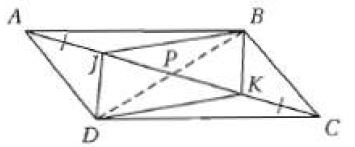
39) تحدٍ: في الشكل المجاور ABCD متوازي أضلاع بين أن الشكل الرباعي JBKD متوازي أضلاع.
الحل:
المعطيات: ABCD متوازي أضلاع و
المطلوب: JBKD متوازي أضلاع.
البرهان: ارسم
بما أن ABCD متوازي أضلاع فإن القطرين ينصف كل منهما الآخر حسب النظرية 1.7 سم نقطة تقاطعهما P ومن تعريف نقطة المنتصف يكون إذن AP = PC
وحسب مسلمة جمع القطع المستقيمة فإن:
وبالتعويض.
AJ + JP = PK + KC وبما أن فإن AJ = KC حسب تعريف التطابق KC + JP = PK + KC وبالتعويض KC + JP = PK + KC ومن خاصية الطرح يكون JP = PK.
إذن ومن تعريف التطابق تكون إذن P نقطة منتصف وبما أن تنصف كل منهما الأخرى وهما قطران للشكل الرباعي JBKD فحسب النظرية 1.11 يكون الشكل الرباعي JBKD متوازي أضلاع.
40) اكتب: استعمل العبارات الشرطية الثنائية "إذا وفقط إذا" في دمج كل من النظريات: 1.9 و1.10 و1.11 و1.12 وعكسها.
الحل:
يكون الشكل الرباعي متوازي أضلاع إذا أمكنك بيان أن:
كل ضلعين متقابلين متطابقين أو متوازيين.
أو كل زاويتين متقابلتين متطابقتين أو القطران ينصف كل منهما الآخر أو ضلعان متقابلان متطابقان ومتوازيان.
41) إذا كان الضلعان في الشكل الرباعي ABCD متوازيين فأي المعطيات الآتية كافية لإثبات أن ABCD متوازي أضلاع؟
الحل:
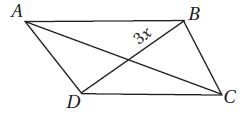
42) إجابة قصيرة: في الشكل الرباعي ABCD أدناه إذا كان تنصف فما قيمة x التي تجعل ABCD متوازي أضلاع؟
الحل:


.JPG)

.JPG)