حلول الأسئلة
السؤال
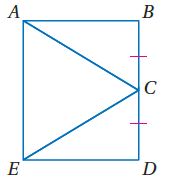
إذا كان ABDE مستطيلاً و فأثبت أن .
الحل
المعطيات: ABDE مستطيل،
- المطلوب:
- البرهان: العبارات (المبررات):
1) ABDE مستطيل (معطيات).
2) ABDE متوازي أضلاع (تعريف المستطيل).
3) (الأضلاع المتقاربة في متوازي الأضلاع متطابقة).
4) و قائمتان (تعريف المستطيل).
5) (جميع الزوايا القائمة متطابقان).
6) (SAS)
7) ( العناصر المتناظرة في المثلثين المتطابقين متطابقة).
مشاركة الحل
تأكد
.jpg)
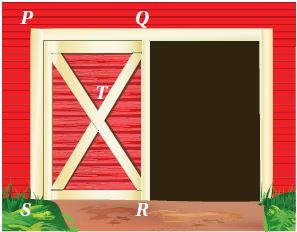
زراعة: الشكل المجاور يبين بوابة مخزن حبوب مستطيلة الشكل فيها الدعامتان المتقاطعتان تقويان دفة البوابة وتحفظانها من الالتواء مع مرور الزمن.
إذا كان فأوجد كلا مما يأتي:
1) QR
الحل: (الضلعان المتقابلان في المستطيل متطابقان).
PS =QR=7ft
2) SQ
الحل:
3)
الحل:
4)
الحل:
جبر: استعن بالمستطيل DEFG المبين جانباً.
5) إذا كان فأوجد EG.
الحل: قطرا المستطيل متطابقان.
6) إذا كان فأوجد
الحل:
7) برهان: إذا كان ABDE مستطيلاً و فأثبت أن .
الحل:
- المعطيات: ABDE مستطيل،
- المطلوب:
- البرهان: العبارات (المبررات):
1) ABDE مستطيل (معطيات).
2) ABDE متوازي أضلاع (تعريف المستطيل).
3) (الأضلاع المتقاربة في متوازي الأضلاع متطابقة).
4) و قائمتان (تعريف المستطيل).
5) (جميع الزوايا القائمة متطابقان).
6) (SAS)
7) ( العناصر المتناظرة في المثلثين المتطابقين متطابقة).
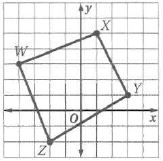
هندسة إحداثية: مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه في كل من السؤالين الآتيين وحدد ما إذا كان مستطيلاً أم لا برر إجابتك باستعمال الطريقة المحددة في السؤال.
8) , صيغة الميل.
الحل:
بما أن ميل لا يساوي ميل أي انهما غير متوازيان إذن WXYZ ليس متوازي أضلاع لذلك WXYZ ليس مستطيل.
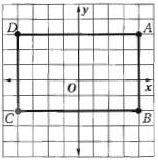
9) صيغة المسافة.
الحل:
بما أن AB = 5 = CD, BC = 8 = AD فإن ABCD متوازية أضلاع وبما أن فإن القطرين متطابقان لذلك فالشكل ABCD مستطيل.


.JPG)