حلول الأسئلة
السؤال
أضاف زيد رفاً جديداً لمكتبة ودعائم معدنية متقاطعة كما في الشكل المجاور كم يجب أن يكون طول كل من الدعائم المعدنية بحيث تكون الرفوف عمودية على الجانبين؟ وضح اجابتك. (إرشاد: ).
الحل
حتى تكون الزوايا قوائم يجب أن تكون أطوال الدعائم الحديدية متساوية وبما أن طول الرف معلوم والمسافة بين الرفوف معلومة فيمكن استعمال نظرية فيثاغورث لإيجاد طول الدعامة الحديدية وقد وجد أن طول الدعامة 3 أقدام و3 بوصات.
مشاركة الحل
تدرب وحل المسائل
سياج: سياج مستطيل الشكل تستعمل فيه دعائم متقاطعة السياج.
إذا كان فأوجد كلا مما يأتي:
10) BD
الحل:
BD = AC = 2ft
11) CB
الحل:
12)
الحل: قطرا المستطيل متطابقان وينصف كل منهما الآخر.
13)
الحل:
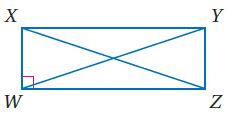
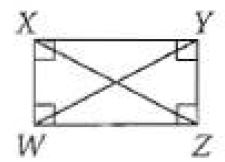
جبر: استعن بالمستطيل WXYZ المبين جانباً.
14) إذا كان ZY = 2x + 3 WX = x + 4 فأوجد WX.
الحل:
15) إذا كان PY = 3x – 5 , WP = 2x + 11 فأوجد ZP.
الحل:
16) إذا فأوجد .
الحل:
17) إذا كان ZP = 4x – 9 , PY = 2x + 5 فأوجد ZX.
الحل:
18)
الحل:
19)
الحل:
برهان: اكتب برهاناً ذا عمودين كل مما يأتي:
20) المعطيات: ABCD مستطيل.
المطلوب:
الحل:
البرهان: العبارات (المبررات):
1) ABCD مستطيل (معطى).
2) ABCD متوازي أضلاع (تعريف المستطيل).
3) (الأضلاع المتقابلة لمتوازي الأضلاع متطابقة).
4) ( خاصية الانعكاس).
5) ( قطرا المستطيل متطابقان).
6) (SSS)
21) المعطيات: QTVW مستطيل.
المطلوب:
الحل:
البرهان: العبارات (المبررات):
1)
4) قائمتان. (تعريف المستطيل).
5) (جميع الزوايا القائمة متطابقة).
6) QR = ST (تعريف تطابق القطع المستقيمة).
7) (خاصية الانعكاس).
8) RS = RS (تعريف تطابق القطع المستقيمة).
9) QR + RS = RS + ST (خاصية الإضافة).
10) QS = QR + RS , RT = RS + ST (مسلمة جمع القطع المستقيمة).
11) QS = RT (بالتعويض).
12) ( تعريف تطابق القطع المستقيمة).
13) (SAS)
هندسة إحداثية: مثل في المستوى الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي وحدد ما إذا كان مستطيلاً أم لا برر إجابتك باستعمال الطريقة المحددة في السؤال.
22) W(-2, 4), X(5, 5), Y(6, -2), Z(-1, -3) صيغة الميل.
الحل:
نعم؛ بما أن ميل يساوي ميل ويساوي 7, وميل يساوي ميل ويساويفإن WXYZ متوازي أضلاع وبما أن حاصل ضرب ميلي كل ضلعين متجاورين يساوي 1-فإن الأضلاع المتجاورة متعامدة وتشكل زوايا قائمة لذلك فالشكل WXYZ مستطيل.
23) J(3,3), K(-5,2), L(-4,-4), M(4,-3), صيغة المسافة بين نقطتين.
الحل:
بما أن JK = LM , KL = MJ فإن QRST متوازي أضلاع.
وبما أن فإن القطرين متطابقان إذن فالشكل QRST مستطيل.
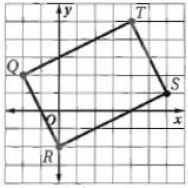
24) Q (-2,2), R(0,-2), S(6,1), T(4,5) صيغة المسافة بين نقطتين.
الحل:
بما أن QR = ST, RS = TQ فإن QRST متوازي أضلاع.
وبما أن فإن القطرين متطابقان إذن فالشكل QRST مستطيل.
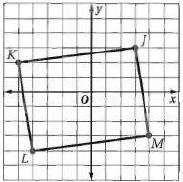
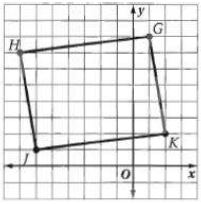
25) G(1,8), H(-7,7), J(-6,1), K(2,2) صيغة الميل.
الحل:
نعم؛ بما أن ميل يساوي ميل ويساوي وميل يساوي ميل ويساوي 8 فإن GHJK متوازي أضلاع وبما أن حاصل ضرب ميلي كل ضلعين متجاورين لا يساوي 1- فإن الأضلاع المتجاورة ليست متعامدة ولا تشكل زوايا قائمة لذلك فالشكل WXYZ ليس مستطيل.
في المستطيل ABCD إذا كان
فأوجد كلا مما يأتي:
26)
الحل:
27)
الحل:
28)
الحل:
29)
الحل:
30)
الحل:
مثلث متطابق الضلعين
31)
الحل:
32) مكتبات: أضاف زيد رفاً جديداً لمكتبة ودعائم معدنية متقاطعة كما في الشكل المجاور كم يجب أن يكون طول كل من الدعائم المعدنية بحيث تكون الرفوف عمودية على الجانبين؟ وضح اجابتك. (إرشاد: ).
الحل:
حتى تكون الزوايا قوائم يجب أن تكون أطوال الدعائم الحديدية متساوية وبما أن طول الرف معلوم والمسافة بين الرفوف معلومة فيمكن استعمال نظرية فيثاغورث لإيجاد طول الدعامة الحديدية وقد وجد أن طول الدعامة 3 أقدام و3 بوصات.
برهان: اكتب برهاناً ذا عمودين لإثبات النظيرة في كل من السؤالين الآتيين:
33) النظرية 1.13
الحل:
المعطيات: WXYZ مستطيل قطراه و
المطلوب:
البرهان:
1) WXYZ مستطيل قطراه XZ وWY (معطيات).
2) (الأضلاع المتقابلة للمستطيل متطابقة).
3) (خاصية الانعكاس).
4) قائمتان (تعريف المستطيل).
5) (جميع الزوايا القائمة متطابقة).
6) (SAS)
7) (العناصر المتناظرة في المثلثين المتطابقين متطابقة).
34) النظرية 1.14
الحل:
المعطيات: WXYZ متوازي أضلاع و
المطلوب: WXYZ مستطيل.
البرهان:
1) WXYZ متوازي أضلاع و (معطيات).
2) (كل ضلعين متقابلين في متوازي الأضلاع متطابقان).
3)
4) (العناصر المتناظرة في مثلثين متطابقين متطابقة).
5) (تعريف الزوايا المتطابقة).
6) متكاملتان (الزوايا المتحالفة في متوازي الأضلاع متكاملة).
7)
(تعريف الزاويتين المتكاملتين).
8) قائمتان (إذا كانت زاويتان متطابقتين ومتكاملتين فإن كلاً منهما قائمة).
9) قائمتان (إذا كانت احدى زوايا متوازي أضلاع قائمة فإن زواياه الأربع قائمة).
10) WXYZ مستطيل (تعريف المستطيل).
35) رياضة: قام سلمان بعمل التخطيط الخارجي لملعب كرة قدم وضح كيف يمكنه التحقق من أن الملعب مستطيل الشكل باستعمال شريط القياس فقط.
الحل:
يجب أن يقيس قطري الملعب والأضلاع فإذا كان القطران متطابقين وكل ضلعين متقابلين متطابقين فإن الملعب مستطيل الشكل.
36) تمثيلات متعددة: سوف تستقصي في هذه المسألة خصائص متوازيات أضلاع خاصة.
a) هندسياً: ارسم ثلاث متوازيات أضلاع كل منها أضلاعه الأربعة متطابقة وسمها ABCD, MNOP, WXYZ ثم ارسم قطري كل منها وسم نقطة تقاطعهما R.
الحل:

b) جدولياً: استعمل المنقلة لقياس الزوايا وأكمل الجدول الآتي.
| متوازي أضلاع | ABCD | MNOP | WXYZ | |||
| الزوايا | ||||||
| قياس الزاوية | 90º | 90º | 90º | 90º | 90º | 90º |
c) لفظياً: اكتب تخميناً حول قطري متوازي الأضلاع المتطابق الأضلاع.
الحل:
إذا كانت الأضلاع الأربعة في متوازي الأضلاع متطابقة فإن قطريه متعامدان.
جبر: استعن بالمستطيل WXYZ المبيَّن جانباً.
37) إذا كان XW = 3, WZ = 4 فأوجد YW.
الحل:
38) إذا كان ZY = 6, XY = 8 فأوجد W.
الحل:

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)