يلعب بندر بلوحة تتطلب رمي مكعبي أرقام حيث يحتاج إلى الحصول على المجموع ٦ في الرمية الأولى والمجموع ١٠ في الرمية الثانية للحصول على مربعات إضافية فما احتمال أن يحصل بندر على المجموع ٦ ثم المجموع ١٠؟

احتمال أن يحصل على بندر على المجموع ٦ ثم المجموع ١٠ = $\frac{\mathrm{٥}}{\mathrm{٤٣٢}}$

حل أسئلة تدرب وحل المسائل

عند رمي مكعب أرقام، وسحب كرة من الكيس المجاور، أوجد احتمال كل مما يأتي:

٦- ح (١ وأحمر).

ح (١ وأحمر) = $\frac{\mathrm{١}}{\mathrm{٦}}\times \frac{\mathrm{٢}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{٢٤}}$

٧- ح (٣ وبنفسجي).

ح (٣ وبنفسجي) = $\frac{\mathrm{١}}{\mathrm{٦}}\times \frac{\mathrm{١}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{٤٨}}$

٨- ح (زوجي وأصفر).

ح (زوجي وأصفر) = $\frac{\mathrm{٣}}{\mathrm{٦}}\times \frac{\mathrm{٢}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{٨}}$

٩- ح (فردي وليس أخضر).

ح (فردي وليس أخضر) = $\frac{\mathrm{٣}}{\mathrm{٦}}\times \frac{\mathrm{٦}}{\mathrm{٨}}=\frac{\mathrm{٣}}{\mathrm{٨}}$

١٠- ح (أقل من ٤ وأزرق).

ح (أقل من ٤ وأزرق) = $\frac{\mathrm{٣}}{\mathrm{٦}}\times \frac{\mathrm{١}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{١٦}}$

١١- ح (أكبر من ١ وأحمر).

ح (أكبر من ١ وأحمر) = $\frac{\mathrm{٥}}{\mathrm{٦}}\times \frac{\mathrm{٢}}{\mathrm{٨}}=\frac{\mathrm{٥}}{\mathrm{٢٤}}$

١٢- غسيل: تحتوي سلة غسيل على ١٨ جورباً أزرق اللون و٢٤ جورباً أسود فما احتمال سحب جوربين بلون أسود واحداً تلو الآخر من السلة؟

ح (جوربان أسود) = ح (الجورب الأول) × ح (الجورب الثاني).

= $\frac{\mathrm{٢٤}}{\mathrm{٤٢}}\times \frac{\mathrm{٢٣}}{\mathrm{٤١}}=\frac{\mathrm{٥٥٢}}{\mathrm{١٧٢٢}}=\frac{\mathrm{٩٢}}{\mathrm{٢٨٧}}$

١٣- ألعاب: يلعب بندر بلوحة تتطلب رمي مكعبي أرقام حيث يحتاج إلى الحصول على المجموع ٦ في الرمية الأولى والمجموع ١٠ في الرمية الثانية للحصول على مربعات إضافية فما احتمال أن يحصل بندر على المجموع ٦ ثم المجموع ١٠؟

احتمال أن يحصل على بندر على المجموع ٦ ثم المجموع ١٠ = $\frac{\mathrm{٥}}{\mathrm{٤٣٢}}$

يوضح الجدول المجاور ألوان الملابس الرياضية لطلاب أحد الفصول فإذا اختير طالبان عشوائياً فأوجد احتمال كل مما يأتي:

١٤- ح (ملابسهما زرقاء).

ح (ملابسهما زرقاء) = $\frac{\mathrm{١}}{\mathrm{١٩}}$

١٥- ح (أخضر ثم أصفر).

ح (أخضر ثم أصفر) = $\frac{\mathrm{٥}}{\mathrm{٢٠}}\times \frac{\mathrm{٧}}{\mathrm{١٩}}=\frac{\mathrm{٧}}{\mathrm{٧٦}}$

١٦- ح (أحمر ثم أزرق).

ح (أحمر ثم أزرق) = $\frac{\mathrm{٤}}{\mathrm{٢٠}}\times \frac{\mathrm{٥}}{\mathrm{١٩}}=\frac{\mathrm{١}}{\mathrm{١٩}}$

١٧- ح (أصفر ثم أزرق).

ح (أصفر ثم أزرق) = $\frac{\mathrm{٧}}{\mathrm{٢٠}}\times \frac{\mathrm{٥}}{\mathrm{١٩}}=\frac{\mathrm{٧}}{\mathrm{٧٦}}$

١٨- ح (ملابسهما خضراء).

ح (ملابسهما خضراء) = $\frac{\mathrm{٣}}{\mathrm{٩٥}}$

١٩- ح (ملابسهما ليست حمراء).

ح (ملابسهما ليست حمراء) = $\frac{\mathrm{١٢}}{\mathrm{١٩}}$

مدارس: إذا علمت أن ٥٦٪ من طلاب إحدى المدارس يمارسون رياضة المشي و٤٤٪ لا يمارسونها فاستعمل المعلومات في الجدول المجاور لحل السؤالين ٢٠ - ٢١:

٢٠- إذا اختير طالبان عشوائياً فما احتمال أن يكون الطالب الأول ممارساً رياضة المشي وأن يفضل الطالب الثاني مادة العلوم؟

ح (الطالب الأول يفضل المشي) × ح (الطالب الثاني يفضل العلوم).

$\frac{\mathrm{٥٦}}{\mathrm{١٠٠}}\times \frac{\mathrm{٢١}}{\mathrm{١٠٠}}=\frac{\mathrm{١١٧٦}}{\mathrm{١٠٠٠٠}}= \mathrm{١١٧٦}.\mathrm{٠}=$١١.٧٦

٢١- ما احتمال أن يكون الطالب الأول لا يمارس رياضة المشي وألا يفضل الطالب الثاني مادة اللغة الإنجليزية ولا مادة الرياضيات؟

ح (الطالب الأول غير ممارس المشي) × ح (الطالب الثاني لا يفضل الإنجليزية ولا الرياضيات).

$\frac{\mathrm{٤٤}}{\mathrm{١٠٠}}\times \frac{\mathrm{٥٦}}{\mathrm{١٠٠}}=\frac{\mathrm{٢٤٦٤}}{\mathrm{١٠٠٠٠}}$ = ٠.٢٤٦٤ = ٢٤.٦٤

٢٢- كتب: قرر طارق وصديقه قراءة كتاب من بين ٦ كتب أدبية و٤ دينية و٣ شعرية وكتابي تاريخ وكتاب علمي فكتبنا عناوين هذه الكتب على قصاصات ورقية ووضعاها في صندوق ثم اختار كل منهما كتاباً بصورة عشوائية فما احتمال ألا يختار أي منهما كتاباً أدبياً؟ وهل هذه الحادثة مستقلة أم غير مستقلة؟ وضح إجابتك.

ح (لا يختار الاثنان كتاب أدبي) = $\frac{\mathrm{١٠}}{\mathrm{١٦}}\times \frac{\mathrm{٩}}{\mathrm{١٥}}=\frac{\mathrm{٣}}{\mathrm{٨}}$

الحد ص غير مستقل فبعد اختيار القصاصة الأولى يقل عدد القصاصات في الصندوق واحد.

٢٣ - تسوق: وجد بقال إن ٦٠٪ من زبائنه ينفق كل منهم أكثر من ٧٥ ريالاً في كل زيارة فإذا اشترى شخصان منه فما احتمال أن ينفق كلاهما أكثر من ٧٥ ريالاً؟

ح (أن ينفق كل منهما أكثر من ٧٥ ريال) = ٣٦٪.

٢٤- نقود: لدى هالة ٨ قطع معدنية من فئة ((نصف ريال)) و٦ قطع معدنية من فئة ((الريال)) فإذا سحبت إحدى القطع دون إرجاعها ثم سحبت قطعة ثانية فما احتمال أن تكون القطعتان من فئة ((نصف ريال))؟ وهل الحادثتان مستقلتان أم لا؟ وضح ذلك.

ح (أن تكون القطعتان من فئة نصف ريال) = $\frac{\mathrm{١٤}}{\mathrm{١٣}}$ والحدث هنا غير مستقل لأن القطعة الأولى لم ترجع.

٢٥- مسابقات: يربح أحد المتسابقين العشرة سيارة جديدة عن طريق اختيار المفتاح الرابح عشوائياً من بين عشرة مفاتيح أوجد احتمال ألا يسحب أول ثلاثة متسابقين المفتاح الرابح.

ح (ألا يسحب أول متسابقين المفتاح الرابح) = $\frac{\mathrm{٧}}{\mathrm{١٠}}$

٢٦- دومينو: تتألف مجموعة الدومينو الاعتيادية من ٢٨ قطعة كل قطعة منها مكونة من جزأين يحمل كل منهما نقاطاً من (٠ - ٦). فإذا كان ٧ من هذه القطع تحمل الرقم نفسه على الوجهين واختار ٤ لاعبين قطعة عشوائياً فما احتمال أن يختار كل منهم قطعة لها العدد نفسه من النقاط على الجزأين؟

ح (أن يختار كل منهم حجراً له العدد نفسه من النقاط على الوجهين) = $\frac{\mathrm{٧}}{\mathrm{٢٨}}\times \frac{\mathrm{٦}}{\mathrm{٢٨}}\times \frac{\mathrm{٥}}{\mathrm{٢٦}}\times \frac{\mathrm{٤}}{\mathrm{٢٥}}=\frac{\mathrm{١}}{\mathrm{٥٨٥}}$

٢٧- طقس: توقعت الهيئة العامة للأرصاد أن فرصة هطول الأمطار يوم الاثنين هي ٨٠٪ وأن فرصة هطول الأمطار يوم الثلاثاء هي ٣٠٪ أوجد احتمال هطول الأمطار يومي الإثنين والثلاثاء؟ افرض أن الحادثتين مستقلتان.

بما أن الحدثين مستقلان إذن ح (الاثنين والثلاثاء).

= $\frac{\mathrm{٨٠}}{\mathrm{١٠٠}}\times \frac{\mathrm{٣٠}}{\mathrm{١٠٠}}=\frac{\mathrm{٢٤}}{\mathrm{١٠٠}}$= ٢٤٪

٢٨- مسألة مفتوحة: يوجد في صندوق ٩ كرات بثلاثة ألوان مختلفة اكتب مسألة تتعلق بسحب كرتين عشوائياً دون إرجاعهما إلى الصندوق على أن يكون الاحتمال $\frac{\mathrm{١}}{\mathrm{٦}}$.

يوجد في صندوق ٤ كرات حمراء و٣ خضراء وكرتان زرقاوان، إذا تم سحب كرتين عشوائياً دون إرجاع فاحتمال أن تكون الكرتان حمراوين هو $\frac{\mathrm{٤}}{\mathrm{٩}}\times \frac{\mathrm{٣}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{٦}}$

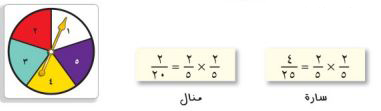
٢٩- اكتشف الخطأ: تم تدوير القرص الدوار المجاور مرتين وحسبت كل من منال وسارة احتمال أن يقف المؤشر على عدد زوجي في المرتين فأيهما كانت على صواب؟ وضح إجابتك.

سارة هي الصحيح لأن تدوير القرص الدوار مرتين يمثل حادثين مستقلين احتمال الحصول على عدد زوجي في كل مرة $\frac{\mathrm{٢}}{\mathrm{٥}}$

٣٠- تحد: حدد ما إذا كانت الجملة الآتية صحيحة أم خاطئة وإذا كانت خاطئة فأعط مثالاً مضاداً: ((إذا كانت الحادثتان مستقلتين، فإن احتمالهما معاً أقل من ١)).

خطأ؛ احتمال ظهور أو كتابة عند رمي قطعة نقد وظهور العدد ستة أو أقل عند رمي مكعب الأرقام.

٣١- اكتب: ما الفرق بين الحادثتين المستقلتين وغير المستقلتين؟

كل من الحوادث المستقلة وغير المستقلة هي حوادث مركبة، الحوادث المستقلة لا يتأثر بعضها ببعض في حين تتأثر الحوادث غير المستقلة.

٣٢- أربع بطاقات كتب عليها الأرقام ١، ٢، ٣، ٤. إذا سحب عبد الله بطاقة منها بشكل عشوائي واحتفظ بها ثم سحب سعد بطاقة أخرى فما احتمال أن تحمل بطاقة سعد الرقم ٢ علماً بأن البطاقة التي سحبها عبد الله تحمل الرقم ٤؟

أ. $\frac{\mathrm{١}}{\mathrm{٢}}$

ب. $\frac{\mathbf{١}}{\mathbf{٣}}$

جـ. $\frac{\mathrm{١}}{\mathrm{٤}}$

د. $\frac{\mathrm{١}}{\mathrm{٥}}$

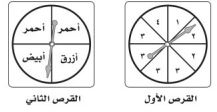
٣٣- ‌أدار أحمد كلاً من مؤشري القرصين أدناه ما احتمال أن يقف مؤشر القرص الأول على العدد ٢ ومؤشر القرص الثاني على اللون الأبيض؟

أ. $\frac{\mathbf{١}}{\mathbf{١٦}}$

ب. $\frac{\mathrm{١}}{\mathrm{٤}}$

جـ. $\frac{\mathrm{٢}}{\mathrm{٥}}$

د. $\frac{\mathrm{٣}}{\mathrm{٥}}$

احتمال أن يقف المؤشر على العدد ٢ هو $\frac{\mathrm{٢}}{\mathrm{٨}}=\frac{\mathrm{١}}{\mathrm{٤}}$

ومؤشر القرص الثاني على اللون الأبيض هو $\frac{\mathrm{١}}{\mathrm{٤}}$

$\frac{\mathrm{١}}{\mathrm{٤}}$ × $\frac{\mathrm{١}}{\mathrm{٤}}$ = $\frac{\mathrm{١}}{\mathrm{١٦}}$