أوجد قياس الزاوية في كل مضلع مما يأتي إذا علمت أنها جميعاً منتظمة وقربه إلى أقرب عشر: تساعي.

نقسم الشكل إلى ٧ مثلثات.

بما أن مجموع زوايا المثلث = ١٨٠°

مجموع زوايا الشكل التساعي = ٧ × ١٨٠ = ١٢٦٠°

قياس الزوايا في الشكل التساعي =

٩ ن = ١٢٦٠

ن = ١٤٠°

حل أسئلة تدرب وحل المسائل

أي الأشكال الآتية مضلع؟ وهل هو منتظم أم لا؟ وإذا كان مضلعاً فصنفه وإذا لم يكن مضلعاً فاذكر السبب:

٧-

بما أن به ضلعين متقاطعين، ليس مضلعاً.

٨-

الشكل يتكون من ٨ أضلاع متطابقة الشكل ثماني منتظم.

٩-

الشكل يتكون من ٣ أضلاع مغلقة الشكل مثلث قائم الزاوية متطابق الضلعين، وليس منتظماً.

١٠-

الشكل به ضلع منحني وليس مستقيم الشكل ليس مضلعاً.

١١-

الشكل يتكون من قطع مستقيمة مختلفة الشكل مضلع غير منتظم.

١٢-

الشكل عبارة عن ١٠ أضلاع متطابقة الشكل مضلع عشاري منتظم.

أوجد قياس الزاوية في كل مضلع مما يأتي إذا علمت أنها جميعاً منتظمة وقربه إلى أقرب عشر:

١٣- عشاري.

نقسم العشاري إلى ٨ مثلثات.

بما أن مجموع زوايا المثلث = ١٨٠°

مجموع زوايا العشاري = ٨ × ١٨٠ = ١٤٤٠°

قياس الزوايا = ١٤٤٠ ÷ ١٠ = ١٤٤°

١٠ ن = ١٤٤٠

ن = ١٤٤°

١٤- تساعي.

نقسم الشكل إلى ٧ مثلثات.

بما أن مجموع زوايا المثلث = ١٨٠°

مجموع زوايا الشكل التساعي = ٧ × ١٨٠ = ١٢٦٠°

قياس الزوايا في الشكل التساعي =

٩ ن = ١٢٦٠

ن = ١٤٠°

١٥- رباعي.

نقسم الرباعي إلى مثلثين.

بما أن مجموع زوايا المثلث = ١٨٠°

مجموع زوايا الرباعي = ٢ × ١٨٠ = ٣٦٠°

٤ ن = ٣٦٠

ن = ٩٠°

١٦- ١١ ضلعاً.

س = $\frac{(ع -\mathrm{٢}) \times \mathrm{١٨٠}}{ع}=\frac{\mathrm{٩} \times \mathrm{١٨٠}}{\mathrm{١١}}$= ١٤٧,٣°

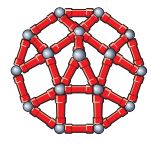
١٧- ألعاب: يستعمل عمر مجموعة القطع الممغنطة ليصنع مضلعاً عشارياً كما في الشكل فإذا كان معه تكفي لصنع عدة عشارياً كما في الشكل فإذا كان معه قطع تكفي لصنع عدة مضلعات عشارية فهل يمكن ترتيبها لتشكل تبليطاً؟ وضح إجابتك.

بما أن في التبليط يلزم أن يكون مجموع الزوايا الملتقية ٣٦٠°

وزاوية الشكل الرباعي = ١٤٤°

٣٦٠ لا تقبل القسمة على ١٤٤ وينتج عنها باقي إذاً لا يمكن التبليط بها.

صنف المضلعات المستعملة في كل تبليط مما يأتي:

١٨-

سداسي، مثلث.

١٩-

سداسي، مربع، مثلث.

٢٠-

ثماني، مربع.

٢ ١- ما محيط مضلع تساعي منتظم طول ضلعه ٤,٨ سم؟

التساعي به ٩ أضلاع، المحيط مجموع أطوال الأضلاع.

محيط التساعي = طول الضلع × ٩

= ٤,٨ × ٩ = ٤٣,٢ سم.

٢ ٢- ما محيط مضلع خماسي منتظم طول ضلعه $\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{٧}$ سم؟

الخماسي مكون من ٥ أضلاع.

محيطه = طول الضلع × ٥

= $\frac{\mathrm{٧}}{\mathrm{٤}}$ × ٥ = ٣٦,٢٥ سم.

٢٣- فنون: الصورة المجاورة هي أرضية أحد القصور التاريخية سم المضلعات الموجودة في هذه الأرضية.

مربع، شبه منحرف، متوازي أضلاع.

٢٤- إشارة مرور: يظهر في الشكل المجاور إحدى إشارات المرور المصنوعة من صفيحة معدنية هل يمكن تقسيم الصفيحة المعدنية لصنع تسع إشارات مشابهة بحيث لا يبقى أي جزء من الصفيحة المعدنية؟ وضح إجابتك.

لا، إشارة قف هي شكل ثماني ولا يمكن استعماله في التبليط. لذا سيكون هناك فولاذ زائد بعد قص ٩ إشارات منها.

٢٥- بحث: استعمل الشبكة المعلوماتية أو أي مصدر آخر لمعرفة إشارات المرور الأخرى وسم نوعها وشكلها وبين ما إذا كان شكلها منتظماً أم لا.

يوجد عدة إشارات منها ما هو على شكل مثلث منتظم ومنها ما هو على شكل سداسي منتظم.

٢٦- تبرير: صح أم خطأ؟ يمكن تبليط المستوى فقط بمضلع منتظم. وضح إجابتك.

هذه الجملة خطأ.

٢٧- مسألة مفتوحة: ارسم أمثلة حياتية لمضلعين خماسي وسداسي.

٢٨- تحد: يمكن التبليط بمثلثات متطابقة الأضلاع فهل يمكن التبليط بمثلثات مختلفة الأضلاع.

نعم، مجموع قياسات زوايا أي مثلث ١٨٠°

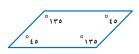
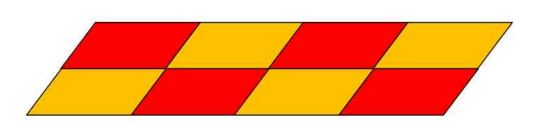
٢٩- اكتب: في الشكل المجاور متوازي أضلاع وضح كيف يمكنك استعماله في التبليط.

٣٠- أي جملة مما يأتي ليست صحيحة عن المضلعات؟

أ. يصنف المضلع وفقاً لعدد أضلاعه.

ب. يتقاطع كل ضلع في المضلع مع أضلاعه الأخرى جميعها.

جـ. يتكون المضلع من ٣ قطع مستقيمة أو أكثر.

د. تتلاقى القطع المستقيمة التي يتكون منها المضلع عند نهاياتها فقط.

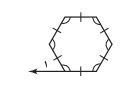
٣١- إجابة قصيرة: ما قياس الزاوية ١ في الشكل أدناه؟

بما أن الشكل السداسي منتظم.

إذن كل زوايا متساوية = ١٢٠°

E ق µ ١= ١٨٠ - ١٢٠ = ٦٠°