حل أسئلة اختبار الفصل السابع
سم كلاً من الزاويتين الآتيتين بأربع طرائق، ثم صنفها إلى زاوية حادة أو منفرجة أو قائمة:
١- .JPG)
µ أ ب جـ أو µ جـ ب أ أو µ ب أو µ ٢
بما أن قياسها أكبر من ٩٠° وأقل من ١٨٠°
الزاوية منفرجة.
٢- .JPG)
µ س ص ع أو µ ع ص س أو µ ص أو µ ١
بما أن قياسها اقل من ٩٠°
الزاوية حادة.
صنف كل زوج من الزوايا الآتية إلى متكاملة أو متتامة أو غير ذلك:
٣- 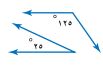
مجموع الزاويتين = ١٢٥ + ٢٥ = ١٥٠°
الزاويتين غبر متكاملتين وغير متتامتان.
٤- 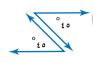
مجموع الزاويتين = ٤٥ + ٤٥ = ٩٠°
إذا الزاويتين متتامتين.
٥- هندسة: صنف زوج الزوايا المجاور إلى متقابلة بالرأس أو متجاورة أو غير ذلك.
الزاويتين متجاورتين.
٦- اختيار من متعدد: يبين الجدول الآتي نتائج مسح، يراد تمثيلها بالقطاعات الدائرية، أي الجمل الآتية غير صحيحة بخصوص التمثيل؟
| الكعك المفضل | |
| النوع | الطلاب |
| كعكة الفواكه | ٨ |
| كعكة الزبيب | ٩ |
| كعكة القرفة | ١٨ |
| الكعكة العادية | ٣٢ |
أ. اختار ١٢٪ من الطلاب تقريباً كعكة الفواكه.
ب. قياس زاوية القطاع الذي يمثل كعكة الفواكه ٤٣°
جـ. زاويتا قطاع كعكة القرفة، وقطاع الكعكة العادية متتامتان.
د. يفضل الطلاب الكعكة العادية أكثر من أي نوع آخر.
قياس زاوية كعكة القرفة في القطاع = ٣٦٠ × ١٨٪ = ٣٦٠ × ٠,١٨
= ٦٤,٨°
قياس زاوية الكعكة العادية في القطاع = ٣٦٠ × ٣٢٪ = ٣٦٠ × ٠,٣٢
= ٨٥,٢°
مجموع الزاويتين = ٦٤,٨ + ٨٥,٢ = ١٨٠°
إذا الزاويتان متكاملتين وليس متتامتين، إذن الإجابة الصحيحة جـ.
جبر: أوجد القياس المجهول في كل مثلث مما يأتي:
٧- ٧٥°، ٥, ٢٥°، س°
بما أن مجموع زوايا المثلث = ١٨٠°
٧٥ + ٢٥,٥ + س = ١٨٠
س + ١٠٠,٥ = ١٨٠
س = ٧٩,٥°
٨- ٢٣,٥°، س°، ١٠٩,٥°
بما أن مجموع زوايا المثلث = ١٨٠°
٢٣,٥ + ١٠٩,٥ + س = ١٨٠
س + ١٣٣ = ١٨٠
س = ٤٧°
٩- جبر: تقبل الأعداد التي آحادها ٥ أو صفر القسمة على ٥ دون باق هل تقبل الأعداد ٢٥، ٨٩٣، ٦٩٠ القسمة على ٥ دون باق؟ استعمل طريقة التبرير المنطقي.
أفهم: الأعداد التي آحادها ٥ أو صفر تقبل القسمة على ٥ دون باق هل تقبل الأعداد ٢٥، ٨٩٣، ٦٩٠ القسمة على ٥ دون باق؟
خطط: استعمل التبرير المنطقي للإجابة.
حل: بما أن العدد ٢٥ آحاده ٥، إذاً يقبل القسمة على ٥ بدون باق.
بما أن العدد ٧٩٣ آحاده ٣ وليس ٥ أو صفر،
إذاً لا يقبل القسمة على ٥ باق.
بما أن العدد ٦٩٠ آحاده صفر إذاً يقبل القسمة على ٥ بدون باقي.
تحقق: اقسم كل منهم على ٥.
نجد أن العددين ٢٥، ٦٩٠ يقبل القسمة على ٥ دون باق.
والعدد ٧٩٣ يقسم على ٥ ويوجد باق.
جبر: أوجد قيمة س في الشكلين الرباعيين الآتيين:
١٠- 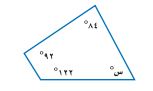
بما أن مجموع زوايا الشكل الرباعي = ٣٦٠°
٨٤ + ٩٢ + ١٢٢ + س = ٣٦٠
س + ٢٩٨ = ٣٦٠
س = ٦٢°
١١- 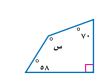
بما أن مجموع زوايا الشكل الرباعي = ٣٦٠°
٧٠ + ٩٠ + ٥٨ + س = ٣٦٠°
س + ٢١٨ = ٣٦٠
س = ١٤٢°
١٢- فنون: تم تكبير رسم بحيث يصبح طوله ٣٥ سم، وعرضه ٢٥سم، فإذا كان طوله الأصلي ٢٠ سم، فما عرضه الأصلي؟
بما أن الشكلين متشابهين.
٣٥ س = ٢٥ × ٢٠
٣٥س = ٥٠٠
س = ١٤,٢ سم
١٣- هندسة: هل يمكن استعمال شكل رباعي سباعي منتظم مجموع قياسات زواياه ٩٠٠° في عملية التبليط؟
لا، لا يمكن.
١٤- اختيار من متعدد: أي الأشكال الرباعية الآتية ليس فيه أضلاع متقابلة ومتطابقة؟
أ. متوازي الأضلاع.
ب. شبه المحرف.
جـ. المربع.
د. المستطيل.

.JPG)
.JPG)