صنِّف المثلث المشار إليه في كل من الأشكال الآتية من حيث الزوايا والأضلاع:

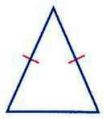
٦) بما أن جميع زواياه أقل من ٩٠$°$ وأضلاعه متساوية، مثلث متطابق الأضلاع وحاد الزوايا.

٧) بما أن المثلث به زاوية قائمة وأضلاعه مختلفة في الطول، مثلث قائم الزاوية ومختلف الأضلاع.

٨) بما أن جميع زواياه أقل من ٩٠$°$ وبه ضلعين متساويين، مثلث متطابق الضلعين وحاد الزوايا.

حل اسئلة تأكد

المثال١: أوجد قيمة س في كل مما يأتي:

١)

بما أن مجموع زوايا المثلث = ١٨٠°

س + ٦١ + ٧٥ = ١٨٠° اجمع الزاويتين.

س + ١٣٦ = ١٨٠° اطرح ١٣٦ من الطرفين.

س = ٤٤°

٢)

بما أن مجموع زوايا المثلث = ١٨٠°

س + ١٩ + ٢٧ = ١٨٠° اجمع الزاويتين.

س + ٤٦ = ١٨٠° اطرح ٤٦ من الطرفين.

س = ١٣٤°

٣)

بما أن مجموع زوايا المثلث = ١٨٠°

س + ٩٠ + ٤٥ = ١٨٠° اجمع الزاويتين.

س + ١٣٥ = ١٨٠° اطرح ١٣٥ من الطرفين.

س = ٤٥°

٤) جبر: أوجد ق$\angle$ع في $△$س ص ع، إذا كان ق$\angle$س = ٣٧° و ق$\angle$ص = ٥٥°.

بما أن مجموع زوايا المثلث = ١٨٠°

U ع + U س + U ص = ١٨٠

U ع + ٣٧ + ٥٥ = ١٨٠

U ع + ٩٢ = ١٨٠

U ع = ٨٨°

المثال٢: ٥) اختيار من متعدد: يستعمل المثلث المجاور في لعبة البلياردو أوجد قياس الزاوية المجهولة في المثلث.

أ) ٣٠°

ب) ٤٠°

جـ) ٦٠°

د) ٧٥°

قياس الزاوية المجهولة ج) ٦٠°

بما أن مجموع زوايا المثلث = ١٨٠°

س + ٦٠ + ٦٠ = ١٨٠

س + ١٢٠ = ١٨٠ بطرح ١٢٠ من الطرفين.

س = ٦٠°

المثال٣ طبيعة: صنف المثلث المشار إليه في كل من الأشكال الآتية من حيث الزوايا والأضلاع:

٦) بما أن جميع زواياه أقل من ٩٠° وأضلاعه متساوية، مثلث متطابق الأضلاع وحاد الزوايا.

٧) بما أن المثلث به زاوية قائمة وأضلاعه مختلفة في الطول، مثلث قائم الزاوية ومختلف الأضلاع.

٨) بما أن جميع زواياه أقل من ٩٠° وبه ضلعين متساويين، مثلث متطابق الضلعين وحاد الزوايا.

المثالان٤، ٥ رسم مثلثات: في كل من السؤالين ٩، ١٠، ارسم المثلث ثم صنفه:

٩) مثلث فيه ثلاث زوايا حادة، وضلعان متطابقان.

ارسم ضلعين متساويين بينها زاوية حادة وصل بين طرفي الضلعين.

١٠) مثلث فيه زاوية منفرجة، وضلعان متطابقان.

ارسم زاوية منفرجة ضلعيها متساويين. صل بين طرفي الضلعين، المثلث منفرج الزاوية متساوي الضلعين.