حلول الأسئلة
السؤال
تمثل مواقع كل من الرياض وجدة وأيها رؤوس مثلث كما في الشكل أدناه . غذا كان محيط هذا المثلث 2198 km , فأوجد المسافة الجوية بين كل من المدن الثلاث .
الحل
الحل :
محيط المثلث = مجموع أطوال أضلاعه
المسافة بين الرياض وجدة =
المسافة بين الرياض وأبها =
المسافة بين جدة وأبها =
مشاركة الحل
التهيئة للفصل الأول
أجب عن الاختبار الآتي انظر المراجعة السريعة قبل الإجابة عن الاختبار.
.JPG)
أوجد قيم x,y في كل مما يأتي مقرباً إلى أقرب عشر:
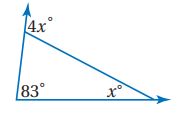
1)
الحل:
الزاوية الخارجية عن المثلث = مجموع الزاويتين الداخليتين البعيدتين.
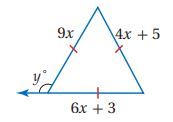
2)
الحل:
بما أن المثلث جميع أضلاعه متطابقة إذاً:
بما أن المثلث جميع أضلاعه متطابقة إذاً: جميع زواياه متطابقة و = .
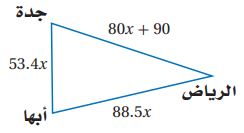
3) مدن: تمثل مواقع كل من الرياض وجدة وأبها رؤوس مثلث كما في الشكل أدناه إذا كان محيط هذا المثلث 2198km فأوجد المسافة الجوية بين كل من المدن الثلاث.
الحل:
محيط المثلث = مجموع أطوال أضلاعه.
- المسافة بين الرياض وجدة = .
- المسافة بين الرياض وأبها = .
- المسافة بين جدة وأبها = .
حدد ما إذا كان متوازيين أو متعامدين أو غير ذلك في كل مما يأتي:
.A(3,3),B(8,2),C(6, -1),D(1,0) (4
:الحل
.بما أن ميل كل متساويين إذاً فهما متوازيين
.A(4,2),B(1,-3),C(-3,5),D(2,2) (5
:الحل
.بما أن ميل كل من حاصل ضربهم = -1 إذاً فهما متعامدان
.A(-8,-7),B(4,-4),C(-2,-5),D(1,7) (6
:الحل
.بما أن ميل كل من غير متساويين فهما غير متوازيين وليس حاصل ضربهم =-1 إذا فهمت غير ذلك
7) حدائق: صمم مهندس رسماً لحديقة رباعية الشكل إحداثيات رؤوسها: A(-2,1),B(3,-3),C(5,7),D(-3 ,4) إذا رسم ممرين يقطعانها , فهل الممران متعامدان؟ فسر اجابتك.
الحل:
بما أن ميل كل من حاصل ضربهم = -1 إذاً فهما متعامدان.
أوجد المسافة بين كل نقطتين ثم أوجد احداثيات نقطة منتصف القطعة الواصلة بينهما في كل مما يأتي:
.J(-6,2),K(-1,3) (8
:الحل
.R(2,5),S(8,4) (9
:الحل
10) مسافات: وقف شخص على النقطة (20,80)T من مستوى احداثي ورغب في الانتقال الى كل من (60,20)U و(85,110)V فما أقصر مسافة يمكن أن يقطعها الشخص؟ فسر اجابتك.
الحل:
أقصر مسافة يقطعها الشخص هي من النقطة T إلى U >.