حل أسئلة تدرب وحل المسائل
صنف كلاً من أزواج الزوايا الآتية إلى: متتامتين، أو متكاملتين، أو غير ذلك:
٨- 
متتامتان، فمجموع قياسات الزاويتان = ٤٠ + ٥٠ = ٩٠°
٩- 
متكاملتان، فمجموع قياسات الزاويتان = ١٣٠ + ٥٠ = ١٨٠°
١٠- 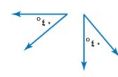
غير ذلك، فمجموع قياسات الزاويتان = ٤٠ + ٤٠ = ٨٠°
١١- .JPG)
متتامتان، فمجموع قياسات الزاويتان = ٣٠ + ٦٠ = ٩٠°
١٢- .JPG)
متتامتان، فمجموع قياسات الزاويتان = ٧٥ + ١٥ = ٩٠°
١٣- 
متكاملتان، فمجموع قياسات الزاويتان = ١٨٠° = ٩٥ + ٨٥
أوجد قيمة س في كل من الأشكال الآتية:
١٤- 
س= ١٢٨° الزاويتان متقابلتان بالرأس.
١٥- .JPG)
س = ٨٨° الزاويتان متقابلتان بالرأس.
١٦- 
الزاويتان متكاملتان، س = ١٨٠ - ١٤٠ = ٤٠°
١٧- 
الزاويتان متكاملتان، س = ١٨٠ - ٢٥ = ١٥٥°
١٨- 
الزاويتان متتامتان، س = ٩٠ - ٢٥ = ٦٥°
١٩- 
الزاويتان متتامتان، س = ٩٠ - ٥٥ = ٣٥°
٢٠- خيول: ما قيمة س في الحاجز المبين في الصورة المجاورة؟
س = ٩٠°
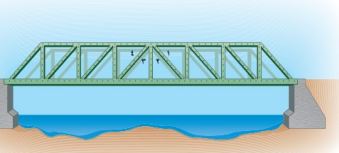
٢١- جسور: يتكون جسر من عدة دعائم مستقيمة كما في الشكل أدناه اكتب مسألة يمكن حلها بالرجوع إلى الزوايا المشار إليها بالأرقام ١ - ٤ في الشكل.
إذا كان قياس الزاوية ١ = ٥٠° فأوجد قياس الزاوية ٢.
٢٢- إذا كانت الزاويتان أ، ب متتامتين، ق أ = ٤٠° فأوجد ق ب.
أ، ب متتامتان، إذن مجموع قياسي الزاويتين = ٩٠°
إذن ب = ٩٠ - ٤٠ = ٥٠°
٢٣- إذا كانت الزاويتان جـ، د متكاملتان ق د = ٦٥°، فأوجد ق جـ.
جـ، د، متكاملتان، إذن مجموع قياسي الزاويتان = ١٨٠°
إذن ج μ = ١٨٠ - ٦٥ = ١١٥°
كهرباء: استعمل الصورة المجاورة التي تمثل أحد أبراج كهرباء الضغط العالي المنتشرة في المملكة للإجابة عن الأسئلة ٢٤ - ٢٨:
صنف أزواج الزوايا الآتية:
٢٤- ١ ٢
بما أن مجموع قياسهما يساوي ١٨٠°، إذن الزاويتان متكاملتان.
٢٥- ٢ ٤
متقابلتان بالرأس
٢٦- ٣ ٤
بما أن مجموع قياسهما يساوي ١٨٠°
٢٧- ١ ٣
متقابلتان بالرأس.
٢٨- إذا كان ق ٣ = ٤٦°، فأوجد ق ٢، ق١
μ ٢ = ١٨٠ - ٤٦ = ١٣٤°
μ ١ = μ ٣ = ٤٦°
حدد إذا كانت كل عبارة من العبارات الآتية صحيحة أحياناً، أو صحيحة دائماً، أم غير صحيحة، ثم فسر إجابتك.
٢٩- الزاويتان المتقابلتان بالرأس متطابقتان.
صحيحة دائماً، الزاويتان المتقابلتان بالرأس متطابقتان.
٣٠- الزاويتان المتقابلتان بالرأس لهما القياس نفسه.
صحيحة دائماً، الزاويتان المتقابلتان بالرأس متطابقتان.
٣١- الزاويتان القائمتان متتامتان.
غير صحيحة، قياس كل زاوية قائمة = ٩٠°
٣٢- الزاويتان المنفرجتان متكاملتان.
غير صحيحة، بما أن قياس الزاوية المنفرجة أكبر من ٩٠° فإن مجموع قياسي زاويتين منفرجتين سيكون أكبر من ١٨٠°
٣٣- الزاويتان المتقابلتان بالرأس متتامتان.
صحيحة أحياناً، إذا كان قياس كل من الزاويتين المتقابلتين بالرأس ٤٥° فإنهما متتامتين.
٣٤- تبرير: أجب عن كل من الأسئلة الآتية:
أ. ما نوع الزاوية المكملة لزاوية حادة؟
زاوية منفرجة، لأن الزاوية الحادة يكون قياسها أقل من ٩٠° لذا فهي تحتاج إلى زاوية قياسها أكبر من ٩٠° لتكملها.
ب. ما نوع الزاوية المكملة لزاوية قائمة؟
زاوية قائمة، لأن قياس الزاوية القائمة = ٩٠° لذا فهي تحتاج إلى زاوية قائمة لتكملها.
جـ. هل يمكن لزاويتين حادتين أن تكونا متكاملتين؟ برر إجابتك.
لا، فمجموع قياس زاويتين حادتين لا يمكن أن يصل ل ١٨٠ ° لأن قياس كل زاوية حادة أقل من ٩٠°
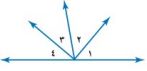
٣٥- تحد: انظر إلى الشكل المجاور إذا كان ق ١ = ق ٢، وكان ق ٣ = ق ٤، فماذا يمكن أن نستنتج عن مجموع قياسي ١ ، ٣؟ برر إجابتك.
ق ١ = ق ٢
ق ٣ = ق ٤
ق ١ + ق ٢ + ق ٣ + ق ٤ = ١٨٠°
E ق ١ + ق 1 + ق ٣ + ق ٣ = ١٨٠°
E ٢ ( ق ١ + ق ٣) = ١٨٠°
E ق ١ + ق ٣ = ٩٠°
٣٦- اكتب إذا وجدت زاويتين لهما الزاوية المكملة نفسها فما الوصف الصحيح لقياس هاتين الزاويتين؟ فسر إجابتك.
يجب أن يكون للزاويتين القياس نفسه فإذا كان لكل من الزاويتين الزاوية المكملة نفسها ولتكن س° فإن قياس كل من الزاويتين يساوي (١٨٠ - س) °
أي أن لهما القياس نفسه.
٣٧- إذا كانت الزاويتان س، ص متتامتان، وكان قياس س يساوي ٦٠، فما قياس ص؟
أ. ٣٠°
ب. ٦٠°
جـ. ٩٠°
د. ١٢٠°

.JPG)
.JPG)


.JPG)