أوجد قيمة س في كل من المثلثين الآتيين:

س + ٧٥ + ٦٠ = ١٨٠°

س = ١٨٠ - ١٣٥ = ٤٥°

حل أسئلة تأكد

صنف كلاً من المثلثين الآتيين إلى حاد الزوايا أو قائم الزاوية أو منفرج الزاوية:

١-

الزاوية التي قياسها ١١٥° هي زاوية منفرجة، إذن هذا المثلث منفرج الزاوية.

٢-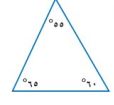

جميع الزوايا هي حادة، إذن هذا المثلث حاد الزوايا.

أوجد قيمة س في كل من المثلثين الآتيين:

٣-

س + ٧٥ + ٦٠ = ١٨٠°

س = ١٨٠ - ١٣٥ = ٤٥°

٤-

س + ٣٥ + ٤٥ = ١٨٠°

س = ١٨٠ - ٧٥ = ١٠٥°

٥- قوارب: ما قيمة س المبينة في القارب المجاور؟

س + ٢٠ + ٧٠ = ١٨٠°

س = ١٨٠ - ٩٠ = ٩٠°

صنف كلاً من المثلثين الآتيين إلى: مختلف الأضلاع أو متطابق الضلعين أو متطابق الأضلاع:

٦-

الأضلاع الثلاثة متطابقة، إذن فهو مثلث متطابق الأضلاع ومتطابق الضلعين.

٧-

لا يوجد أضلاع متطابقة، إذن فهو مثلث مختلف الأضلاع.