صنف كلاً من المثلثات الآتية المرسومة أو التي أعطيت قياسات زواياها إلى: حاد الزوايا، أو قائم الزاوية، أو منفرج الزاوية:

٩٠° - ٧٥° - ١٥°

الزاوية التي قياسها ٩٠° هي زاوية قائمة، إذن هذا المثلث قائم الزاوية.

حل أسئلة تدرب وحل المسائل

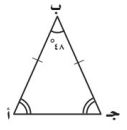
صنف كلاً من المثلثات الآتية المرسومة أو التي أعطيت قياسات زواياها إلى: حاد الزوايا، أو قائم الزاوية، أو منفرج الزاوية:

٨-

الزاوية التي قياسها ٩٠° هي زاوية قائمة، إذن هذا المثلث قائم الزاوية.

٩-

جميع الزوايا حادة إذن المثلث حاد الزوايا.

١٠-

جميع الزوايا هي زاوية حادة، إذن هذا المثلث حاد الزوايا.

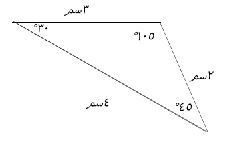
١١- ١٠٠° - ٤٥° - ٣٥°

الزاوية التي قياسها ١٠٠° هي زاوية منفرجة، إذن هذا المثلث منفرج الزاوية.

١٢- ٩٠° - ٧٥° - ١٥°

الزاوية التي قياسها ٩٠° هي زاوية قائمة، إذن هذا المثلث قائم الزاوية.

١٣- ١١٤° - ٢٣° - ٣٣°

الزاوية التي قياسها ١١٤° هي زاوية منفرجة، إذن هذا المثلث منفرج الزاوية.

أوجد قيمة س في كل من المثلثات الآتية:

١٤-

س= ١٨٠ - ١٥٠ = ٣٠°

١٥-

س= ١٨٠ - ٨٠ = ١٠٠°

١٦-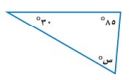

س= ١٨٠ - ١١٥ = ٦٥°

١٧- ٧٠° - ٦٠° - س°

س = ١٨٠ - ٨٥ = ٩٥°

١٨- س° - ٦٠° - ٢٥°

س= ١٨٠ - ٦٠ = ١٢٠°

١٩- س° - ٣٥° - ٢٥°

س= ١٨٠ - ٦٠ = ١٢٠°

٢٠- بنايات: ما قيمة س في الشكل أدناه؟

٢٥ + ٩٠ + س = ١٨٠°

س = ١٨٠ - ١١٥ = ٦٥°

٢١- متنزهات: الشكل أدناه يبين خيمة على شكل مثلث في أحد المتنزهات ما قيمة س؟

س + ٥٠ + ٦٥ = ١٨٠°

س = ١٨٠ - ١١٥ = ٦٥°

صنف كلاً من المثلثات الموضحة في الأسئلة ٢٢ - ٢٦ إلى مختلف الأضلاع، أو متطابق الضلعين، أو متطابق الأضلاع:

٢٢-

يوجد ضلعين متطابقين، إذن المثلث هو متطابق الضلعين.

٢٣-

الأضلاع الثلاثة متطابقة، إذن فهو مثلث متطابق الأضلاع ومتطابق الضلعين.

٢٤-

المثلث متطابق الضلعين.

٢٥- أطوال أضلاعه: ٩سم - ١١سم - ١٣سم

مثلث مختلف الأضلاع.

٢٦- أطوال أضلاعه: ٥سم - ٦سم - ٥سم

مثلث متطابق الضلعين.

٢٧- ما قياس الزاوية الثالثة في مثلث قياس الزاويتين الأخريين فيه: ٢٥° و٥٠°؟

قياس الزاوية الثالثة = ١٨٠ - (٢٥ + ٥٠) = ١٠٥°

٢٨- ما قياس الزاوية الثالثة في مثلث قائم الزاوية قياس إحدى زواياه ٣١°؟

قياس الزاوية الثالثة = ١٨٠ - (٩٠ + ٣١) = ٥٩°

٢٩- ما العلاقة بين الزاويتين الحادتين في المثلث القائم الزاوية؟

العلاقة بين الزاويتين الحادتين في المثلث القائم: متتامتان أي مجموعهما يساوي ٩٠°

٣٠- مسألة مفتوحة: ارسم مثلثاً مختلف الأضلاع ومنفرج الزاوية مستعملاً المنقلة والمسطرة ثم سجل عليه أطوال أضلاعه وقياسات زواياه.

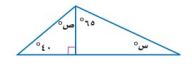
٣١- تحد: أوجد قيمة كل من س، ص في الشكل أدناه:

س + ٩٠ + ٦٥ = ١٨٠°

س = ١٨٠ - ١٥٥ = ٢٥°

ص = ٩٠ + ٤٠ = ١٤٠°

ص = ١٨٠ - ١٣٠ = ٥٠°

٣٢- اكتب: لماذا توجد زاويتان حادتان على الأقل في أي مثلث؟ وضح إجابتك بالرسم.

يجب أن تتقاسم زوايا المثلث الثلاثة المقدار ١٨٠°

فإذا كان قياس إحدى الزوايا ٨٩° أو أقل فإن ٩١° الباقية تتوزع على الزاويتين الأخريين. مما يجعل إحداهما على الأقل زاوية حادة.

وإذا كان قياس إحدى الزوايا ٩٠° أو أكثر فإن ٩٠° الباقية تتوزع على الزاويتين الأخريين مما يجعل كلا منهما زاوية حادة.

٣٣- إذا كان قياس زاويتين في مثلث هو ٢٥° - ٦٠° فما قياس الزاوية الثالثة؟

أ. ١٥°

ب. ٨٥°

جـ. ٩٥°

د. ١١٥°

٣٤- إجابة قصير: أ ب جـ مثلث متطابق الضلعين فيه ق $\angle$ب = ٤٨° ، ق$\angle$أ = ق $\angle$جـ، فما ق$\angle$أ؟

ق (أ) + ق(جـ) = ١٨٠ - ٤٨ = ١٣٢

ق (‌أ) = ١٣٢ ÷ ٢ = ٦٦