اشرح طريقتين مختلفتين على الأقل لإيجاد مساحة السداسي المنتظم مضمناً إجابتك رسماً توضيحياً لذلك.

• الطريقة الأولى: قسم المضلع السداسي أفقياً إلى شبهي منحرف ثم أوجد مجموع مساحتها.
• الطريقة الثانية: قسم المضلع سداسي رأسياً إلى مثلثين ومستطيل وأوجد مساحة كل شكل منها ثم أوجد مجموع هذه المساحات؟

حل أسئلة تدرب وحل المسائل

أوجد مساحة الأشكال المركبة الآتية مقرباً الجواب إلى أقرب جزء من عشرة إذا لزم ذلك:

٥-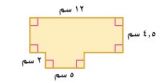

م١ = الطول × العرض = ٤,٥ × ١٢ = ٥٤ سم^٢

م٢ = الطول × العرض = ٥ × ٢ = ١٠ سم^٢

م الكلية = ٥٤ + ١٠ = ٦٤ سم^٢

٦ -

م١ = الطول × العرض = ٢٤ × ٨ = ١٩٢

م ٢ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ق ع = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ١٢ × ٨ = ٤٨

م الكلية = ٤٨ + ١٩٢ = ٢٤٠ ملم^٢

٧-

م ١ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ق ع = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ١٦ × ١٥ = ١٢٠

م٢ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ط نق^٢ = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٣,١٤ × ٦٤ = ١٠٠ تقريباً.

م الكلية = ١٠٠ + ١٢٠ = ٢٢٠ سم^٢

٨-

م ١ = طول الضلع × نفسه = ٧ × ٧ = ٤٩

م ٢ = مساحة نصفي الدائرة = ط نق^٢ = ٣,١٤ × (٣،٥)^٢ = ٣٨,٤

م الكلية = ٤٩ + ٣٨,٤ = ٨٧,٤ م^٢

٩-

م ١ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ع (ق١ + ق ٢) = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٣,٦ × (٧ + ٩) = ٢٨,٨

ارتفاع المثلث = ٦,٤ - ٣,٦ = ٢,٨

إذن م٢ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ق ع = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٧ ٢,٨ = ٩,٨

م الكلية = ٢٨,٨ + ٩,٨ = ٣٨,٦ قدم مربع.

١٠-

م١ = الطول × العرض = ٦ × ٢٠ = ١٢٠

م ٢ = $\frac{\mathrm{١}}{\mathrm{٢}}$ ع (ق١ + ق٢) = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٤ × (٢٠ + ١٠) = ٦٠

م الكلية = ١٢٠ + ٦٠ = ١٨٠ سم^٢

١١- نجارة: صمم أحمد طاولة كما في الشكل أدناه ما مساحة سطحها؟

تقسم إلى ٣ أشكال: مستطيل ٢ شبه منحرف.

مساحة المستطيل = ٥ × ١٢ = ٦٠

مساحة شبه المنحرف = $\frac{\mathrm{١}}{\mathrm{٢}}$ ع (ق١ + ق٢)

= $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٣,٥ × (٥+١٢) = ٢٩,٧٥

مساحة ٢ شبه منحرف = ٥٩,٥

إذن المساحة الكلية = ٥٩,٥ + ٦٠ = ١١٩,٥ قدم مربع.

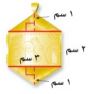
١٢- مجوهرات: يبين الشكل الآتي حلية ذهبية ما مساحتها؟

مساحة المستطيل = ٢ × ٣ = ٦

بما أن المثلثات متساويان مساحتهما واحدة.

= ٢($\frac{\mathrm{١}}{\mathrm{٢}}$ ق ع) = ق ع = ٣ × ١ = ٣

المساحة الكلية = ٦ × ٣ = ٩ سم^٢

أوجد مساحة المنطقة المظللة مقرباً الجواب إلى أقرب جزء من عشرة:

١ ٣-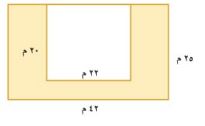

مساحة الشكل كله = الطول × العرض = ٢٥ × ٤٢ = ١٠٥٠

مساحة المنطقة غير المظللة = الطول × العرض = ٢٢ × ٢٠ = ٤٤٠

إذن مساحة المنطقة المظللة = ١٠٥٠ - ٤٤٠ = ٦١٠ م^٢

١ ٤-

مساحة الشكل كله = $\frac{\mathrm{١}}{\mathrm{٢}}$ ع ق = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ١٥ × ١٠ = ٧٥

مساحة المثلث الصغير = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٩ × ٦ = ٢٧

إذن مساحة المنطقة المظللة = ٧٥ - ٢٧ = ٤٨ سم^٢

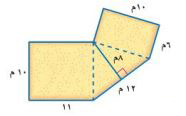
١٥- سجاد: ترغب والدة ليان في تغطية أرضية صالة منزلها بالسجاد كما في الشكل المجاور ما مساحة السجاد المطلوب شراؤه؟

مساحة المثلث = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ١٢ × ٨ = ٤٨

مساحة المستطيل الصغير = ٦ × ١٠ = ٦٠

مساحة المستطيل الكبير = ١١ × ١٠ = ١١٠

إذن مساحة الشكل = ١١٠ + ٦٠ + ٤٨ = ٢١٨ م^٢

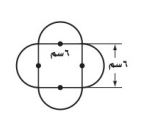
١٦- تحد: يمثل الشكل المجاور بركة محاطة بممر من الورد عرضه متران ما مساحة الممر؟

المساحة الخارجية = ١١٣,١ سم^٢

المساحة الداخلية = ٥٠,٣ سم^٢

مساحة الممر = ١١٣,١ - ٥٠,٣ = ٦٢,٨ سم^٢

١٧- اكتب: اشرح طريقتين مختلفتين على الأقل لإيجاد مساحة السداسي المنتظم مضمناً إجابتك رسماً توضيحياً لذلك.

• الطريقة الأولى: قسم المضلع السداسي أفقياً إلى شبهي منحرف ثم أوجد مجموع مساحتها.
• الطريقة الثانية: قسم المضلع سداسي رأسياً إلى مثلثين ومستطيل وأوجد مساحة كل شكل منها ثم أوجد مجموع هذه المساحات؟

١٩- ما المساحة الكلية للشكل أدناه؟

أ. ٩٢,٩ سم^٢

ب. ٥٦,٥ سم

جـ. ٦٤,٣ سم^٢

د. ٣٦,٠ سم

مساحة نصف الدائرة = $\frac{\mathrm{١}}{\mathrm{٢}}$ ط نق^٢

مساحة نصف الدائرة = $\frac{\mathrm{١}}{\mathrm{٢}}$ ط (٣)^٢ ≈ ١٤,١٤

بما أنه يوجد ٤ أنصاف للدائرة إذن

مساحة أنصاف الدائرة = ٤ × ١٤,١٤ ≈ ٥٦,٥٦

مساحة المربع = طول الضلع × نفسه.

مساحة المربع = (٦)^٢ = ٣٦

مساحة الشكل = ٥٦,٥٦ + ٣٦ ≈ ٩٢,٥٦

١٩- يبين الشكل أدناه مزرعة خضراوات مستطيلة الشكل طولها ١٨١ م وعرضها ٤٨م زرع منها جزء مستطيل الشكل طوله ٣٢م وعرضه ٢١م بالفواكه ما مساحة الجزء المزروع بالخضراوات؟

أ. ٨٦٨٨ م^٢

ب. ٨٠١٦ م^٢

جـ. ٨٦٣٥ م^٢

د. ٢٨٢ م^٢

مساحة المستطيل (المزرعة كلها) = الطول × العرض.

= ١٨١ × ٤٨ = ٨٦٨٨

مساحة المستطيل (الجزء المزروع) = الطول × العرض.

= ٣٢ × ٢١ = ٦٧٢

مساحة المنطقة المزروعة = ٨٦٨٨ - ٦٧٢ = ٨٠١٦ م^٢

٢٠- مهارة سابقة: لوحظ تناقص أسعار الآلات الحاسبة ففي عام ١٤٢٥م كان سعر آلة حاسبة من نوع ما ١٢٥ ريال أصبح ١٠٧ ريالات عام ١٤٣٠ هـ، ثم ٨٩ ريالاً عام ١٤٣٥هـ إذا استمر تناقص سعر الآلة الحاسبة بالمعدل نفسه فاستعمل استراتيجية البحث عن نمط في إيجاد سعر آلة حاسبة من النوع نفسه عام ١٤٤٥ هـ.

١٢٥- ١٠٧ = ١٨

١٠٧ - ١٨ = ٨٩

نستنتج من ذلك أن كل ٥ سنوات يقل سعر الآلة الحاسبة بمقدار ١٨ ريال إذن في عام ١٤٤٠ هـ يكون الآلة الحاسبة = ٨٩ - ١٨ = ٧١ ريال.