توسع: المخططات والمساحة السطحية
أ) اصنع مخططين لصندوقين على شكل متوازي مستطيلات.
حلل النتائج:
١ - يتكون المخطط الوارد في النشاط السابق من مستطيلات ما عدد هذه المستطيلات؟
يتكون من ٦ مستطيلات.
٢ - وضح كيف يمكنك إيجاد المساحة الكلية لهذه المستطيلات؟
من الشكل أن كل مستطيلات متساويان نوجد مساحة كل مستطيل ونضرب × ٢ ثم نجمع.
ارسم مخططاً لكل شكل فيما يأتي واحسب مساحة هذا المخطط.
٣ - .JPG)
مساحة المخطط = ١٢٠ م٢
٤ - .JPG)
مساحة المخطط = ٤٨ دسم٢
٥ - 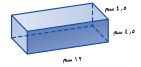
مساحة المخطط = ٢٤٣ سم٢
٦ - مساحة متوازي المستطيلات هي المساحة الكلية للمخطط اكتب معادلة تبين كيف يمكن حساب مساحة سطح متوازي المستطيلات أدناه باستعمال الطول ((ل)) والعرض ((ض)) والارتفاع ((ع))
مساحة المخطط = الطول × العرض × الارتفاع.
= ل × ض × ع
٧ - احسب مساحات أسطح المكعبات التي أطوال أحرفها وحدة واحدة ووحدتان و٣ وحدات ومثل الأزواج المرتبة (طول الحرف، مساحة السطح).
| طول الحرف | مساحة السطح | الزوج المرتب |
| ١ | ١ | (١، ١) |
| ٢ | ٨ | (٢، ٨) |
| ٣ | ٢٧ | (٣، ٢٧) |
٨ - خمن: صف ما يحدث لمساحة سطح مكعب إذا تم مضاعفة أبعاده مرتين وإذا تم مضاعفتها ثلاث مرات.
يزداد مساحة السطح ٣ أمثال الحرف.
ارسم مخططاً لكل شكل فيما يأتي:
٩ - .JPG)
١٠ - 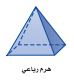
١١ - وضح كيف يختلف مخطط الهرم الثلاثي عن مخطط الهرم الرباعي.
يختلف في شكل القاعدة وعدد الأوجه الجانبية، فالقاعدة في الهرم الثلاثي على شكل مثلث، أما في الهرم الرباعي فتكون مربعة، وعدد الأوجه في الهرم الثلاثي تكون ٤ أوجه أما في الهرم الرباعي تكون ٥ أوجه.
١٢ - صف كيف يمكنك حساب مساحة سطح الهرم الثلاثي.
بحساب مساحة كل سطح من الأوجه وجمع مساحاتها.
= ٤ × (٠,٥ × طول القاعدة × الارتفاع)
١٣ - صف كيف يمكنك حساب مساحة سطح الهرم الرباعي
بحساب مساحة كل سطح من الأوجه وجمع مساحاتها
= (طول ضلع المربع × نفسه) + ٣ × (٠,٥ × طول القاعدة × الارتفاع)
١٤ - احسب مساحة سطح هرم قاعدته مربع طول ضلعه ٨سم، وارتفاع كل مثلث على جانبه ٥سم.
مساحة سطح الهرم = (٨ × ٨) + ٤ × (٠,٥ × ٨ × ٥) = ١٤ سم٢

.JPG)



.JPG)
.JPG)
.JPG)