حل أسئلة التهيئة
استعمل جدول القيم لتمثيل كل دالة فيما يأتي بيانياً:
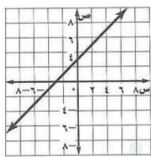
١) ص = س + ٣
| س | ص = س + ٣ | ص |
| -١ | ص = -١ + ٣ | ٢ |
| ٠ | ص = ٠ + ٣ | ٣ |
| ١ | ص = ١ + ٣ | ٤ |
| ٢ | ص = ٢ + ٣ | ٥ |
| ٣ | ص = ٣ + ٣ | ٦ |
٢) ص = ٢س + ٢
| س | ص = ٢س + ٢ | ص |
| -١ | ص = -٢ + ٢ | ٠ |
| ٠ | ص = ٠ + ٢ | ٢ |
| ١ | ص = ٢ + ٢ | ٤ |
| ٢ | ص = ٤ + ٢ | ٦ |
| ٣ | ص = ٦ + ٢ | ٨ |
٣) ص = -٢س - ٣
| س | ص = -٢س - ٣ | ص |
| -١ | ص = -١× -٢ - ٣ | -١ |
| ٠ | ص = ٠ - ٣ | -٣ |
| ١ | ص = -٢ -٣ | -٥ |
| ٢ | ص = -٤ - ٣ | -٧ |
٤) ص = ٠,٥س - ١
| س | ص = ٠,٥س - ١ | ص |
| -١ | ص = -٥ -١ | -١,٥ |
| ٠ | ص = ٠ - ١ | -١ |
| ١ | ص = -٠,٥ -١ | -٠,٥ |
| ٢ | ص = -٠,٥ × ٢ -١ | ٠ |
٥) ٤س - ٣ص = ١٢
| س | ص |
| -١ | -٥,٣ |
| ٠ | -٤ |
| ١ | -٢,٧ |
| ٢ | ١,٣ |
٦) ٣ص = ٦ + ٩س
بقسمة الطرفين على ٣
ص = ٢ + ٣س
| س | ص |
| -١ | -١ |
| ٠ | ٢ |
| ١ | ٥ |
| ٢ | ٨ |
٧) ص - س = ١
بإضافة س إلى الطرفين
ص = س + ١
| س | ص |
| -١ | ٠ |
| ٠ | ١ |
| ١ | ٢ |
| ٢ | ٣ |
٨) ٣ص = ٦س
بقسمة الطرفين على ٣
ص = ٢س
| س | ص |
| -١ | -٢ |
| ٠ | ٠ |
| ١ | ٢ |
| ٢ | ٤ |
٩) توفير: مع محسن ١٠٠ ريال، ويخطط لتوفير ١٠ ريالات أسبوعاً، مثل بيانياً معادلة تبين المبلغ الكلي (م) الذي سيوفره محسن في (س) أسبوعاً.
حدد إذا كانت كل ثلاثية حدود فيما يأتي تشكل مربعاً كاملاً، اكتب "نعم" أو "لا" وإذا كانت كذلك فحللها:
١٠) أ٢ + ١٢أ + ٣٦
نعم، (أ + ٦)٢
الحد الأول مربع كامل وكذلك الحد الثالث وبما أن ٢ × جذر الحد الأول × جذر الحد الثالث = ١٢ إذن الحد الأوسط مربع كامل أيضاً إذن ثلاثية الحدود تشكل مربعاً كاملاً.
١١) س٢ + ٥س + ٢٥
لا.
١٢) س٢ - ١٢س + ٣٢
لا.
١٣) س٢ + ٢٠س + ١٠٠
نعم، (٢س + ١٠)٢
الحد الأول مربع كامل وكذلك الحد الثالث وبما أن ٢× جذر الحد الأول × جذر الحد الثالث = ٢٠ إذن الحد الأوسط مربع كامل أيضاً إذن ثلاثية الحدود تشكل مربعاً كاملاً.
١٤) ٤س٢ + ٢٨س + ٤٩
نعم، (٢س + ٧)٢
الحد الأول مربع كامل وكذلك الحد الثالث وبما أن ٢× جذر الحد الأول × جذر الحد الثالث = ٢٨ إذن الحد الأوسط مربع كامل أيضاً إذن ثلاثية الحدود تشكل مربعاً كاملاً.
١٥) ك٢ - ١٦ك + ٦٤
نعم، (ك - ٨)٢
الحد الأول مربع كامل وكذلك الحد الثالث وبما أن ٢× جذر الحد الأول × جذر الحد الثالث = ١٦ إذن الحد الأوسط مربع كامل أيضاً إذن ثلاثية الحدود تشكل مربعاً كاملاً.
١٦) أ٢ - ٢٢أ + ١٢١
نعم، (أ - ١١)٢
الحد الأول مربع كامل وكذلك الحد الثالث وبما أن ٢× جذر الحد الأول × جذر الحد الثالث = ٢٢ إذن الحد الأوسط مربع كامل أيضاً إذن ثلاثية الحدود تشكل مربعاً كاملاً.
١٧) ٥ت٢ - ١٢ت + ٢٥
لا.
١٨) س٢ + ٢س + ١
نعم، (س - ٣)٢

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)