حلل كلاً مما يأتي إلى عوامله الأولية: مثال ٣

٢٠

٢٠: ٢×٢×٥

حل أسئلة تأكد

١) هل جميع الأعداد الزوجية أعداد غير أولية؟ ادعم إجابتك بالرسم.

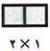
لا، العدد ٢ عدد زوجي لكنه أولي لأن له قاسمان فقط هما ١ و ٢

ويمكن توضيحهما بترتيبين مختلفين تماماً.

٢) هل جميع الأعداد الفردية أعداد أولية؟ ادعم أجابتك بالرسم.

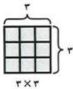
لا، ليست جميع الأعداد الفردية أعداد أولية، فمثلاً العدد ٩ هو عدد فردي وغير أولي، ويمكن توضيحه بثلاث طرائق مختلفة.

استعمل النماذج لتحدد ما إذا كان كل عدد مما يأتي أولياً أو غير أولي، واصفاً الطرائق المختلفة التي استعملتها في ترتيبها:

٣) ١٣

العدد ١٣ عدد أولي: ١×١٣، ١٣×١

٤) ١٠

العدد ١٠ غير أولي: ١×١٠، ١٠×١، ٢×٥، ٥×٢

٥) ١١

العدد ١١ عدد أولي: ١×١١، ١١×١

٦) ٨

العدد ٨ غير أولي: ١×٨، ٨×١، ٢×٤، ٤×٢

٧) ١٧

العدد ١٧ أولي: ١×١٧، ١٧×١

٨) ٩

العدد ٩ غير أولي: ١×٩، ٩×١، ٣×٣

٩) صنعت أروى ١٢ فطيرة للعشاء، ووضعتها على طبق في ٣ صفوف، في كل منها ٤ فطائر بكم طريقة أخرى يمكنها ترتيب الفطائر في صفوف متساوية؟

عدد الطرق يساوي ٥ ويمكن ترتيبها كالآتي:

١×١٢، ٢×٦، ٤×٣، ١٢×١، ٦×٢

صف واحد به ١٢ فطيرة أو ١٢ صف بكل منهم فطيرة واحدة أو صفين بكل منهما ٦ فطائر أو ٦ صفوف بكل منهم فطيرتين أو ٤ صفوف بكل منهم ٣ فطائر.

١٠) اختر عدداً بين ٢٠، ٣٠، ثم استعمل النماذج لتبين ما إذا كان العدد أولي أو غير أولي.

٢١ هو عدد غير أولي لأنه يمكن توضيحه بأربعة ترتيبات مختلفة.

١١) هل هناك علاقة بين عدد الترتيبات المستطيلة الممكنة عند عمل نماذج لعدد ما وعدد قواسمه؟ برر إجابتك.

نعم، عدد الترتيبات المستطيلة = عدد نماذج قواسم العدد.

حدد ما إذا كان العدد الممثل في كل شكل مما يأتي أولياً أو غير أولي: مثال ١

١)

أولي لأنه يمثل بطريقتين فقط إما ١×٥ أو ٥×١

٢)

غير أولي لأن له أكثر من قاسمان: ٢×٣، ٣×٢، ١×٦، ٦×١

حدد ما إذا كان كل عدد مما يأتي أولياً أو غير أولي، وادعم إجابتك بالنتائج: المثالان ٢،١

٣) ٩

العدد ٩ غير أولي: ١×٩، ٩×١، ٣×٣

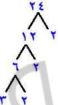
٤) ٢٤

العدد ٢٤ غير أولي: ١×٢٤، ٢×١٢، ٣×٨

٥) ١٧

العدد ١٧ أولي: ١×١٧، ١٧×١

٦) ٣١

العدد ٣١ أولي: ١×٣١، ٣١×١

حلل كلاً مما يأتي إلى عوامله الأولية: مثال ٣

٧) ١٨

١٨: ٢×٣×٣

٨) ٢٠

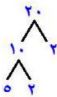
٢٠: ٢×٢×٥

٩) ٢٤

٢٤: ٢×٢×٢×٣

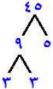
١٠) ٤٥

٤٥: ٥×٣×٣

١١) هل يستطيع خلف أن يرتب ٢١ لعبة في صفوف بالتساوي بأكثر من طريقة؟ فسر إجابتك.

نعم يستطيع عن طريق: أن يجعل ٣ صفوف من ٧ سيارات أو ٧ صفوف من ٣ سيارات، صف واحد من ٢١ سيارة أو ٢١ صف من سيارة واحدة.

١٢) هل العدد ٣٣ أولي أم غير أولي؟ كيف عرفت ذلك؟

غير أولي لأنه يقبل القسمة على ١ وعلى نفسه وعلى ١١ وعلى ٣