اكتب مسألة يمكن حلها باستعمال نظرية فيثاغورس، ثم فسر كيف تحل المسألة.

قام بعض الطلاب بتزيين الفصل الدراسي وأرادوا أن يقسموا الحائط إلى جزأين، كل جزء على شكل مثلث، واستخدموا لتقسيم الحائط شريط من ورق الزينة.

إذا كان ارتفاع الحائط ٣ م، وطوله ٤م، فكم متراً يحتاج الطلاب لتقسيم الحائط؟

ج^٢ = ^٢ ٤ + ^٢ ٣

ج^٢ = ^٢ ٤ + ^٢ ٣

ج = $\sqrt{\mathrm{١٦} + \mathrm{٩}}=\sqrt{\mathrm{٢٥}}$ = ٥ م,

حل أسئلة تدرب وحل المسائل

اكتب معادلة يمكن استعمالها للإجابة عن كل سؤال مما يأتي ثم حلها وقرب الجواب إلى أقرب جزء من عشرة.

٥) كم ارتفاع الشجرة؟

ع^٢ = ^٢١٢ - ^٢٥

ع^٢ = ١٤٤ - ٢٥ = ١٦٩

ع = $\sqrt{\mathrm{١٦٩}}$ = ١٠,٩٠٨ ≈ ١١ م.

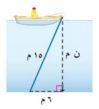
٦) ما عمق الماء؟

ن^٢ = ^٢١٥ - ^٢٦

ن^٢ = ٢٢٥ - ٣٦ = ١٨٩

ن = $\sqrt{\mathrm{١٨٩}}$ = ١٣,٧٤ ≈ ١٤م.

٧) كم يبعد الطائر عن الولد؟

س^٢ = ^٢٧٠ + ^٢٢٠

س^٢ = ٤٩٠٠ + ٤٠٠

س^٢ = ٥٣٠٠

س = $\sqrt{\mathrm{٥٣٠٠}}$ = ٧٢,٨ ≈ ٧٣ قدماً.

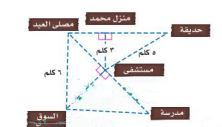
استعمل المخطط المجاور للإجابة عن الأسئلة ٨ - ١٠، وقرب الجواب إلى أقرب جزء من عشرة:

٨) كم يبعد منزل محمد عن الحديقة؟

بعد منزل محمد عن الحديقة = $\sqrt{\mathrm{٢٥} - \mathrm{٩}}=\sqrt{\mathrm{١٦}}$ = ٤كلم.

٩) صلى شخص في مصلى العيد، ثم قام بزيارة مريض في المستشفى، ثم ذهب إلى السوق، فما طول المسافة التي قطعها؟

• المسافة بين المصلى والمستشفى = $\sqrt{\mathrm{٣٦} - \mathrm{١٦}}=\sqrt{\mathrm{٢٠}}=\mathrm{٢}\sqrt{\mathrm{٥}}$
• المسافة التي قطعها = ٢$\sqrt{\mathrm{٥}}$ كلم.

١٠) كم تزيد المسافة بين الحديقة ومصلى العيد على المسافة بين السوق والمدرسة؟

• البعد بين منزل محمد والمصلى = $\sqrt{\mathrm{٢٠} - \mathrm{٩}}=\sqrt{\mathrm{١١}}$
• المسافة بين الحديقة والمصلى = ٣,٣ + ٤ = ٧,٣ كلم.
• المسافة بين المدرسة والسوق = $\sqrt{\mathrm{٦٤}.\mathrm{١٧} + \mathrm{١٦}}$ = ٥,٨ كلم.
• الفرق بين المسافتين = ٧,٣ - ٥,٨ = ١,٥ كلم.

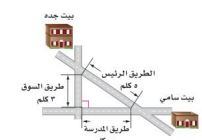
١١) مسافات: يرغب سامي في الذهاب من بيته إلى بيت جده، ما المسافة التي يوفرها إذا سلك الطريق الرئيس بدلاً من الطريقين الآخرين؟

^٢٥ = س^٢ + ^٢٣

س^٢ = ^٢٥ - ^٢٣

س = $\sqrt{\mathrm{٢٥} - \mathrm{٩}}=\sqrt{\mathrm{١٦}}$

س = ٤ كم.

المسافة التي يوفرها سامي = (٣ + ٤) - ٥

= ٧ - ٥ = ٢كم.

١٢) تسلية: يرغب أحمد في مشاهدة برامجه المحببة من خلال التلفاز ذي شاشة كبيرة؛ لذا رغب في شراء تلفاز جديد، وبعدا شاشته ٢٥ بوصة × ١٣,٦ بوصة، أوجد قطر شاشة التلفاز.

بعدا الشاشة هو طولا ساقي مثلث قائم الزاوية:

ج^٢ = ^٢٢٥ + ^٢١٣,٦

ج^٢ = ٦٢٥ + ١٨٤,٩٦

ج = $\sqrt{\mathrm{٩٦}, \mathrm{١٨٤}}$ = ٢٨,٤٥ بوصة.

١٣) هندسة: في الشكل المجاور، الرباعي أ ب جـ د فيه الزاوية د زاوية قائمة، والقطر أ جـ يعامد الضلع ب جـ، أوجد طول الضلع ب جـ؟

• طول $\overline{أ ج}=\sqrt{\mathrm{١٦} + \mathrm{٩}}=\sqrt{\mathrm{٢٥}}$ = ٥سم.
• طول _{ب ج}= $\sqrt{\mathrm{٢٥} + \mathrm{١٩}=\mathrm{٦٩}}=\sqrt{\mathrm{١٩٤}}$ = ١٣,٩ سم.

١٤) هندسة: أوجد طول الوتر أ ب، حيث طول القطعة أ د مطابق لطول د هـ، قرب الناتج إلى أقرب جزء من عشرة.

أ د = د هـ = ٤٠ وحدة

ب جـ د هـ مستطيل

إذاً د جـ ب هـ = ٢٥ وحدة.

ب جـ = ٤٠ وحدة.

أ جـ = ٤٠ - ٢٥ = ١٥ وحدة.

المثلث أ ب جـ = قائم الزاوية، طولا ساقيه ٤٠، ١٥ وحدة.

إذاً: (أب)^٢ = ^٢٤٠ = ^٢١٥

= ١٦٠٠ + ٢٢٥ = ١٨٢٥

أ ب = $\sqrt{\mathrm{١٨٢٥}}$

أ ب = ٤٢,٧ وحدة.

١٥) مسألة مفتوحة: اكتب مسألة يمكن حلها باستعمال نظرية فيثاغورس، ثم فسر كيف تحل المسألة.

قام بعض الطلاب بتزيين الفصل الدراسي وأرادوا أن يقسموا الحائط إلى جزأين، كل جزء على شكل مثلث، واستخدموا لتقسيم الحائط شريط من ورق الزينة.

إذا كان ارتفاع الحائط ٣ م، وطوله ٤م، فكم متراً يحتاج الطلاب لتقسيم الحائط؟

ج^٢ = ^٢٤ + ^٢٣

ج^٢ = ^٢٤ + ^٢٣

ج = $\sqrt{\mathrm{١٦} + \mathrm{٩}}=\sqrt{\mathrm{٢٥}}$ = ٥ م,

١٦) اكتشف المختلف: تمثل كل مجموعة من الأعداد الآتية أطوال أضلاع مثلث، حدد المجموعة التي لا تنتمي للمجموعات الأخرى، فسر إجابتك.

^٢٥ = ^٢٤ + ^٢٣

٢٥ = ١٦ + ٩

إذاً المثلث قائم الزاوية.

^٢٣٧ = ^٢١٢ + ^٢٣٥

١٣٦٩ = ١٤٤ + ١٢٢٥ = ١٣٦٩

إذاً المثلث قائم الزاوية.

^٢٧ = ^٢٥ + ^٢٣

٤٩ $\ne$٢٥ + ٩

إذاً المثلث ليس قائم الزاوية.

١٠، ٨، ٦ هي مضاعفات لـ ٥، ٤، ٣

إذاً المثلث الذي أطوال أضلاعه ١٠، ٨، ٦ هو مثلث قائم الزاوية، المجموعة التي لا تنتمي للمجموعات الأخرى هي: ٣، ٥، ٧

١٧) تحد: وضع سلم طوله ٦ أمتار على حائط رأسي ارتفاعه ٦ ‌أمتار، كم تبعد حافة السلم العليا عن أعلى الحائط إذا كان أسفل السلم يبعد ١,٥ متر من قاعدة الحائط؟ برر إجابتك،

نجد أولاً المسافة بين حافة السلم العليا وأسفل الحائط باستخدام نظرية فيثاغورس.

ج^٢ = أ^٢ + ب^٢

^٢٦ = أ^٢ + ^٢١,٥

أ^٢ = ^٢٦ - ^٢١,٥

أ = $\sqrt{\mathrm{٣٦} - \mathrm{٢٥},\mathrm{٢}}$

أ = ٥,٨ م.

إذاً حافة السلم العليا تبعد عن أعلى الحائط مسافة ٦ - ٥,٨ = ٠,٢ متراً = ٢٠ سم.

١٨) اكتب: طول وتر مثلث قائم الزاوية متطابق الضلعين يساوي $\sqrt{\mathrm{٢٨٨}}$ وحدة، بين كيف تجد طول كل ساق من ساقيه.

ج = $\sqrt{\mathrm{٢٢٨}}$

بما أن المثلث متطابق الضلعين فإن أ = ب

أ = $\sqrt{\frac{\mathrm{٢٨٨}}{\mathrm{٢}}}$

أ = $\sqrt{\mathrm{١٤٤}}$

أ = ب = ١٢ وحدة.

١٩) صمم بدر حديقة منزله على شكل مستطيل، ويخطط لعمل ممر بشكل قطري، كما في الشكل أدناه، أي القياسات الآتية أقرب إلى طول الممر؟

,

أ) ٨ م

ب) ١١م

جـ) ١٧ م

د) ٢٣م

ج^٢ = ^٢١٥ + ^٢٧,٥

ج = ١٦,٧ م.

٢٠) يمثل الشكل أدناه منطاداً هوائياً، أوجد ارتفاعه عن سطح الأرض.

أ) ٥٥ م

ب) ٩٥,٣ م

جـ) ١٢٣ م

د) ١٦٣,٥ م

^٢١١٠ = ^٢٥٥ + ب^٢

ب^٢ = ^٢١١٠ - ^٢٥٥