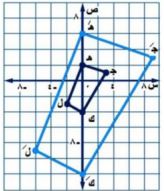
أوجد إحداثيات رؤوس المضلع هـَ جـَ كَ لَ الناتج عن تمدد المضلع هـ جـ ك ل باستعمال كل عامل مقياس فيما يأتي، ثم مثل بيانياً المضلعين هـ جـ ك ل، هـَ جـَ كَ لَ.

هـ(٠، ٢)، جـ(٣، ١)، ك(٠، ٤)، ل(-٢، -٣)، وعامل المقياس = ٣.

• هـ(٠، ٢) $\leftarrow$ هـَ (٠ × ٣، ٢× ٣) $\leftarrow$ هـَ (٠، ٦).
• جـ(٣، ١) $\leftarrow$ جـَ (٣ × ٣، ١× ٣) $\leftarrow$ جـَ (٩، ٣).
• ك(٠، ٤) $\leftarrow$ كَ (٠ × ٣، -٤× ٣) $\leftarrow$ كَ (٠، -١٢).
• ل(-٢، -٣) $\leftarrow$ لَ(-٢ × ٣، -٣× ٣) $\leftarrow$ لَ(-٦، -٩).

هـ(-٢، ٢)، جـ(٤، ٤)، ك(٧، -٢)، ل(-٢، -٤)، وعامل المقياس = $\frac{\mathrm{١}}{\mathrm{٢}}$.

• هـ(-٦، ٢) $\leftarrow$ هـَ (-٦ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ هـَ (-٣، ١).
• جـ(٤، ٤) $\leftarrow$ جـَ (٤ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ جـَ (٢، ٢).
• ك(٧، -٢) $\leftarrow$ كَ (٧ × $\frac{\mathrm{١}}{\mathrm{٢}}$، -٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ كََ(٣.٥، ١).
• ل(-٢، -٤) $\leftarrow$ لَ(-٢ × $\frac{\mathrm{١}}{\mathrm{٢}}$، -٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ لَ(-١، -٢).

حل أسئلة تدرب وحل المسائل

انسخ كل شكل مما يأتي على ورقة مربعات، ثم ارسم صورة تمدده مستعملاً المعلومات الآتية:

٧) المركز: س، وعامل المقياس $\frac{\mathrm{٧}}{\mathrm{٣}}$.

• نرسم من س نصف مستقيم على طول القطعة س ص ونعين عليه النقطة صَ، بحيث يكون س صَ = $\frac{\mathrm{٧}}{\mathrm{٣}}$ س ص = $\frac{\mathrm{٧}}{\mathrm{٣}}$ × ٥,٤ = ١٢,٦(حسبنا طول س ص من فيثاغورس بتشكيل مثلث ٥، ٢).
• نرسم من س نصف مستقيم على طول القطعة س ع ونعين عليه النقطة عَ.

بحيث يكون س عَ = $\frac{\mathrm{٧}}{\mathrm{٣}}$ س ع = $\frac{\mathrm{٧}}{\mathrm{٣}}$ × ٣ = ٧

٨) المركز: ع، وعامل المقياس $\frac{\mathrm{٢}}{\mathrm{٣}}$.

• نرسم من ع نصف مستقيم على طول القطعة ع ص ونعين عليه النقطة صَ، بحيث يكون ع صَ = $\frac{\mathrm{٢}}{\mathrm{٣}}$ س ص = $\frac{\mathrm{٢}}{\mathrm{٣}}$ × ٥,١ = ٣,٤ (حسبنا طول س ص من فيثاغورس بتشكيل مثلث ٥، ١).
• نرسم من ع نصف مستقيم على طول القطعة ع س ونعين عليه النقطة سَ.

بحيث يكون س عَ = $\frac{\mathrm{٧}}{\mathrm{٣}}$ ع س = $\frac{\mathrm{٢}}{\mathrm{٣}}$ × ٣ = ٢

٩) المركز: ل، وعامل المقياس $\frac{\mathrm{٣}}{\mathrm{٤}}$.

• نرسم من ل نصف مستقيم على طول القطعة ل ر ونعين عليه النقطة رَ، بحيث يكون ل رَ = $\frac{\mathrm{٣}}{\mathrm{٤}}$ ل ر = $\frac{\mathrm{٣}}{\mathrm{٤}}$ × ٤ = ٣
• نرسم من ل نصف مستقيم على طول القطعة ل م ونعين عليه النقطة مَ.

بحيث يكون ل مَ = $\frac{\mathrm{٣}}{\mathrm{٤}}$ ل م = $\frac{\mathrm{٣}}{\mathrm{٤}}$ × ٤ = ٣

• نرسم من ل نصف مستقيم على طول القطعة ل ب ونعين عليه النقطة بَ، بحيث يكون ل بَ = $\frac{\mathrm{٣}}{\mathrm{٤}}$ ل ب = $\frac{\mathrm{٣}}{\mathrm{٤}}$ × ٥,٤ = ٤,٠٥ (حسبنا طول ل ب من فيثاغورس بتشكيل مثلث قائماه ٥، ٢).
• نرسم من ل نصف مستقيم على طول القطعة ل ن ونعين عليه النقطة نَ.

بحيث يكون ل نَ = $\frac{\mathrm{٣}}{\mathrm{٤}}$ ل ن = $\frac{\mathrm{٣}}{\mathrm{٤}}$ × ٥ = ٣.٧٥ (حسبنا طول ل ن من فيثاغورس بتشكيل مثلث قائماه ٣، ٤).

١٠) المركز: ن، وعامل المقياس ٢.

• نرسم من ن نصف مستقيم على طول القطعة ن ر ونعين عليه النقطة رَ، بحيث يكون ن رَ = ٢ ن ر = ٢ × ٤,١ = ٨,٢ (حسبنا طول ن ر من فيثاغورس بتشكيل مثلث قائماه ٤، ١).
• نرسم من ن نصف مستقيم على طول القطعة ن م ونعين عليه النقطة مَ.

بحيث يكون ن مَ = ٢ ن م = ٢ × ٣ = ٦

• نرسم من ن نصف مستقيم على طول القطعة ن ب ونعين عليه النقطة بَ، بحيث يكون ن بَ = ٢ ل ب = ٢ × ٢,٨ = ٥,٦ (حسبنا طول ل ب من فيثاغورس بتشكيل مثلث قائماه ٢، ٢).
• نرسم من ن نصف مستقيم على طول القطعة ن ل ونعين عليه النقطة لَ.

بحيث يكون ن لَ = ٢ ن ل = ٢ × ٥ = ١٠ (حسبنا طول ل ن من فيثاغورس بتشكيل مثلث قائماه ٣، ٤).

أوجد إحداثيات رؤوس المضلع هـَ جـَ كَ لَ الناتج عن تمدد المضلع هـ جـ ك ل باستعمال كل عامل مقياس فيما يأتي، ثم مثل بيانياً المضلعين هـ جـ ك ل، هـَ جـَ كَ لَ.

١١) هـ(٠، ٢)، جـ(٣، ١)، ك(٠، ٤)، ل(-٢، -٣)، وعامل المقياس = ٣.

• هـ(٠، ٢) $\leftarrow$ هـَ (٠ × ٣، ٢× ٣) $\leftarrow$ هـَ (٠، ٦).
• جـ(٣، ١) $\leftarrow$ جـَ (٣ × ٣، ١× ٣) $\leftarrow$ جـَ (٩، ٣).
• ك(٠، ٤) $\leftarrow$ كَ (٠ × ٣، -٤× ٣) $\leftarrow$ كَ (٠، -١٢).
• ل(-٢، -٣) $\leftarrow$ لَ(-٢ × ٣، -٣× ٣) $\leftarrow$ لَ(-٦، -٩).

١٢) هـ(-٢، ٢)، جـ(٤، ٤)، ك(٧، -٢)، ل(-٢، -٤)، وعامل المقياس = $\frac{\mathrm{١}}{\mathrm{٢}}$.

• هـ(-٦، ٢) $\leftarrow$ هـَ (-٦ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ هـَ (-٣، ١).
• جـ(٤، ٤) $\leftarrow$ جـَ (٤ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ جـَ (٢، ٢).
• ك(٧، -٢) $\leftarrow$ كَ (٧ × $\frac{\mathrm{١}}{\mathrm{٢}}$، -٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ كََ(٣.٥، ١).
• ل(-٢، -٤) $\leftarrow$ لَ(-٢ × $\frac{\mathrm{١}}{\mathrm{٢}}$، -٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ لَ(-١، -٢).

إذا علمت أن أحد المضلعين في كل رسم مما يأتي هو تمدد للمضلع الآخر، فأوجد عامل مقياس كل تمدد، وصنفه فيما إذا كان تكبيراً أو تصغيراً.

١٣)

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{جـَ}}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{جـ}}=\frac{\mathrm{٣}}{\mathrm{٥}}$

بما أن عامل المقياس = $\frac{\mathrm{٣}}{\mathrm{٥}}$ < ١ فالتمدد تصغير.

١٤)

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{جـَ}}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{جـ}}=\frac{\mathrm{٩}}{\mathrm{٦}}=\frac{\mathrm{٣}}{\mathrm{٢}}$

بما أن عامل المقياس = $\frac{\mathrm{٣}}{\mathrm{٢}}$ > ١ فالتمدد تكبير.

١٥)

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} بَ}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} ب}=\frac{\mathrm{٢}}{\mathrm{١}}$ = ٢

١٦)

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{هـَ}}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{هـ}}=\frac{\mathrm{٢}}{\mathrm{٥}}$

بما أن عامل المقياس = $\frac{\mathrm{٢}}{\mathrm{٥}}$ < ١ فالتمدد تصغير.

١٧) تصميم: لوضع صورة في مجلة، يقوم المصمم بتصغير الصورة وفق عامل مقياس $\frac{\mathrm{٣}}{\mathrm{١٠}}$، فما أبعاد صورة وضعها المصمم إذا كان طولها الأصلي ١٥ سم، وعرضها الأصلي ١٠ سم؟

• طول الصورة على الشاشة = عامل المقياس × طول الصورة الأصلية.
• طول الصورة على الشاشة = ٣,٥ × ٤ = ١٤ سم.
• عرض الصورة على الشاشة = عامل المقياس × عرض الصورة الأصلية.
• عرض الصورة على الشاشة = ٣,٥ × ٤ = ١٠,٥ سم.

بعدا الصورة على الجهاز (١٤ سم × ١٠,٥ سم).

١٨) جهاز العرض: يستعمل جهاز العرض في عرض الصور المرسومة على شفافيات على شاشة، بحيث تكون مكبرة وفق عامل مقياس يساوي ٣,٥، إذا كان طول الصورة الأصلية ١٥ سم، وعرضها الأصلي ١٠ سم؟

• طول الصورة على الشاشة = عامل المقياس × طول الصورة الأصلية.
• طول الصورة على الشاشة = $\frac{\mathrm{٣}}{\mathrm{١٠}}$ × ١٥ = ٤,٥ سم.
• عرض الصورة على الشاشة = عامل المقياس × عرض الصورة الأصلية.
• عرض الصورة على الشاشة = $\frac{\mathrm{٣}}{\mathrm{١٠}}$ × ١٠ = ٣ سم.

بعدا الصورة على الجهاز (٤,٥ سم × ٣ سم)

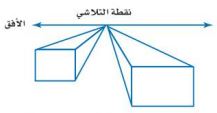
رسم: للسؤالين ١٩، ٢٠ استعمل المعلومات الآتية:

يستعمل الرسامون التمدد في إنشاء مسافات أو أعماق وهمية، فمثلاً عندما تقف على الرصيف وتنظر إلى نهاية الشارع فإن جانبي الشارع المتوازيين يظهران كأنهما يتقربان تدريجياً حتى يلتقيا في نقطة تسمى نقطة التلاشي.

١٩) أي الشكلين في الرسم يبدو أقرب؟ وضح إجابتك.

الشكل الأيمن هو الأقرب حيث يبدو المستطيل فيه أكبر والخطوط التي تصل بين المستطيل ونقطة التلاشي أطول من نظيراتها في الشكل الأيسر.

٢٠) ارسم شكلاً مشابهاً للشكل المجاور، قس طول المستطيل الأكبر، ثم ارسم شكلاً آخر مشابهاً له، بحيث تكون قياساته تساوي $\frac{\mathrm{٧}}{\mathrm{٥}}$ الشكل الأصلي.

• نبدأ من نقطة التلاشي ونرسم خطوط الشكل الجديد بحيث يكون كل خط يعادل $\frac{\mathrm{٧}}{\mathrm{٥}}$ × طول نظيره في الشكل الأصلي.
• ثم من نهايات الخطوط نرسم المستطيل بحيث تكون أبعاده $\frac{\mathrm{٧}}{\mathrm{٥}}$ × أبعاد نظيره في الشكل الأصلي.

٢١) مسألة مفتوحة: مثل بيانياً مثلثاً وصورة له بعد إجراء تمدد عامل مقياسه أكبر من ١، ثم مثل الصورة بيانياً بعد إجراء تمدد عامل مقياسه أصغر من ١، توقع قيمة عامل المقياس للتمدد من الشكل الأصلي إلى الشكل الأخير، وضح السبب، ثم تحقق من صحة توقعك.

نختار النقطة أ (٢، ٢) من الشكل الأصلي والنقطة أَ (١، ١) من الشكل الأخير (الأصغر).

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} أ َ}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} أ}=\frac{\mathrm{١}}{\mathrm{٢}}$

أي أن أبعاد الشكل الأخير وإحداثياته تعادل $\frac{\mathrm{١}}{\mathrm{٢}}$ مقابلاتها من الشكل الأصلي.

يمكننا التحقق بأخذ نقاط أخرى مثل النقطتان المتناظرتان: ب (٦، ٤) من الشكل الأصلي، بَ (٣، ٢) من الشكل الأخير (الأصغر).

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} بَ}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} ب}=\frac{\mathrm{٣}}{\mathrm{٦}}=\frac{\mathrm{١}}{\mathrm{٢}}$ التوقع صحيح.

٢٢) تحد: صف الصورة الناتجة عن تمدد شكل ما بعامل مقياس قيمته (-٢).

إذا كان الشكل في الربع الأول من محور الإحداثيات $\leftarrow$ الإحداثي السيني والصادي موجبان $\leftarrow$ بعد الضرب بعامل المقياس - ٢ $\leftarrow$ سيصيب الإحداثي السيني والصادي سالبان وأكبر قيمة $\leftarrow$ الصورة الناتجة تقع في الربع الثالث $\leftarrow$ الصور الناتجة مثلي حجم الصورة الأصلية وناتجة عن دوران الصورة الأصلية حول مركز الإحداثيات ١٨٠°.

٢٣) اكتب قاعدة عامة لإيجاد الإحداثيات الجديدة للزوج المرتب (س، ص) بعد إجراء تمدد عامل مقياسه يساوي ك.

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{الجديدة}}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} \mathrm{الأصلية}}=\frac{\mathrm{الإحداثي} \mathrm{الصادي} \mathrm{للنقطة} \mathrm{الجديدة}}{\mathrm{الإحداثي} \mathrm{الصادي} \mathrm{للنقطة} \mathrm{الأصلية}}$

ك = $\frac{سَ}{س}=\frac{صَ}{ص}\leftarrow$سَ = ك × س

صَ = ك × ص $\leftarrow$ الإحداثيات الجديدة (ك × س، ك، ص).

٢٤) في الشكل أدناه، إذا كان المربع س يشابه المربع ص:

فأوجد عامل المقياس المستعمل لتمدد المربع س إلى المربع ص.

أ) $\frac{\mathrm{١}}{\mathrm{٧}}$

ب) $\frac{\mathbf{٣}}{\mathbf{٥}}$

جـ) $\frac{\mathrm{٥}}{\mathrm{٣}}$

د) ٧

عامل مقياس التمدد = $\frac{\mathrm{طول} \mathrm{ضلع} \mathrm{المربع} \mathrm{الجديد}}{\mathrm{طول} \mathrm{ضلع} \mathrm{المربع} \mathrm{الأصلي}}=\frac{ص}{س}=\frac{\mathrm{٢١}}{\mathrm{٣٥}}=\frac{\mathrm{٣}}{\mathrm{٥}}$

٢٥) يمثل الشكل أ ب جـ د تمدداً للشكل الرباعي س ص ع ل:

أي الأعداد التالية يمثل أفضل عامل مقياس تمدد استعمل لتحويل الشكل الرباعي أ ب جـ د إلى الشكل الرباعي س ص ع ل؟

أ) $\frac{\mathbf{١}}{\mathbf{٢}}$

ب) $\frac{\mathrm{١}}{\mathrm{٣}}$

جـ) ٢

د) ٣

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{للنقطة} ع}{\mathrm{الإحداثي} \mathrm{السينين} \mathrm{للنقطة} \mathrm{جـ}}=\frac{\mathrm{٢}}{\mathrm{٤}}=\frac{\mathrm{١}}{\mathrm{٢}}$