حلول الأسئلة
السؤال
يصنع تركي نموذجاً لأطول الجسور المبينة في الجدول التالي، حيث يشير كل سنتمتر في النموذج إلى ٣٠ متراً، فما طول النموذج بالسنتمتر؟
الحل
| جسور | |
| الجسر | الطول (متر) |
| ١ | ١٢٠٠ |
| ٢ | ١٠٥٤ |
| ٣ | ٧٠٠ |
معطيات المسألة:
كل سنتيمتر في النموذج يشير إلى ٣٠ متر.
المطلوب: طول النموذج بالسنتيمتر.
استعمل خطة أنشئ نموذجاً لأحل المسألة.
طول الجسر١ = ١٢٠٠ ÷ ٣٠ = ٤٠ سنتمتر.
طول الجسر٢ = ١٠٥٤ ÷ ٣٠ = ٣٥,١٣٣٣ سنتمتر.
طول الجسر٣ = ٧٠٠ ÷ ٣٠ = ٢٣,٣٣٣٣ سنتمتر.
الجسر١:
١سم ٣٠متر.
٤٠سم س
س = ٤٠ × ٣٠ = ١٢٠٠ متراً.
الجسر٢:
١سم ٣٠متر.
٣٥,١٣٣٣سم ص
ص = ٣٥,١٣٣٣ × ٣٠ = ١٠٥٤ متراً.
الجسر٣:
١سم ٣٠متر.
٢٣,٣٣٣٣سم ع
ع = ٢٣,٣٣٣٣ × ٣٠ = ٧٠٠ متراً، إذاً الإجابة صحيحة.
مشاركة الحل
الدرس الرابع: خطة حل المسألة
ارجع إلى المسألة السابقة، ثم أجب عن الأسئلة ١-٤:
١) فسر لماذا استعملت خطة إنشاء نموذج لإيجاد أقل عدد من الطاولات.
لأنها أسهل خطة لإيجاد الحل.
٢) اشرح خطة أخرى يمكن استعمالها لحل المسألة.
خطة التبرير المنطقي: الطاولة البيضاوية تكفي لجلوس ١٠ مدعوين
إذاً يتبقى ٢٢-١٠= ١٢ مدعو يجلسون على الطاولات المربعة، وكل طاولة مربعة تكفي لجلوس ٤ مدعوين.
إذاً نحتاج إلى ١٢÷٤=٣ طاولات مربعة.
٣) افترض أن عدد المدعوين ٣٠ شخصاً، فكم طاولة مربعة الشكل يحتاج إليها فارس؟
٣٠-١٠=٢٠
إذاً نحتاج إلى ٢٠÷٤=٥ طاولة مربعة، إذاً يحتاج فارس إلى ٥ طاولات مربعة.
٤) تحقق من إجابتك للمسألة ٣.
١٠+(٥×٤) = ١٠+٢٠=٣٠ شخصاً، إذاً الإجابة صحيحة.
استعمل خطة إنشاء نموذج لحل المسائل التالية:
٥) فتحت سمية ٨ علب صلصال، إذا كان في كل علبة ٤ قطع من الصلصال الرمادي، ونصف هذا العدد من قطع الصلصال الأحمر، فما عدد قطع الصلصال الأحمر والرمادي في العلب الثمانية؟
معطيات المسألة:
- ٨ علب صلصال.
- في كل علبة ٤ قطع من الصلصال الرمادي، ٢ قطعة من الصلصال الأحمر.
المطلوب: عدد قطع الصلصال الأحمر والرمادي في العلب الثمانية.
استعمل خطة أنشئ نموذجاً لأحل المسألة.
عدد قطع الصلصال الأحمر = ٢ × ٨ =١٦ قطعة.
عدد قطع الصلصال الرمادي = ٤ × ٨ = ٣٢ قطعة.
عدد قطع الصلصال الأحمر١٦قطعة، وفي كل علبة ٢ قطعة.
إذاً عدد علب الصلصال =١٦÷ ٢ = ٨ علبة.
عدد قطع الصلصال الرمادي = ٣٢ قطعة، وفي كل علبة ٤ قطع.
إذاً عدد علب الصلصال = ٣٢ ÷ ٤ = ٨ علبة.
إذاً الإجابة صحيحة.
٦) يصنع تركي نموذجاً لأطول الجسور المبينة في الجدول التالي، حيث يشير كل سنتمتر في النموذج إلى ٣٠ متراً، فما طول النموذج بالسنتمتر؟
| جسور | |
| الجسر | الطول (متر) |
| ١ | ١٢٠٠ |
| ٢ | ١٠٥٤ |
| ٣ | ٧٠٠ |
معطيات المسألة:
كل سنتيمتر في النموذج يشير إلى ٣٠ متر.
المطلوب: طول النموذج بالسنتيمتر.
استعمل خطة أنشئ نموذجاً لأحل المسألة.
طول الجسر١ = ١٢٠٠ ÷ ٣٠ = ٤٠ سنتمتر.
طول الجسر٢ = ١٠٥٤ ÷ ٣٠ = ٣٥,١٣٣٣ سنتمتر.
طول الجسر٣ = ٧٠٠ ÷ ٣٠ = ٢٣,٣٣٣٣ سنتمتر.
الجسر١:
١سم٣٠متر.
٤٠سمس
س = ٤٠ × ٣٠ = ١٢٠٠ متراً.
الجسر٢:
١سم٣٠متر.
٣٥,١٣٣٣سمص
ص = ٣٥,١٣٣٣ × ٣٠ = ١٠٥٤ متراً.
الجسر٣:
١سم٣٠متر.
٢٣,٣٣٣٣سمع
ع = ٢٣,٣٣٣٣ × ٣٠ = ٧٠٠ متراً، إذاً الإجابة صحيحة.
٧) القياس: يريد فؤاد أن يدهن ثلاثة جدران متطابقة في غرفته، إذا كان طول الجدار ٥ أمتار، وعرضه ٣ أمتار، وكانت علبة الدهان الواحدة تكفي لدهان ١٥ متراً مربعاً، فكم علبة دهان يحتاج إليها؟
معطيات المسألة:
- ٣ جدران.
- طول الجدار ٥ أمتار وارتفاعه ٣ أمتار.
- علبة الدهان تكفي لدهان ١٦ متراً مربعاً.
المطلوب: كم علبة دهان يحتاج إليها.
استعمل خطة أنشئ نموذجاً لأحل المسألة.
مساحة الجدار الأول = ٣×٥ = ١٥ متر مربع.
مساحة الجدار الثاني = ٣×٥ = ١٥ متر مربع.
مساحة الجدار الثالث = ٣×٥ = ١٥ متر مربع.
إذاً نحتاج إلى ٣ علب دهان تقريباً.
٣ علب دهان تكفي لدهان ١٦+١٦+١٦ = ٤٨ متر مربع.
مجموع مساحات الجدران الثلاثة = ١٥+١٥+١٥ = ٤٥ متر مربع.
إذاً الإجابة صحيحة.
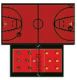
٨) القياس: يركض رياض كل يوم ٣٢٠٠ متر حول ملعب المدرسة الموضح بالشكل أدناه. كم دورة يركض حول الملعب؟
معطيات المسألة:
- يركض رياض ٣٢٠٠ متر حول الملعب.
- الدورة الواحدة =٤٠٠متراً.
المطلوب: كم دورة يركض حول الملعب.
استعمل خطة أنشئ نموذجاً لأحل المسألة
عدد الدورات التي يركض بها =٣٢٠٠÷٤ = ٨دورات.
الدورة الواحدة =٤٠٠متر.
إذاً ٨ دورات = ٨×٤٠٠ = ٣٢٠٠ متراً.
إذاً الإجابة صحيحة.
٩) طول ملعب كرة الطائرة ١٨ متراً، وعرضه ٩ أمتار، وطول ملعب كرة السلة ٢٩ متراً، وعرضه ١٥ متراً. كم ملعب كرة طائرة يمكن إنشاؤه في ملعب مرة السلة؟
- طول ملعب كرة الطائرة ١٨متراً وعرضه ٩أمتار.
- طول ملعب كرة السلة ٢٩متراً وعرضه ١٥متراً.
المطلوب: كم ملعب كرة طائرة يمكن إنشاؤه في ملعب كرة السلة؟
استعمل خطة أنشئ نموذجاً لأجد حل المسألة.
مساحة ملعب كرة الطائرة = ١٨×٩ = ١٦٢ متر مربع.
مساحة ملعب كرة السلة = ٢٩×١٥ = ٤٣٥متر مربع.
إذاً ٤٣٥ ÷ ١٦٢ = ٢,٦٨ملعب.
إذاً يمكن إنشاء ٢ ملعب كرة طائرة في ملعب كرة السلة ٤٣٥ - ١٦٢ = ٢٧٣
٢٧٣ - ١٦٢ = ١١١ إذاً الإجابة صحيحة.
١٠) .JPG) نظم متجر أحد الأصناف على شكل هرم. إذا كان في الطبقة السفلى منه ٤ صناديق، وكان هناك ٤ طبقات، ويقل عدد الصناديق في كل طبقة بمقدار صندوق واحد عن صناديق الطبقة السابقة. السؤال المرتبط بهذا الصنف الذي تكون إجابته ١٠؟
نظم متجر أحد الأصناف على شكل هرم. إذا كان في الطبقة السفلى منه ٤ صناديق، وكان هناك ٤ طبقات، ويقل عدد الصناديق في كل طبقة بمقدار صندوق واحد عن صناديق الطبقة السابقة. السؤال المرتبط بهذا الصنف الذي تكون إجابته ١٠؟
- في الطبقة السفلى ٤ صناديق، ويوجد ٤ طبقات
- يقل عدد الصناديق في كل طبقة عن الطبقة السابقة بمقدار صندوق.
المطلوب: ما السؤال المرتبط بهذا الصنف الذي تكون إجابته ١٠؟
استعمل خطة أنشئ نموذجاً لأجد حل المسألة.
كم مجموع الصناديق في الأربع طبقات
مجموع الصناديق في الأربع طبقات = ٤ + ٣ + ٢ + ١ = ١٠ إذاً الإجابة صحيحة.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)