اختبار منتصف الفصل
في كل علاقة مما يأتي، حدد ما إذا كانت y تمثل دالة في x:
1) 3x+7y=21
دالة.
2)
دالة.
3)
ليست دالة.
4)
دالة.
5) إذا كانت ، فأوجد f(2).
f(2)=2
6) كرة قدم: يعطى ارتفاع كرة قدم عن سطح الأرض عند ضربها من قبل حارس مرمى بالدالة h(t)=-8t2+50t+5، حيث h ارتفاع الكرة بالأقدام، وt الزمن بالثواني.
a) أوجد ارتفاع الكرة بعد 3 ثوان.
b) ما مجال هذه الدالة؟ برر إجابتك.
(2.55, 0] حيث أن الزمن والارتفاع لا يمكن أن يكون أحد منهما سالب.
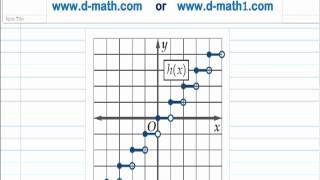
استعمل التمثيل البياني للدالة h أدناه لإيجاد مجالها ومداها في كل مما يأتي:
7)
- المجال=
- المدى=
8)
- المجال=
- المدى=
أوجد المقطع y والأصفار لكل من الدالتين الآتيتين:
9) f(x)=x3-16x
لإيجاد المقطع y نضع x=0، f(x)=0 المقطع y=0
لإيجاد الأصفار:
10)
لإيجاد المقطع y نضع x=0
f(x)=5-0=5 المقطع y=5
لإيجاد لأصفار نضع f(x)=0
اختبر تماثل كل من المعادلتين الآتيتين حول المحور x، والمحور y، ونقطة الأصل.
11) x2+y2=9
المنحنى متماثل حول نقطة الأصل لأن:
المنحنى متماثل حول المحور x لأن:
المنحنى متماثل حول المحور y لأن:
12) xy=4
المنحنى متماثل حول نقطة الأصل لأن:
المنحنى غير متماثل حول المحور x لأن:
المنحنى غير متماثل حول المحور y:
حدد ما إذا كانت كل من الدالتين الآتيتين متصلة عند 5 = x. وبرر إجابتك باستعمال اختبار الاتصال.
13)
الدالة غير متصلة لأن الدالة غير معرفة عند x=5.
14)
الدالة متصلة عند x=5 وقيمتها 2.5
من الطرفين
إذن الدالة متصلة عند x=5
صف سلوك طرفي كل من التمثيلين البيانيين الآتيين، ثم عزز إجابتك عددياً.
15)
يتضح من التمثيل البياني أنه عندما وعندما
16)
يتضح من التمثيل البياني أنه عندما وعندما
17) اختيار من متعدد: ما نوع نقطة عدم الاتصال للدالة الممثلة في الشكل أدناه عند x=1.5؟
- غير معرف.
- لا نهائي.
- قفزي.
- قابل للإزالة.
استعمل التمثيل البياني لكل دالة أدناه لتقدير الفترات التي تكون فيها الدالة متزايدة أو متناقصة أو ثابتة مقربة إلى أقرب 0.5 وحدة، وعزز إجابتك عددياً.
18)
متزايدة في الفترة ، ومتناقصة في الفترة
19)
متزايدة في الفترة ومتناقصة في الفترة (1.5, 2-) ومتزايدة في الفترة .
20) استعمل التمثيل البياني للدالة في السؤال 18 أعلاه، وقدر قيمة x التي يكون للدالة عندها قيمة قصوى مقربة إلى أقرب 0.5 وحدة، وأوجد قيمة الدالة عندها، وبين نوعها، ثم عزز إجابتك عددياً.
- يوضح التمثيل البياني في السؤال (18) أن للدالة f(x) قيمة صغرى محلية ومقدارها 4- عند x=3.
- يوضح التمثيل البياني في السؤال (19) أن للدالة f(x) قيمة عظمى محلية ومقدارها 2 عند x=-1، كما توجد قيمة صغرى محلية عند x=1 ومقدارها -2
21) فيزياء: إذا كانت المسافة التي يقطعها جسم ساقط من مكان مرتفع تعطى بالدالة d(t)=16t2، حيث t الزمن بالثواني و d(t) المسافة المقطوعة بالأقدام إذا أهملت مقاومة الهواء فأوجد متوسط السرعة في الفترة [0,3].
مشاركة الدرس
الاختبارات
اختبار الكتروني: اختبار منتصف الفصل
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات