حل أسئلة تدرب وحل المسائل
أوجد مساحة كل مثلث فيما يأتي:
٥- .JPG)
ق = ٦ وحدات، ع = ٨ وحدات.
م = ق ع مساحة المثلث.
= (٦) (٨) ضع ٦ بدلاً من ق، ٨ بدلاً من ع.
= (٤٨) اضرب.
= ٢٤ وحدة٢
٦- .JPG)
ق = ٥ وحدات، ع = ٣ وحدات.
م = ق ع مساحة المثلث.
= (٥) (٣) ضع ٥ بدلاً من ق، ٣ بدلاً من ع.
= (١٥) اضرب.
= ٧,٥ وحدة٢
٧- .JPG)
م = ق ع مساحة المثلث.
= (٩) (١٠) ضع ٩ بدلاً من ق، ١٠ بدلاً من ع.
= (٩٠) اضرب.
= ٤٥ ملم٢
٨- 
م = ق ع مساحة المثلث.
= (٢٤,٨) (١٦) ضع ٢٤,٨ بدلاً من ق، ١٦ بدلاً من ع.
= (٣٩٦,٨) اضرب.
= ١٩٨,٤ سم٢
٩- 
م = ق ع مساحة المثلث.
= (٢٥) (٧) ضع ٢٥ بدلاً من ق، ٧ بدلاً من ع.
= (١٧٥) اضرب.
= ٨٧,٥ كلم٢
١٠- 
م = ق ع مساحة المثلث.
= (٤١,٥) (٣٦) ضع ٤١,٥ بدلاً من ق، ٣٦ بدلاً من ع.
= (١٤٩٤) اضرب.
= ٧٤٧ م٢
١١- الارتفاع ١٤م وطول القاعدة ٣٥م.
م = ق ع مساحة المثلث.
= (٣٥) (١٤) ضع ٣٥ بدلاً من ق، ١٤ بدلاً من ع.
= (٤٩٠) اضرب.
= ٢٤٥ م٢
١٢- الارتفاع ٢٧ سم وطول القاعدة ١٩سم.
م = ق ع مساحة المثلث.
= (١٩) (٢٧) ضع ١٩ بدلاً من ق، ٢٧ بدلاً من ع.
= (٥١٣) اضرب.
= ٢٥٦,٥ م٢
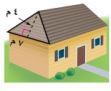
١٣- مساكن: يريد صاحب البيت المجاور أن يغطي المنطقة المثلثة الشكل من السقف بألواح خشبية ما مساحة الخشب الذي يغطي هذه المنطقة؟
م = ق ع مساحة الخشب الذي يغطي المنطقة.
= (٧) (٤) ضع ٧ بدلاً من ق، ٤ بدلاً من ع.
= (٢٨) اضرب.
= ١٤ م٢
١٤- هندسة: يريد مهندس معماري أن يعمل تصميماً لبناء على قطعة أرض مثلثية فإذا كان طول القاعدة القطعة ١٠٠,٨ م وارتفاعها ٩٦,٣م فأوجد مساحتها.
م = ق ع مساحة قطعة الأرض المثلثية.
= (١٠٠,٨) (٩٦,٣) ضع ١٩ بدلاً من ق، ٢٧ بدلاً من ع.
= (٩٧٠٧,٠٤) اضرب.
= ٤٨٥٣,٥٢ م٢
١٥- أحواض أزهار: أوجد مساحة الأزهار الموضح في الشكل المقابل وإذا كان الكيس الواحد من التربة الجاهزة يكفي تغطية نصف متر مربع من الحوض فما عدد الأكياس اللازمة لتغطية حوض الأزهار كاملاً؟
م = ق ع مساحة حوض الأزهار.
= (٣) (٢) ضع ٣ بدلاً من ق، ٢ بدلاً من ع.
= (٦) اضرب.
= ٣ م٢
الكيس الواحد يكفي لتغطية نصف متر مربع إذن عدد الأكياس اللازمة لتغطية حوض الأزهار كاملاً.
= ٣ ÷ ٠,٥
= ٦ أكياس.
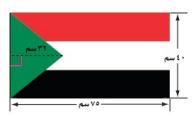
١٦- أعلام: ما مساحة المثلث في علم دولة السودان المجاور؟
م = ق ع مساحة المثلث.
= (٤٠) (٣٢) ضع ٤٠ بدلاً من ق، ٣٢ بدلاً من ع.
= (١٢٨٠) اضرب.
= ٦٤٠ سم٢
أشكال مركبة: أوجد المحيط والمساحة لكل شكل مما يأتي:
١٧- 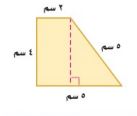
محيط الشكل = مجموع أطوال أضلاعه.
= ٢ + ٤ + ٥ + ٥ = ١٦ سم.
قاعدة المثلث = ٥ - ٢ = ٣ سم.
مساحة الشكل = مساحة المثلث + مساحة المستطيل.
= ق ع + ل ض
= (٣) (٤) + (٤) (٢)
= ٦ + ٨ = ١٤ سم٢
١٨- 
محيط الشكل = مجموع أطوال أضلاعه.
= ١٠ + ٩ + ١٠ + ٦ + ٩ + ٦ = ٥٠ ملم
مساحة الشكل = مساحة المثلث + مساحة المستطيل + مساحة المثلث.
= ق ع + ل ض + ق ع
= (٦) (٨) + (٩) (٨) + (٦) (٨)
= ٢٤ + ٧٢ + ٢٤ = ١٢٠ ملم٢
١٩- اكتشف الخطأ: أوجد كل من فهد وسعد طول قاعدة المثلث المجاور الذي مساحته ١٠٠م٢ أيهما كانت صحيحة؟ فسر إجابتك.
تفسير الإجابة: لأن مساحة المثلث = ق ع وليس ق ع.
تحد: إذا علمت أن المثلثات جميعها متطابقة والمربعات الصغيرة جميعها متطابقة في النمط المقابل فحل الأسئلة ٢٠ - ٢٣:
٢٠- أوجد طول القاعدة أحد المثلثات الصغيرة وارتفاعه.
طول ضلع المربع الصغير = = ٤ سم.
قاعدة المثلث = طول ضلع المربع الصغير = ٤ سم.
ارتفاع المثلث = نصف طول الضلع المربع الصغير = = ٢ سم.
٢١- احسب مساحة كل مثلث ثم أوجد المساحة الكلية للمثلثات جميعها.
مساحة كل مثلث = ق ع = (٤)(٢) = ٤سم٢
المساحة الكلية للمثلثات جميعها = ١٦ × ٤ = ٦٤ سم٢
٢٢- احسب مساحة أحد المربعات الصغيرة ثم احسب المساحة الكلية للمربعات (التي لا يوجد بداخلها مثلثات).
مساحة أحد المربعات الصغيرة = طول الضلع في نفسه.
= ٤ × ٤ = ١٦ سم٢
المساحة الكلية = ٥ × ١٦ = ٨٠ سم٢
٢٣- ما المساحة الكلية للشكل؟ وهل إجابتك معقولة؟
المساحة الكلية للشكل = ١٢ × ١٢ = ١٤٤ سم٢
نعم الإجابة مقبولة.
٢٤- تبرير: إذا كان هناك مثلثان مساحة كل منهما ٢٤ وحدة مربعة فهل لهما طول القاعدة نفسها والارتفاع ذاته دائماً؟ فسر إجابتك.
لا
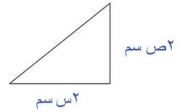
٢٥- اكتب: ارسم مثلثاً واختر زمراً لقاعدته وآخر لارتفاعه ثم ارسم مثلثاً آخر له القاعدة نفسها وارتفاعه يساوي مثلي ارتفاع المثلث الأول ثم أوجد مساحة كل منهما واكتب النسبة بين مساحتيهما.
مساحة المثلث = ق ع
= (٢س) (ص)
= س ص سم٢
النسبة بين مساحتيهما = ٢:١
مساحة المثلث = ق ع
= (س)(٢ص)
= ٢س ص سم٢
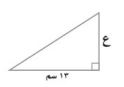
٣٦- قصت سيرين مثلثاً من الورق المقوى لعمل منظر على شكل مثلث قائم الزاوية كالمرسوم أدناه.
إذا كانت مساحة المثلث ٨٤,٥ سم٢ ، فما ارتفاعه؟
أ. ٦,٥ سم
ب. ١٣ سم
جـ. ٢٦ سم
د. ١٦٩ سم
٣٧- يبين الجدول أدناه مساحات مثلثات لها الارتفاع نفسه ولكن تختلف في طول القاعدة.
| مساحات المثلثات | ||
|
الارتفاع (وحدات) |
القاعدة (الارتفاع) |
المساحات (وحدة مربعة) |
| ٧ | ٢ | ٧ |
| ٧ | ٣ | |
| ٧ | ٤ | ١٤ |
| ٧ | ٥ | |
| ٧ | س | ...... |
أي عبارة مما يأتي يمكن استعمالها لإيجاد مساحة مثلث ارتفاعه ٧ وحدات وطول قاعدته س وحدة؟
أ. ٧ س
ب.
جـ.
د.

.JPG)
.JPG)
.JPG)
.JPG)
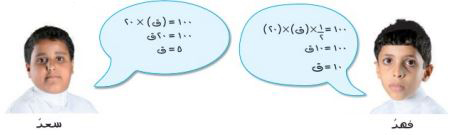
.JPG)
.JPG)
.JPG)
.JPG)
النقاشات