حل أسئلة تدرب وحل المسائل

أوجد حجم كل منشور رباعي فيما يأتي:

٧-

ح= ل ض ع.

= ١٠ × ٤ × ٣

= ١٢٠ م^٣

٨-

ح= ل ض ع.

= ٦ × ٦ × $\frac{\mathrm{٣}}{\mathrm{٤}}\mathrm{٤}$

= $\frac{\mathrm{٦}}{\mathrm{١}}\times \frac{\mathrm{٦}}{\mathrm{١}}\times \frac{\mathrm{١٩}}{\mathrm{٤}}$ = ١٧١ سم^٣

٩-

ح= ل ض ع.

= ١٠ × ٥ × ١٢

= ٦٠٠ م^٣

١٠-

ح= ل ض ع.

= ٧ × ٤ × ٣

= ٨٤ سم٣

١١-

ح = ل ض ع.

= ٢٢ × ٥ × ١٣

= ١٤٣٠ سم^٣

١٢-

ح = ل ض ع.

= ٣٥,٥ × ٢٩,٨ × ٦,٣ = ٦٦٦٤,٧٧ م^٣

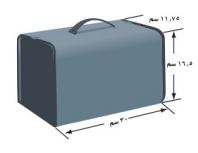
١٣- حقيبة: قدر حجم الحقيبة في الصورة المجاورة.

ح = ل ض ع.

= ٢٠ × ١١,٧٥ × ١١,٥

= ٢٧٠٢,٥ سم^٣

١٤- الكعبة المشرفة: يبلغ ارتفاع الكعبة المشرفة ١٤ م وطولها ١٢م تقريباً وعرضها ١١,٢٥ م تقريباً أوجد حجمها التقريبي.

ح = ل ض ع.

≈ ١٢ × ١١,٢٥ × ١٤

≈ ١٨٩٠ م^٣

١٥- أوجد طول منشور رباعي حجمه ٢٨٣٠,٥ سم^٣ وعرضه ١٧ سم، وارتفاعه ٩سم.

ل = ح ÷ ض ع.

= ٢٨٣٠,٥ ÷ (١٧× ٩)

= ٢٨٣٠,٥ ÷ ١٥٣

= ١٨,٥ سم

١٦- أوجد عرض منشور رباعي طوله ٢٤سم وحجمه ١١٢٣٢ سم^٣ ، وارتفاعه ٣٦سم.

ض = ح ÷ ل ع.

= ١١٢٣٢ ÷ (٢٤×٣٦)

= ١١٢٣٢ ÷ ٨٦٤

= ١٣ سم.

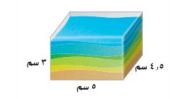
فن الرمل: لحل السؤالين ١٧ - ١٨ استعمل المعلومة الآتية: "الوعاء الزجاجي المجاور فيه رمل إلى ارتفاع ٢,٢٥ سم"

١٧- ما كمية الرمل الموجودة في الوعاء حالياً؟

ح= ل ض ع.

= ٥ × ٤,٥ × ٢,٢٥

= ٥٠,٦٢٥

١٨- ما كمية الرمل الإضافية التي يمكن أن يسعها الوعاء بشكل كامل؟

ح = ل ض ع.

= ٥ × ٤,٥ × ٣

= ٦٧,٥ سم^٣

كمية الرمل الإضافية = حجم الوعاء - كمية الرمل الموجود في الوعاء.

= ٦٧,٥ - ٥٠,٦٢٥

= ١٦,٨٧٥ سم^٣

قارن بين كل مما يأتي مستعملاً (>، <، =)؛ لتحصل على جملة صحيحة:

١٩- ١ سم^٣ < ١ م^٣

٢٠- ١ سم^٣ > ٢٥ ملم^٣

٢١- ٢٧ سم^٣ = ٢٧٠٠٠ ملم^٣

٢٢- الحس العددي: أوجد طول الحرف لمكعب حجمه ٦٤ وحدة مكعبة.

حجم المكعب = طول الحرف × نفسه × نفسه.

= ٦٤ وحدة مكعبة.

= ٤ × ٤ × ٤ وحدة مكعبة.

إذن الارتفاع = ٤ وحدات.

٢٣- تبرير: أيهما أكبر حجماً منشور طوله ٥سم وعرضه ٤سم وارتفاعه ١٠ سم أم منشور طوله ١٠ سم وعرضه ٥ سم وارتفاعه ٤ سم؟ فسر إجابتك.

المنشورين متساويين في الحجم

تفسير الإجابة:

ح١ = ل ض ع.

= ٥ × ٤ × ١٠

= ٢٠٠ سم^٣

ح ٢ = ل ض ع.

= ١٠ × ٥ × ٤

= ٢٠٠ سم^٣

٢٤- تقدير: قدرت أمل حجم منشور طوله ٥,٨ سم وعرضه ٣ سم وارتفاعه ١٢,٢ سم على أنه أصغر من ١٨٠ سنتمتراً مكعباً فهل تقديرها صحيح؟ فسر إجابتك.

لا تفسير الإجابة.

ح = ل ض ق.

= ٥,٨ × ٣ × ١٢,٢

= ٢١٢,٢٨ سم^٣

بما أن ٢١٢.٢٨ سم^٣ $\ne$ ١٨٠ سم^٣ إذن التقدير خاطئ.

٢٥- تبرير: ما طول ضلع القاعدة المربعة لمنشور رباعي حجمه ١٦ متراً مكعباً وارتفاعه ٤ ‌أمتار؟

ق = ح ÷ ع.

= ١٦ ÷ ٤

= ٤ م^٢

ق = ل ع.

= ٤ م^٢

= ٢ × ٢ م٢

إذن طول ضلع القاعدة المربعة = ٢ م.

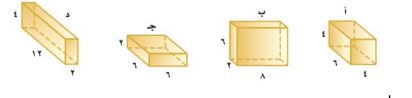
٢٦- حدد المنشور الذي لا ينتمي إلى المنشورات الأخرى فيما يأتي:

المنشور جـ حيث أن حجمه = ٧٢ وحدة مكعبة أما الباقي حجم كل منهم = ٩٦ وحدة مكعبة.

٢٧- مسألة مفتوحة: ارسم منشوراً يتراوح حجمه بين ٢٠٠ - ٤٠٠ سم^٣ وسمه ثم أعط مثالاً على مجسم له هذا الحجم التقريبي من واقع الحياة.

حجم المنشور = ل ض ع.

= ١٥ × ٥ × ٣ = ٢٢٥سم^٣

مثال على مجسم له هذا الحجم التقريبي هو علبة مجوهرات.

٢٨- اختر طريقة: لدى خديجة حوض سمك طوله ٠,٩١ م وعرضه ٠,٣٣ م وارتفاعه ٠,٤٠ م فأي الطرق الآتية أنسب كي تستعملها لتحديد عدد لترات الماء التي تحتاج إليها لملء الحوض؟

الآلة الحاسبة لأنها ضرورية لتحويل الأمتار إلى سنتمترات.

٢٩- تحد: إذا ضوعفت جميع أبعاد المنشور المقابل مرتين فهل يتضاعف حجم المنشور مرتين أيضاً؟ فسر استنتاجك.

لا تفسير الاستنتاج:

طول المنشور الموجود = عرضه = ارتفاعه = = ٣ وحدات.

إذن الحجم = ل ض ع = ٣ × ٣ × ٣ = ٢٧ وحدة مكعبة.

إذا تضاعفت الأبعاد يصبح الطول = العرض = الارتفاع = ٦ وحدات.

إذن الحجم = ٦ × ٦ × ٦ = ٢١٦ وحدة مكعبة.

أي يتضاعف الحجم ٨ مرات.

٣٠- اكتب: لماذا تستعمل الوحدات المكعبة لقياس الحجم بدلاً من استعمال الوحدات الطولية أو الوحدات المربعة؟

بما أن كل بعد من الأبعاد الثلاثة التي يتم ضربها يعبر عنه بوحدة قياس فإن الحجم يعبر عنه بوحدة قياس مكعبة وكما يعبر عن ناتج الضرب ٥ × ٥ × ٥ بالأسس عن الصورة ٥ ^٣ يعبر أيضاً عن سم × سم × سم بالأسس على الصورة سم^٣

٣١- يمكن استعمال الصندوق أدناه لوضع الأحذية فيه.

فما حجم هذا الصندوق؟

أ. ١٥٠٠٠ سم^٣

ب. ١٦٠٠٠ سم^٣

جـ. ١٨٠٠٠ سم^٣

د. ٢٠٠٠٠ سم^٣

٣٢- توضع بعض قطع الحلوى في عبوات على شكل منشور رباعي إذا كان عرض العبوة ٢٧ سم وارتفاعها ٧ سم وحجمها ٦٤٢٦ سم^٣ فما طولها؟

أ. ٣٤ سم.

ب. ٣٨ سم.

جـ. ٤٢سم.

د. ٤٦ سم.