حل أسئلة تدرب وحل المسائل

أوجد مساحة سطح كل منشور فيما يأتي:

٥-

س = ٢ ل ض + ٢ ل ع + ٢ ض ع مساحة سطح المنشور.

= ٢ (٥) (٤) + ٢ (٥) (١٢) + ٢ (٤) (١٢)

= ١٠ (٤) + ١٠ (١٢) + ٨ (١٢)

= ٤٠ + ١٢٠ + ٩٦

= ٢٥٦ ملم^٢

٦-

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (٧) (٥) + ٢(٧) (٣) + ٢(٥) (٣)

= ١٤ (٥) + ١٤ (٣) + ١٠ (٣)

= ١٤٢ سم^٢

٧-

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ ($\frac{\mathrm{٣}}{\mathrm{٤}}\mathrm{١٢}$) ($\frac{\mathrm{١}}{\mathrm{٨}}\mathrm{٨}$) + ٢($\frac{\mathrm{٣}}{\mathrm{٤}}\mathrm{١٢}$) ($\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{٤}$) + ٢($\frac{\mathrm{١}}{\mathrm{٨}}\mathrm{٨}$) ($\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{٤}$)

= ٢٥,٥ (٨,١٢٥) + ٢٥,٥ (٤,٢٥) + ١٦,٢٥ (٤,٢٥)

= ٢٠٧,١٨٧٥ + ١٠٨,٣٧٥ + ٦٩,٠٦٢٥ = $\frac{\mathrm{٣٠٧٧}}{\mathrm{٨} }=\frac{\mathrm{٥}}{\mathrm{٨}}\mathrm{٣٨٤}$ م^٢

٨-

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (٣٠) (٢٤) + ٢ (٣٠) (٢٠) + ٢ (٢٤) (٢٠)

= ٦٠ (٢٤) + ٦٠ (٢٠) + ٤٨ (٢٠)

= ١٤٤٠ + ١٢٠٠ + ٩٦٠

= ٣٦٠٠ سم^٢

٩-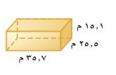

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (٣٥,٧) (٢٥,٥) + ٢ (٣٥.٧) (١٥,١) + ٢ (٢٥,٥) (١٥,١)

= ٧١,٤ (٢٥,٥) + ٧١,٤ (١٥,١) + ٥١ (١٥,١)

= ١٨٢٠,٧ + ١٠٧٨,١٤ + ٧٧٠,١

= ٣٦٦٨,٩٤ م^٢

١٠-

س = ٢ ل ض + ٢ ل ع + ض ع

= ٢ (١٠٥) (٢٥) + ٢ (١٠٥) (٢٥) + ٢٠٢٥) (٢٥)

= ٢١٠ (٢٥) + ٢١٠ (٢٥) + ٥٠ (٢٥)

= ٥٢٥٠ + ٥٢٥٠ + ١٢٥٠

١١٧٥٠ ملم^٢

١ ١- معروضات: يضع سلطان اللعبة داخل صندوق بلاستيكي شفاف كما في الشكل المجاور أوجد مساحة سطح هذا الصندوق.

س = ٢ ل ض + ٢ ل ع + 2 ض ع

= ٢ (٢٥) (١٥) ٢(٢٥) (١٠) + ٢(١٥) (١٠)

= ٥٠ (١٥) + ٥٠ (١٠) + ٣٠ (١٠)

= ٧٥٠ + ٥٠٠ + ٣٠٠

= ١٥٥٠ سم^٢

١٢- مجوهرات: تحتفظ سام ية بمجوهراتها في علبة على شكل متوازي مستطيلات طولها ١٨ سم وعرضها ١٥سم وارتفاعها ١٢ سم أوجد مساحة سطح هذه العلبة.

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (١٨) (١٥) + ٢ (١٨) (١٢) + ٢ (١٥) (١٢)

= ٣٠ (١٨) + ٢٤ (١٨) + ٣٠ (١٢)

= ٥٤٠ + ٤٣٢ + ٣٦٠

= ١٣٣٢ سم^٢

١٣- تقدير: قدرت هدى مساحة سطح منشور رباعي طوله ١٣,٢ سم وعرضه ٦م وارتفاعه ٨ م بـ ٤٦٠ م٢ فهل تقديرها معقول؟ فسر استنتاجك.

نعم تقديرها معقول.

تفسير الاستنتاج:

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (١٣,٢) (٦) + ٢ (١٣,٢) (٨) + ٢ (٦) (٨)

= ٢٤,٤ (٦) + ٢٦,٤ (٨) + ١٢ (٨)

= ١٥٨,٤ + ٢١١,٢ + ٩٦

= ٤٦٥,٦ م^٢

≈ ٤٦٠ م^٢

صنف كل قياس فيما يأتي إلى طول أو مساحة أو مساحة سطح أو حجم ثم فسر إجابتك واقترح وحدة مناسبة للقياس:

١٤- كمية الماء في بحيرة.

حجم السعة هي كمية الماء في البحيرة لتر.

١٥- مقدار الأرض التي يتطلبها بناء بيت.

مساحة حيث أن الأرض لها طول وعرض وحدة القياس المناسبة هي م^٢

١٦- مقدار الورق اللازم لتغطية صندوق.

مساحة سطح لأنه يجب معرفة جميع أبعاد الصندوق من جميع الجوانب وحدة القياس المناسبة هي سم^٢

١٧- ارتفاع شجرة.

طول لأننا نريد معرفة الارتفاع فقط وحدة القياس المناسبة هي المتر.

١ ٨- مقدار الورق اللازم لتغطية شطيرة.

مساحة سطح مجموع مساحات أوجه الشطيرة يحدد مقدار الورق اللازم لتغطيتها وحدة القياس المناسبة هي سم^٢

١٩- كمية الرمل الموجودة في صندوق.

حجم السعة هي كمية الرمل داخل الصندوق وحدة القياس المناسبة هي سم^٣

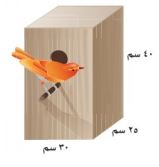
طيور: استعمل المعلومات الآتية للإجابة عن الأسئلة ٢٠ - ٢٢:

الشكل المجاور يمثل عش عصفور صنع على شكل صندوق.

٢٠- أوجد مساحة سطح صندوق العش.

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (٣٠) (٢٥) + ٢ (٣٠) (٤٠) + ٢ (٢٥) (٤٠)

= ٦٠ (٢٥) + ٦٠ (٤٠) + ٥٠ (٤٠)

= ١٥٠٠ + ٢٤٠٠ + ٢٠٠٠

= ٥٩٠٠ سم^٢

٢١- إذا زاد ارتفاع الصندوق إلى مثلي الارتفاع الأول فكم تصبح مساحة سطحه؟

ع = ٢ × ٤٠ = ٨٠ سم

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= ٢ (٣٠) (٢٥) + ٢ (٣٠) (٨٠) + ٢ (٢٥) (٨٠)

= ٦٠ (٢٥) + ٦٠ (٨٠) + ٥٠ (٨٠)

= ١٥٠٠ + ٤٨٠٠ + ٤٠٠٠

= ١٠٣٠٠ سم^٢

٢٢- إذا نقص ارتفاع الصندوق إلى النصف فكم تصبح مساحة سطحه؟

ع = ٤٠ ÷ ٢ = ٢٠ سم

س = ٢ ل ض + ٢ ل ع + ٢ ض ع مساحة سطح صندوق العش.

= ٢ (٣٠) (٢٥) + ٢ (٣٠) (٢٠) + ٢ (٢٥) (٢٠)

= ٦٠ (٢٥) + ٦٠ (٢٠) + ٥٠ (٢٠)

= ١٥٠٠ + ١٢٠٠ + ١٠٠٠

= ٣٧٠٠ سم^٢

٢٣- شحن: الشكل الآتي يمثل نوعين للطرود البريدية فأيهما مساحة سطحها أكبر؟ وهل النوع الذي مساحة أكبر هو الأكبر حجماً؟ فسر إجابتك.

النوع (١) مساحة سطحه أكبر.

تفسير الإجابة:

س = ٢ ل ض + ٢ ل ع + ٢ ض ع مساحة سطح النوع (١)

= ٢ (٣٥) (٨) + ٢ (٣٥) (٣٠) + ٢ (٨) (٣٠)

= ٧٠ (٨) + ٧٠ (٣٠) + ١٦ (٣٠)

= ٥٦٠ + ٢١٠٠ + ٤٨٠

= ٣١٤٠ سم٢

س = ٢ ل ض + ٢ ل ع + ٢ ض ع مساحة سطح النوع (٢)

= ٢ (٢٨) (٢٠) + ٢ (٢٨) (١٥) + ٢ (٢٠) (١٥)

= ٥٦ (٢٠) + ٥٦ (١٥) + ٤٠ (١٥)

= ٥٦ (٢٠) + ٥٦ (١٥) + ٤٠ (١٥)

= ١١٢٠ + ٨٤٠ + ٦٠٠

= ٢٥٦٠سم^٢

لا، النوع الذي مساحة سطحه أكبر ليس هو الأكبر حجماً فالحجمان متساويان

تفسير الإجابة:

ح = ل ض ع حجم النوع (١)

= ٣٥ × ٨ × ٣٠ = ٨٤٠٠ سم^٣

ح = ل ض ع حجم النوع (٢)

= ٢٨ × ٢٠ × ١٥ = ٨٤٠٠ سم^٣

٢٤- مسألة مفتوحة: ارسم منشوراً رباعياً مساحة سطحه ٢٠٨ سم^٢ ثم حدد أبعاده.

س = ٢ ل ض + ٢ ل ع + ٢ ض ع

= (٢× ١ × ٤) + (٢× ١١ × ٤) + (٢ × ٤ × ٤)

= ٨٨ + ٨٨ + ٣٣ = ٢٠٨ سم^٢

٢٥- تبرير: حدد إن كانت الجملة الآتية صحيحة دائماً أم صحيحة أحياناً أم غير صحيحة: "إذا زادت أبعاد مكعب إلى مثليها فستزيد مساحة سطحه أربعة أمثال".

العبارة صحيحة دائماً لأن مساحة سطح المكعب = مساحة الوجه الواحد × ٦

فإذا كان طول الحرف = ٢ سم.

إذن مساحة الوجه = ٢ × ٢ = ٤ سم، مساحة سطح المكعب.

= ٤ × ٦ = ٢٤ سم^٢

وإذا كان طول الحرف = ٤ سم.

إذن مساحة الوجه = ٤ × ٤ = ١٦ سم، مساحة سطح المكعب.

= ١٦× ٦ = ٩٦ سم^٢

لذلك إذا زادت أبعاد المكعب إلى مثليها فتزداد مساحة سطحه إلى أربعة أمثال.

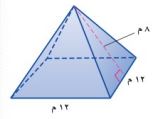
تحد: استعمل الشكل المجاور الذي جميع أوجهه المثلثية متطابقة للإجابة عن السؤالين ٢٦ - ٢٧:

٢٦- ما مساحة أحد أوجهه المثلثية؟ وما مساحة الوجه المربع منه؟

مساحة أحد أوجهه المثلثية = $\frac{\mathrm{١}}{\mathrm{٢}}$ ق ع= $\frac{\mathrm{١}}{\mathrm{٢}}$ (١٢) (٨)

= $\frac{\mathrm{١}}{\mathrm{٢}}$ (٩٦) = ٤٨ م^٢

مساحة الوجه المربع منه = طول الضلع × نفسه.

= ١٢ × ١٢ = ١٤٤ م^٢

٢٧- استعمل معلوماتك حول مساحة سطح المنشور الرباعي لتجد مساحة سطح الهرم الرباعي.

مساحة الهرم الرباعي = (٤ × مساحة أحد أوجهه المثلثية) + (مساحة الوجه المربع منه).

= (٤ × ٤٨) + (١٤٤) = ٣٣٦ م^٢

٢٨- اكتب: مسألة من واقع الحياة تحتاج في حلها إلى إيجاد مساحة سطح منشور رباعي.

وضعت زجاجة على شكل منشور رباعي داخل صندوق طوله ١٥ سم وعرضه ١٢ سم وارتفاعه ١٠ سم أوجد مساحة سطح الصندوق.

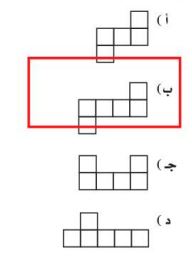
٢٩- أي مخطط مما يأتي يمثل مساحة سطح مكعب؟

٣٠- يريد مشعل عمل صندوق أبعاده ٢٣ سم ١٠ سم ٨سم أوجد مساحة سطح هذا الصندوق.

أ. ٢٤٦ سم٢

ب. ٨٢٨ سم^٢

جـ. ٩٨٨ سم^٢

د. ١٨٤٠ سم^٢