اختبار الفصل الثالث
بسط كلاً مما يأتي:
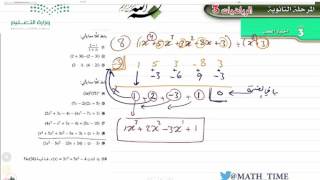
1)
2)
3)
بسط كلاً مما يأتي:
4)
5)
6)
7)
8)
9)
10) إذا كانت فما قيمة 4c(3b)؟
حلل كل كثيرة حدود فيما يأتي وإذا لم يكن ذلك ممكناً فاكتب كثيرة حدود أولية:
11)
12)
كثيرة حدود أولية
13)
حل كلاً من المعادلات الآتية:
14)
15)
16) حل المعادلة الآتية باستعمال القانون العام.
1 , 3
17) إطارات: إذا كانت مساحة الصورة وإطارها في الشكل الآتي 168 فما عرض الإطار؟
عرض الإطار 2in.
18) اختيار من متعدد: إذا كان فما قيمة f(-2)؟
الاختيار الصحيح B.
19) فيما يأتي كثيرة حدود وأحد عواملها أوجد عواملها الأخرى:
اذكر العدد الممكن للأصفار الحقيقية الموجبة والحقيقية السالبة والتخيلية لكل من الدالتين الآتيتين:
20)
2,1 أو 2 ,0 أو 0
21)
1 , 1 ,4
أوجد جميع أصفار كل من الدالتين الآتيتين:
22)
23)
24) هندسة: إذا كان حجم المنشور المتوازي المستطيلات َالموضح بالشكل أدناه 612 فأوجد أبعاده.
9cm , 14 cm , 4cm
25) صف سلوك طرفي التمثيل البياني الآتي وحدد ما إذا كانت درجة دالة كثيرة الحدود فردية أم زوجية واذكر عدد الأصفار الحقيقية للدالة.
مشاركة الدرس
الاختبارات
اختبار الكتروني: اختبار الفصل الثالث
100%
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]%;" role="progressbar" aria-valuenow="
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">

.JPG)
.JPG)
.JPG)


النقاشات