تدرب وحل المسائل
أوجد مجموع قياسات الزوايا الداخلية لكل من المضلعات المحدبة الآتية:
12) ذو 12 ضلعاً.
الحل:
n=12
(n-2).180 = (12-2).180 =1800
13) ذو 20 ضلعاً.
الحل:
n=20
(n-2).180 = (20-2).180 =3240
14) ذو 29 ضلعاً.
الحل:
n=29
(n-2).180 = (12-2).180 =4860
15) ذو 32 ضلعاً.
n=32
(n-2).180 = (12-2).180 =4500
أوجد قياسات جميع الزوايا الداخلية لكل من المضلعات الآتية:
16)
الحل:
بما ان الشكل رباعي اذن مجموع قياسات الزوايا الداخلية له =
(n-2).180 = (4-2).180 =360
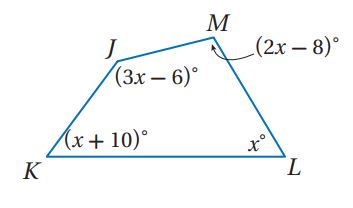
17)
الحل:
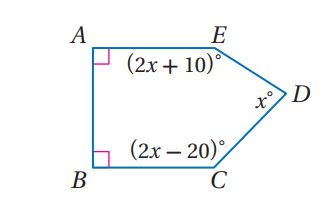
18)
الحل:
بما أن الشكل خماسي إذن مجموع قياسات الزوايا الداخلية له =
19)
الحل:
بما أن الشكل خماسي إذن مجموع قياسات الزوايا الداخلية له =
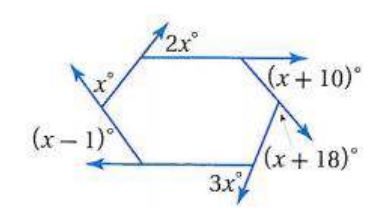
20) ما مجموع قياسات الزوايا الداخلية للمضلع في الشكل المجاور؟
الحل:
n=5
(n-2).180 = (5-2).180 =540
أوجد قياس زاوية داخلية لكل من المضلعات المنتظمة الآتية:
21) ذو 12 ضلعاً.
الحل:
n=12
(n-2).180 = (12-2).180 =1800
22) الخماسي.
الحل:
n=12
(n-2).180 = (5-2).180 =540
23) العشاري.
الحل:
n=12
(n-2).180 = (10-2).180 =1440
24) التساعي.
الحل:
n=12
(n-2).180 = (9-2).180 =1260
إذا كان قياس إحدى الزوايا الداخلية لمضلع منتظم معطى فأوجد عدد الأضلاع في كل مما يأتي:
25) 60º
الحل:
إذا كان قياس كل زاوية خارجية للمضلع المنتظم ذي 3 ضلعاً يساوي 60º.
26) 90º
الحل:
إذا كان قياس كل زاوية خارجية للمضلع المنتظم ذي 4 ضلعاً يساوي 60º.
27) 120º
الحل:
إذا كان قياس كل زاوية خارجية للمضلع المنتظم ذي 6 ضلعاً يساوي 120º.
28) 156º
الحل:
إذا كان قياس كل زاوية خارجية للمضلع المنتظم ذي 15 ضلعاً يساوي 156º.
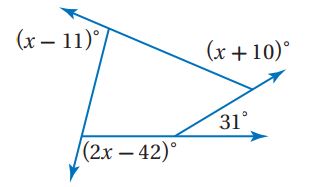
أوجد قيمة x في كل من الشكلين الآتيين:
29)
الحل:
30)
الحل:
أوجد قياس زاوية خارجية لكل من المضلعات المنتظمة الآتية:
31) العشاري.
الحل:
نظرية مجموع الزوايا الخارجية لمضلع.
32) الخماسي.
الحل:
نظرية مجموع الزوايا الخارجية لمضلع.
33) السداسي.
الحل:
نظرية مجموع الزوايا الخارجية لمضلع.
34) ذو 15 ضلعاً.
الحل:
نظرية مجموع الزوايا الخارجية لمضلع.
35) تصوير: تشكل الفتحة التي ينفذ منها الضوء إلى عدسة آلة التصوير في الشكل المجاور مضلعاً منتظماً ذا 14 ضلعاً.
a) أوجد قياس الزاوية الداخلية مقرّبة إلى أقرب عُشر.
الحل:
2160=180. (14-2) n=14
قياس الزاوية الداخلية = = 154.3 تقريباً.
b) أوجد قياس الزاوية الخارجية مقرّبة إلى أقرب عُشر.
الحل:
360 = 14n (نظرية مجموع قياسات الزوايا الخارجية للمضلع).
25.7=n (بقسمة كلا الطرفين على 14).
اذن قياس الزاوية الداخلية = 154.3 تقريباً.
أوجد قياس زاوية خارجية وزاوية داخلية للمضلع المنتظم المعطى عدد أضالعه في كل مما يأتي وقرب إجابتك الى أقرب عشرة:
36) 7
الحل:
900=180. (7-2) n=7
قياس الزاوية الداخلية = = 128.6 تقريباً.
360 = 7n (نظرية مجموع قياسات الزوايا الخارجية للمضلع).
51.4=n (بقسمة كلا الطرفين على7).
إذن قياس الزاوية الداخلية = 51.4 تقريباً.
37) 13
الحل:
1980=180. (13-2) n=13
قياس الزاوية الداخلية = = 152.3 تقريباً.
360 = 13n (نظرية مجموع قياسات الزوايا الخارجية للمضلع).
51.4=n (بقسمة كلا الطرفين على13).
إذن قياس الزاوية الداخلية = 27.7 تقريباً.
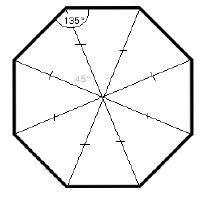
38) أثبت أن مجموع قياسات الزوايا الداخلية للمضلع الثماني يساوي °1080، دون استعمال صيغة مجموع الزوايا الداخلية للمضلع.
الحل:
يقسم المضلع إلى ثمان مثلثات.
مجموع زوايا 8 مثلثات = 8 × 180
= 1440
مجموع الزوايا حول نقطة المركز = 360
مجموع زويا المضلع الثماني الداخلية = 1440 - 360 = 1080
قياس الزاوية الداخلية للمضلع الثماني المنتظم = 1080 ÷ 8 = 135
39) برهان: استعمل الجبر لإثبات نظرية مجموع قياسات الزوايا الخارجية للمضلع.
الحل:
أفرض أن N تساوي مجموع قياسات الزوايا الخارجية لمضلع عدد أضلاعه n.
N تساوي مجموع قياسات الأزواج الخطية مطروحاً منه مجموع قياسات الزوايا الداخلية.
=180n - 180 (n-2)
=180n - 180n + 360 = 360
لذا، فإن مجموع قياسات الزوايا الخارجية لأي مضلع محدب يساوي 360
جبر: أوجد قياسات جميع الزوايا الداخلية لكل من المضلعين الآتيين:
40) عشاري قياسات زواياه الداخلية:
(x+5)º,(x+10)º,(x+20)º,(x+30)º,(x+35)º,(x+40)º,(x+60)º,(x+70)º,(x+80)º,(x+90)º
الحل:
41) الخماسي ABCDE الذي قياسات زواياه الداخلية:
6xº,(4x + 13)º , (x + 9)º , (2x - 8)º ,(4x - 1)
الحل:
42) تمثيلات متعددة: سوف تستقصي في هذه المسألة العالقات بين الزوايا والأضالع في متوازي أضلاع.
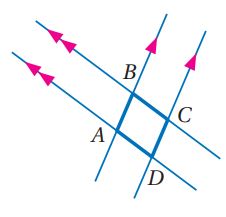
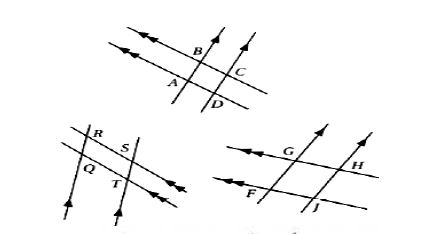
a) هندسياً: رسم زوجين من المستقيمات المتوازية تتقاطع كما في الشكل المجاور، وسم الشكل الرباعي الناتج ABCD ثم كرر هذه الخطوات لتكوين شكلين آخرين: QRST,FGHJ.
الحل:
b) جدولياً: أكمل الجدول الآتي:
الحل:
| الشكل الرباعي | أطوال الأضلاع وقياسات الزوايا | |||||||
| ABCD | 101 | 97 | 101 | 97 | ||||
| AB | 0.6cm | BC | 0.6cm | CD | 0.6cm | DA | 0.6cm | |
| FGHJ | 76 | 104 | 76 | 104 | ||||
| FG | 1cm | GH | 0.9cm | HJ | 1cm | JF | 0.9cm | |
| QRST | 121 | 95 | 121 | 95 | ||||
| QR | 0.5cm | RS | 1.2cm | ST | 0.5cm | TQ | 1.2cm | |
c) لفظياً: خمن العلاقة بين كل زاويتين متقابلتين في الشكل الرباعي الناتج عن زوجين من المستقيمات المتوازية.
الحل:
في الشكل الرباعي المتكون من زوجين من المستقيمات المتوازية تكون الزاويتان المتقابلتان متطابقتين.
d) لفظياً: خمن العلاقة بين كل زاويتين متخالفتين في الشكل الرباعي الناتج عن زوجين من المستقيمات المتوازية.
الحل:
في الشكل الرباعي المتكون من زوجين من المستقيمات المتوازية تكون الزاويتان المتخالفتان متكاملتين.
e) لفظياً: خمن العلاقة بين كل ضلعين متقابلين في الشكل الرباعي الناتج عن زوجين من المستقيمات المتوازية.
الحل:
في الشكل الرباعي المتكون من زوجين من المستقيمات المتوازية تكون الضلعان المتقابلتان متطابقتين.



.JPG)
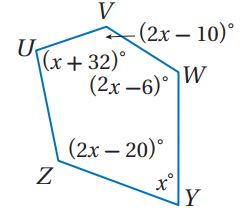











النقاشات