تأكد

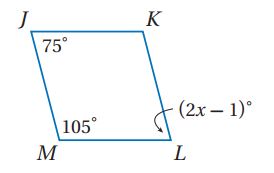
1) ملاحة: يستعمل البحارة مسطرتين متوازيتين يصل بينهما ذراعان متساويا الطول لتحديد اتجاه إبحارهم فيضعون إحدى المسطرتين بمحاذاة مسار الإبحار ثم يحركون المسطرة الأخرى حتى تصل إلى قرص بوصلة مرسومة على الخريطة تشكل المسطرتان والذراعان الواصلتان بينهما MNPQ.

a) إذا كان MQ =2in، فأوجد NP.

الحل:

NP=2in لأن كل ضلعين متناظرين متطابقين.

b) إذا كان $m\angle NMQ = 38°$ فأوجد $m\angle MNP$.

الحل:

كل زاويتين متحالفتين مجموعهم = 180º.

$\begin{array}{l}38+\mathrm{m}\mathrm{\angle }\mathrm{NMQ}={180}^{\circ }\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{NMQ}=180-38\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{NMQ}={142}^{\circ }\end{array}$

C) إذا كان $m\angle MQP = 128°$ فأوجد $m\angle MNP$.

الحل:

من خصائص متوازي الأضلاع كل زاويتين متقابلتين متطابقتين.

$\angle MNP = 128°$

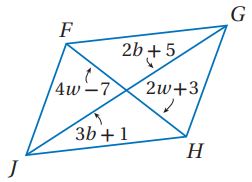
جبر: أوجد قيمة المتغير في كل من متوازيي الأضلاع الآتيين:

2) الحل: من خصائص متوازي الأضلاع كل زاويتين متقابلتين متطابقتين.

$\begin{array}{l}\mathrm{\angle }\mathrm{L}={75}^{\circ }\\ \\ 2\mathrm{x}-1=75\\ \\ 2\mathrm{x}=76\\ \\ \mathrm{x}=38\end{array}$

3) الحل: حسب نظرية قطرا متوازي الأضلاع.

$\begin{array}{l}2w+3=4w-7\\ \\ 2w-4w=-7-3\\ \\ -2w=-10\\ \\ w=5\\ \\ 2b+5=3b+1\\ \\ 2b-3b=1-5\\ \\ -b=-4\\ \\ b=4\end{array}$

4) هندسة احداثية: أوجد إحداثيي نقطة تقاطع قطري ABCD الذي رؤوسه $A(-4,6),B(5,6),C(4,-2),D(-5,-2)$.

الحل:

بما أن قطري متوازي الأضلاع ينصف كل منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من $\cdot \overline{\mathrm{AC}},\overline{\mathrm{BD}}$ أوجد نقطة منتصف $\overline{\mathrm{AC}}$ التي طرفاها $(-4\cdot 6),(4-2)$.

$\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)=\left(\frac{-4+4}{2},\frac{6-2}{2}\right)$ (صيغة نقطة المنتصف).

$\begin{array}{l}\mathrm{m}\mathrm{\angle }\mathrm{WZX}+\mathrm{m}\mathrm{\angle }\mathrm{ZXW}={90}^{\circ }\\ \\ \mathrm{x}-11+\mathrm{x}-9=90\\ \\ 2\mathrm{x}-20=90\\ \\ 2\mathrm{x}=110\\ \\ \mathrm{x}=55\\ \\ \mathrm{\angle }\mathrm{ZXW}=\mathrm{x}-11=55-11\\ \\ \mathrm{\angle }\mathrm{ZXW}=44\\ \\ \mathrm{\angle }\mathrm{ZXY}=90-44={46}^{\circ }\end{array}$

(بالتبسيط)

إذن إحداثياً نقطة تقاطع قطري $\overline{ABCD}$ هم (0,2)

برهان: اكتب برهاناً من النوع المحدد في كل من السؤالين الآتيين:

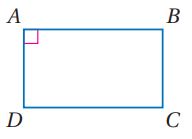
5) برهانا حراً.

المعطيات: ABCD متوازي أضلاع $\angle A$ قائمة.

المطلوب: $\angle B,\angle C,\angle D$ قوائم (النظرية 1.6).

الحل:

• المعطيات: ABCD متوازي اضلاع فيه الزاوية A قائمة
• المطلوب: الزوايا B,C,D قوائم (النظرية 5.6)
• البرهان: حسب تعريف متوازي الأضلاع $\overline{\mathrm{AD}}\parallel \overline{\mathrm{CB}}$ ولأن $\angle A$ قائمة فإن $\overline{\mathrm{AD}}\perp \overline{\mathrm{AB}}$ وحسب نظرية القاطع العمودي يكون $\overline{\mathrm{AB}}\perp \overline{\mathrm{CB}}$ إذن $\angle B$قائمة لأن المستقيمين المتعامدين يشكلان زاوية قائمة وكذلك $\mathrm{\angle }\mathrm{A}\cong \mathrm{\angle }\mathrm{C},\mathrm{\angle }\mathrm{D}\cong \mathrm{\angle }\mathrm{B}$ لأن الزوايا المتقابلة في متوازي الأضلاع متطابقة إذن الزوايا C، D قائمتان لأن لجميع الزوايا المتطابقة القياس نفسه.

6) برهاناً ذا عمودين.

المعطيات: ABCH,DCGF متوازي أضلاع.

المطلوب: $\angle A \cong \angle F$

الحل:

• المعطيات: متوازي الأضلاع DCGF,ABCH
• المطلوب: $\mathrm{\angle }\mathrm{A}\cong \mathrm{\angle }\mathrm{F}$

البرهان:

العبارات (المبررات):

1) ABCH وDCGF متوازي أضلاع (معطى).

2) $\widehat{\text{ E }}\mathrm{DCG}\cong \widehat{\text{ E}} \mathrm{BCH}$ (الزاويتان المتقابلتان بالأس متطابقتان).

3) $\ddot{E}\mathrm{DCG}\cong \ddot{E}\mathrm{F},\ddot{E}\mathrm{BCH}\cong \text{ EA }$ (الزوايا المتقابلة في متوازي الأضلاع متطابقة).

4) $\ddot{\mathrm{E}}\mathrm{F}\cong \ddot{E}A$ (خاصية التعدي).