مراجعة تراكمية
هندسة إحداثيات: أوجد نقطة تقاطع قطري متوازي الأضلاع ABCD في كل من السؤالين الآتيين: (الدرس 2-1).
43)
الحل:
بما أن قطرا متوازي الأضلاع ينصف كل منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من أوجد نقطة منتصف التي طرفاها (4- ,5) ,(5 ,3-).
(صيغة نقطة المنتصف).
(0.5 , 1) (بالتبسيط)
إذن إحداثياً نقطة تقاطع قطري RSTU هما (0.5 , 1).
44)
الحل:
بما أن قطرا متوازي الأضلاع ينصف كل منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من أوجد نقطة منتصف التي طرفاها (2- ,7)، (5 , 2).
(صيغة نقطة المنتصف).
(1.5 , 4.5) (بالتبسيط).
إذن إحداثياً نقطة تقاطع قطري RSTU هما (1.5 , 4.5).
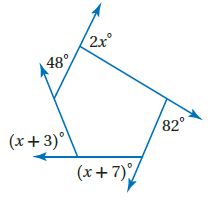
أوجد قيمة x في كل من الأسئلة الآتية: (الدرس 1-1).
45)
الحل:
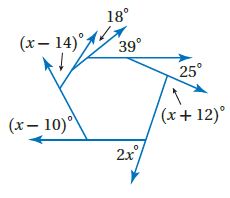
46)
الحل:
47)
الحل:
أوجد عدد أضلاع المضلع المنتظم المعطى قياس إحدى زواياه الداخلية في كل مما يأتي: (الدرس 1-1).
48) 140º
الحل:
49) 160º
الحل:
50) 168º
الحل:
51) 162º
الحل:
استعمل الميل لتحديد ما إذا كان متعامدتين أم لا في كل مما يأتي:
52)
الحل:
غير متعامدين لأن حاصل ضرب ميل كل منهما لا يساوي 1-
53)
الحل:
غير متعامدتين لأن حاصل ضرب ميل كل منهما لا يساوي 1-

.JPG)
.jpg)
.JPG)
.JPG)



النقاشات