تدرب وحل المسائل

أوجد القياس المطلوب في كل من السؤالين الآتيين:

8) $m\angle K$

الحل:

بما أن $KL = JM و JK\parallel ML$ إذن الشكل شبه منحرف متطابق الضلعين وبالتالي يكون زوايا القاعدة متساوية.

$$\begin{gathered} \angle J = 180 - 80 = 100 \\ m\angle J = m\angle K =100° \end{gathered}$$ نظرية الزوايا المتحالفة.

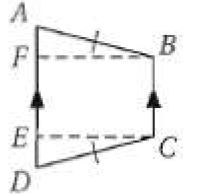
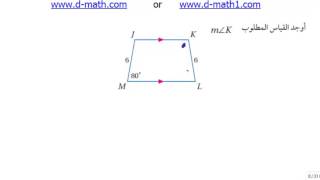
9) PW إذا كان: ZX = 20, TY = 15

الحل:

بما أن $XW = YZ و WZ\parallel XY$ إذن الشكل شبه منحرف متطابق الضلعين ويكون قطراه متطابقان.

$\begin{array}{l}\mathrm{XZ}=\mathrm{WY}\\ \\ 18=\mathrm{YP}+\mathrm{PW}\\ \\ 18=3+\mathrm{PW}\\ \\ \mathrm{PW}=18-3=15\end{array}$

هندسة إحداثية: بين أن الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي شبه منحرف وحدد ما إذا كان متطابق الساقين؟

10) A(-2,5), B(-3,1), C(6,1), D(3,5)

الحل:

الخطوة 1:

$\begin{array}{r}\frac{1}{4}=\frac{-2+3}{5-1}=\overline{\mathrm{AB}} \mathrm{ميل}\\ \\ \frac{3}{-4}=\frac{6-3}{1-5}=\overline{\mathrm{CD}} \mathrm{ميل}\end{array}$

بما أن ميل كل من$\overline{CD},\overline{AB}$ليس متساويان إذن $\overline{AB}\nparallel \overline{CD}$

$\begin{array}{r}0=\frac{0}{9}=\frac{1-1}{-3-6}=\overline{BC} \mathrm{ميل}\\ \\ 0=\frac{0}{5}=\frac{5-5}{3+2}=\overline{AD} \mathrm{ميل}\end{array}$

بما أن ميل كل من$\overline{AD},\overline{BC}$ متساويان إذن $\overline{AD}\parallel \overline{BC}$ وبما أن ABCD فيه ضلعان فقط متوازيان فهو شبه منحرف.

الخطوة 2:

$\begin{array}{r}\overline{\mathrm{AB}}=\sqrt{(-2+3{)}^2+(5-1{)}^2}=\sqrt{17}\\ \\ \overline{\mathrm{CD}}=\sqrt{(6-3{)}^2+(1-5{)}^2}=\sqrt{25}=5\end{array}$

ABCD هو شبه منحرف ولكن ليس متطابق الساقين لأن:

$AB = \sqrt{17},CD=5$

11) J(-4,-6), K(6,2), L(1,3), M(-4,-1)

الحل:

الخطوة 1:

$\begin{array}{r}\frac{5}{4}=\frac{-10}{-8}=\frac{-4-6}{-6-2}=\overline{JK} \mathrm{ميل}\\ \\ \frac{5}{4}=\frac{1+4}{3+1}=\overline{ML} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{ML},\overline{JK}$ متساويان إذن $\overline{ML}\parallel \overline{JK}$

$\begin{array}{r}-5=\frac{5}{-1}=\frac{6-1}{2-3}=\overline{KL} \mathrm{ميل}\\ \\ \frac{0}{-5}=\frac{-4+4}{-6+1}=\overline{JM} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{JM},\overline{KL}$ ليس متساويان إذن $\overline{JM}\nparallel \overline{KL}$ وبما إن $JKLM$ فيه ضلعان فقط متوازيان وهما فهو شبه منحرف.

الخطوة 2:

$\begin{array}{r}\overline{\mathrm{KL}}=\sqrt{(6-1{)}^2+(2-3{)}^2}=\sqrt{26}\\ \\ \overline{\mathrm{JM}}=\sqrt{(-4+4{)}^2+(-6+1{)}^2}=\sqrt{25}=5\end{array}$

JKLM هو شبه منحرف ولكن ليس متطابق الساقين؛ لأن

$.KL=\sqrt{26},JM=5$

12) Q(2,5), R(-2,1), S(-1,-6), T(9,4)

الحل:

الخطوة 1:

$\begin{array}{r}1=\frac{4}{4}=\frac{2+2}{5-1}=\overline{QR} \mathrm{ميل}\\ \\ 1=\frac{10}{10}=\frac{-1-9}{-6-4}=\overline{ST} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{ST},\overline{QR}$ متساويان إذن$\overline{ST}\parallel \overline{QR}$

$\begin{array}{r}\frac{-1}{7}=\frac{-2+1}{1+6}=\overline{RS} \mathrm{ميل}\\ \\ -7=\frac{-7}{1}=\frac{2-9}{5-4}=\overline{QT} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{QT},\overline{RS}$ ليس متساويان إذن $\overline{QT}\nparallel \overline{RS}$ وبما أن QRST فيه ضلعان فقط متوازيان فهو شبه منحرف.

الخطوة 2:

$\begin{array}{r}\overline{\mathrm{RS}}=\sqrt{(-2+1{)}^2+(1+6{)}^2}=\sqrt{50}\\ \\ \overline{\mathrm{QT}}=\sqrt{(2-9{)}^2+(5-4{)}^2}=\sqrt{50}\end{array}$

بما أن $\overline{QT}=\overline{RS}$ فإن شبه المنحرف QRST متطابق الساقين QRST هو شبه منحرف متطابق الساقين.

13) W(-5,-1), X(-2,2), Y(3,1), Z(5,-3)

الحل:

$\begin{array}{r}1=\frac{-3}{-3}=\frac{-5+2}{-1-2}=\overline{WX} \mathrm{ميل}\\ \\ \frac{-1}{2}=\frac{-2}{4}=\frac{3-5}{1+3}=\overline{YZ} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{WX},\overline{YZ}$ ليس متساويان إذن $\overline{WX}\nparallel \overline{YZ}$

$\begin{array}{r}-5=\frac{-5}{1}=\frac{-2-3}{2-1}=\overline{XY} \mathrm{ميل}\\ \\ -5=\frac{-10}{2}=\frac{-5-5}{-1+3}=\overline{WZ} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{WZ},\overline{XY}$ متساويان إذن $\overline{WZ}\parallel \overline{XY}$ وبما أن XWYZ فيه ضلعان فقط متوازيان فهو شبه منحرف.

الخطوة 2:

$\begin{array}{r}\overline{WX}=\sqrt{(-5+2{)}^2+(-1-2{)}^2}=\sqrt{18}\\ \\ \overline{YZ}=\sqrt{(3-5{)}^2+(1+3{)}^2}=\sqrt{20}\end{array}$

بما أن $\overline{WX}=\overline{YZ}$ فإن شبه المنحرف WXYZ متطابق الساقين شبه منحرف لأن $YZ = \sqrt{20},WX=\sqrt{18}$.

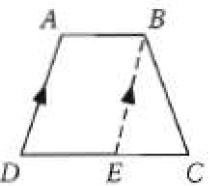
في الشكل المجاور S,V نقطتا منتصفي الساقين لشبه المنحرف QRTU.

14) إذا كان QR = 12,UT = 22 فأوجد VS

الحل:

القطعة المتوسطة لشبه المحرف =$\frac{1}{2}$ مجموع طولي القاعدة.

$\begin{array}{l}\text{ VS }=\frac{1}{2}(12+22)\\ \\ \text{ VS }=\frac{1}{2}(12+22)=17\end{array}$

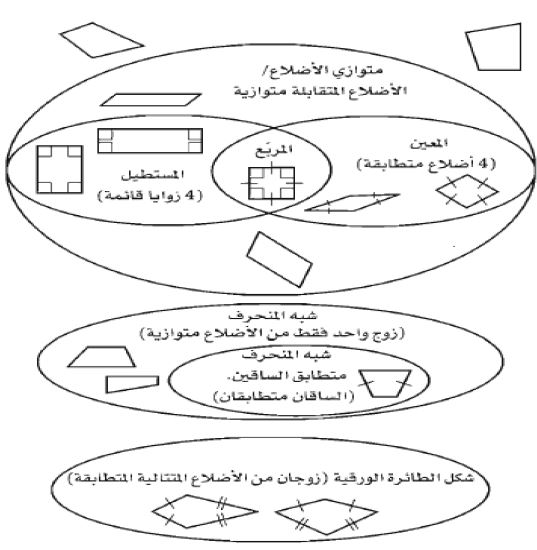
15) إذا كان VS = 9,UT = 12 فأوجد QR

الحل:

$\begin{array}{l}\mathrm{VS}=\frac{1}{2}(\mathrm{QR}+\mathrm{UT})\\ \\ 9=\frac{1}{2}(\mathrm{QR}+12)\\ \\ 18=\mathrm{QR}+12\\ \\ \mathrm{QR}=18-12\\ \\ \mathrm{QR}=6\end{array}$

16) إذا كان RQ = 5,VS = 11 فأوجد UT

الحل:

$\begin{array}{l}\mathrm{VS}=\frac{1}{2}(\mathrm{QR}+\mathrm{UT})\\ \\ 11=\frac{1}{2}(5+\mathrm{UT})\\ \\ 22=5+\mathrm{UT}\\ \\ \mathrm{UT}=22-5\\ \\ \mathrm{UT}=17\end{array}$

إذا كان WXYZ شكل طائرة ورقية فأوجد القياس المطلوب في كل مما يأتي:

17) WP

الحل:

قطرا شكل الطائرة متعامدان وباستخدام فيثاغورث ينتج أن:

$\begin{array}{l}(WX{)}^2=(XP{)}^2+(WP{)}^2\\ \\ (6{)}^2=(4{)}^2+(WP{)}^2\\ \\ (WP{)}^2=36-16\\ \\ (WP{)}^2=\sqrt{20}\end{array}$

18) $m\angle X$

الحل:

بما أن الشكل رباعي إذن مجموع زواياه الداخلية =--

وبما أن الشكل طائرة ورقية إذن $\angle X=\angle Z$

$\begin{array}{l}\mathrm{\angle }X+\mathrm{\angle }Y+\mathrm{\angle }Z+\mathrm{\angle }W={360}^{\circ }\\ \\ \mathrm{\angle }X=\mathrm{\angle }Z\\ \\ 2\mathrm{\angle }X+56+70={360}^{\circ }\\ \\ \mathrm{\angle }X={117}^{\circ }\end{array}$

برهان: اكتب برهاناً حراً لكل من النظريات الآتية:

19) النظرية 1.21

الحل:

المعطيات: ABCD شبه منحرف متطابق الساقين.

$\overline{\mathrm{BC}}\cong \overline{\mathrm{AD}},\overline{\mathrm{AB}}\cong \overline{\mathrm{CD}}$

المطلوب: $\mathrm{\angle }\mathrm{A}\cong \mathrm{\angle }\mathrm{D},\mathrm{\angle }\mathrm{ABC}\cong \mathrm{\angle }\mathrm{DCB}$

البرهان: ارسم المستقيمين $\overline{CE}و\overline{BF}$ بحيث يكون $\overline{CE}\perp \overline{AD} و \overline{BF}\perp \overline{AD}$.

وبما أن $\overline{BC}\parallel \overline{AD}$ والمسافة بين المستقيمين المتوازيين ثابتة $\overline{BF}\parallel \overline{CE}$ وبما أن المستقيمين المتعامدين يشكلان زوايا قائمة فإن $\angle CED=\angle BFA$ قائمتان.

إذن $△BFA\cong △CED$ بحسب حالة التطابق$\left(HL\right)$ وبما أن العناصر المتناظرة في مثلثين متطابقين متطابقة فإن $\angle A\cong \angle D$ وبما أن $\mathrm{\angle }\mathrm{BCE}\cong \mathrm{\angle }\mathrm{CBF}$ قائمتان وجميع الزوايا القائمة متطابقة فإن $\mathrm{\angle }\mathrm{ABF}\cong \mathrm{\angle }\mathrm{DCE} و \mathrm{\angle }\mathrm{CBF}\cong \mathrm{\angle }\mathrm{BCE}$ لأن العناصر المتناظرة في مثلثين متطابقين متطابقة.

إذا $\angle ABC \cong \angle DCB$ وفق مسلمة جمع الزوايا.

20) النظرية 1.22

الحل:

المعطيات: ABCD شبه منحرف فيه $\angle D \cong \angle C$

المطلوب: إثبات أن ABCD متطابق الساقين.

البرهان: ارسم القطعة المستقيمة المساعدة EB بحيث تكون $\overline{EB}\parallel \overline{AD}$

وبذلك تكون $\angle D\cong \angle BEC$ حسب مسلمة الزوايا المتناظرة.

ونعلم أن $\angle D\cong \angle C$ إذن وحسب خاصية التعدي تكون $\angle BEC\cong \angle C$ إذن فالمثلث $△EBC$ متطابق الضلعين , حيث $\overline{EB}\cong \overline{BC}$ ومن تعريف شبه المنحرف $\overline{AB}\parallel \overline{DE}$

وبما أن كل ضلعين متقابلين للشكل ABED متوازيان فإنه متوازي أضلاع.

$\overline{AD}\cong \overline{EB}$ وحسب خاصية التعدي يكون $\overline{BC}\cong \overline{AD}$ لذلك فشبه المنحرف ABCD متطابق الساقين.

21) النظرية 1.23

الحل:

المعطيات: ABCD شبه منحرف $\overline{AC}\cong \overline{BD}$

المطلوب: اثبات ان شبه المنحرف ABCD متطابق الساقين.

البرهان: نعلم أن ABCD شبه منحرف فيه $\overline{AC}\cong \overline{BD}$.

ارسم القطعتين المساعدتين $\overline{AE} و \overline{BF}$ بحيث تكون $\overline{BF}\perp \overline{DC} و \overline{AE}\perp \overline{DC}$ وبما أن المستقيمين المتعامدين يشكلان زوايا قائمة فإن $\angle BFEو \angle AEF$ قائمتان لذلك $△BFD و △AEC$ قائما الزاوية حسب التعريف وبما أن $\overline{AE}\cong \overline{BF}$ لأن المستقيمين اللذين يقعان في نفس المستوى والعموديين على مستقيم واحد يكونان متوازيين ,فإن $\overline{AE}\cong \overline{BF}$ لأن الأضلاع المتقابلة في متوازي الأضلاع متطابقة.

ومن ذلك يكون $△AEC\cong △BFD$ حسب حالة التطابق(HL) و $\angle ACD \cong \angle BDC$ لأن العناصر المتناظرة في مثلثين متطابقين متطابقة.

كذلك $\overline{DC}\cong \overline{DC}$ حسب خاصية الانعكاس للتطابق.

إذن $△ACD \cong △BDC$ حسب حالة التطابق (SAS) وبما أن العناصر المتناظرة في المثلثين المتطابقين متطابقة فإن $\overline{AD}\cong \overline{BC}$ لذلك شبه المنحرف ABCD متطابق الساقين.

22) النظرية 1.25

الحل:

المعطيات: ABCD شكل طائرة ورقية فيه $\overline{\mathrm{AD}}\cong \overline{\mathrm{DC}},\overline{\mathrm{AB}}\cong \overline{\mathrm{BC}}$.

المطلوب: $\overline{BD}\perp \overline{AC}$.

البرهان: تعلم أن $\overline{\mathrm{AD}}\cong \overline{\mathrm{AD}}و \overline{\mathrm{AB}}\cong \overline{\mathrm{BC}}$

إذن B وD كلاهما على بعدين متساويين من A وC.

وإذا كانت نقطة على بعدين متساويين من طرفي قطعة مستقيمة فإنها تقع على العمود المنصف لتلك القطعة.

إذن فالمستقيم الذي يحوي النقطتين B وD عمود منصف ل $\overline{AC}$ لأنه لا يوجد إلا مستقيم واحد فقط يمر في نقطتين مختلفتين.

لذلك $\overline{BD}\perp \overline{AC}$.

23) النظرية 1.26

الحل:

المعطيات: ABCD شكل طائرة ورقية

المطلوب: $\angle B \cong \angle D$

البرهان: نعلم أن $\overline{\mathrm{BC}}\cong \overline{\mathrm{CD}} و \overline{\mathrm{AB}}\cong \overline{\mathrm{AD}}$ حسب تعريف شكل الطائرة الورقية.

$\overline{AC}\cong \overline{AC}$ خاصية الانعكاس.

لذلك $△ABC \cong △ADC$ حسب (SSS).

إذن $\angle B \cong \angle D$ لأن العناصر المتناظرة في المثلثين المتطابقين متطابقة.

وإذا كان $\angle BAD \cong \angle BCD$ فإن ABCD متوازي أضلاع حسب التعريف وهو ما لا يكون صحيحاً لأننا نعلم أن ABCD شكل طائرة ورقية لذلك $\angle BAD \cong \angle BCD$

24) نباتات: اشترى مشاري أصيصاً زراعياً أوجهه الأربعة على شكل شبه منحرف أبعاده كما في الشكل المجاور إذا أراد مشاري وضع رف أفقي عند منتصف الأصيص لتستند إليه النبتة فكم يكون عرض هذا الرف؟

الحل:

بما أن الشكل شبه منحرف والقطعة المتوسطة لهذا الرف = $\frac{1}{2}$ مجموع القاعدتين.

$\frac{1}{2}(26+14)=\frac{1}{2}\left(40\right)=20$

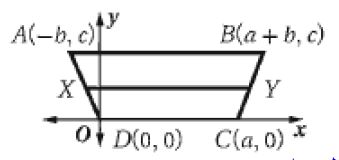
25) برهاناً: اكتب برهاناً إحداثياً للنظرية 1.24

الحل:

المعطيات: ABCD شبه منحرف فيه $\overline{XY}$ قطعة متوسطة.

المطلوب: $\overline{XY }\parallel \overline{AB},\overline{XY}\parallel \overline{DC}$

البرهان:

X نقطة منتصف $\overline{AD}$واحداثياتها $\left(\frac{-b}{2},\frac{c}{2}\right)$

Y نقطة منتصف $\overline{BC}$ وإحداثياتها $\left(\frac{2a+b}{2},\frac{c}{2}\right)$

وبما أن ميل $\overline{AB}$ يساو يصفر وميل $\overline{XY}$ يساوي صفر وميل $DC$ يساوي صفر فإن $\overline{XY}\parallel \overline{AB} , \overline{XY}\parallel \overline{DC}$.

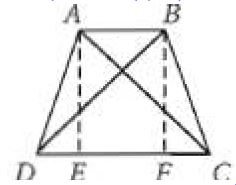
26) هندسة إحداثية: استعن بالشكل الرباعي ABCD المجاور.

a) بين أن ABCD شبه منحرف وحدد ما إذا كان متطابق الساقين. وضح إجابتك.

الحل:

الخطوة 1:

$\begin{array}{c}\frac{-4}{3}=\frac{1-5}{3-0}=\overline{BC} \text{ ميل}\\ \frac{-4}{3}=\frac{-8}{6}=\frac{-3-5}{2+4}=\overline{AD} \mathrm{ميل}\\ 0=\frac{0}{4}=\frac{5-5}{0+4}=\overline{CD} \mathrm{ميل}\\ 4=\frac{-4}{-1}=\frac{-3-1}{2-3}=\overline{AB} \mathrm{ميل}\end{array}$

بما أن ميل كل من $\overline{AD},\overline{BC}$ متساويان إذن $\overline{AD}\parallel \overline{BC}$ وميل كلا من $\overline{CD},\overline{AB}$ غير متساويان إذن $\overline{CD}\nparallel \overline{AB}$ إذن الشكل ABCD شبه منحرف.

الخطوة 2:

$\begin{array}{l}\overline{\mathrm{AB}}=\sqrt{(-3-1{)}^2+(2-3{)}^2}=\sqrt{17}\\ \\ \overline{\mathrm{CD}}=\sqrt{(5-5{)}^2+(0+4{)}^2}=\sqrt{25}=\sqrt{16}=4\end{array}$

إذن ABCD شبه منحرف ولكنه غير متطابق الساقين لأن $CD = 4 و AB = \sqrt{17}$

b) هل القطعة المتوسطة محتواة في المستقيم الذي معادلته y = -x + 1؟ برر إجابتك.

الحل:

لا؛ لأن هذا المستقيم لا يوازي قاعدتي شبه المنحرف حيث إن ميل كل من القاعدتين $\frac{-3}{4}$ على حين أن ميل المستقيم $Y=-X + 1$ يساوي 1- .

c) أوجد طول القطعة المتوسطة.

الحل:

$\begin{array}{r}\overline{\mathrm{BC}}=\sqrt{(5-1{)}^2+(3-0{)}^2}=\sqrt{25}=5\\ \\ \overline{\mathrm{AD}}=\sqrt{(-3-5{)}^2+(2+4{)}^2}=\sqrt{100}=10\end{array}$

طول القطعة المستقيمة المتوسطة =

$\begin{array}{r}\frac{1}{2}(BC+AD)\\ \frac{1}{2}(5+10)=7.5\end{array}$

جبر: في الشكل المجاور ABCD شبه منحرف أوجد قيمة x بحيث يكون متطابق الساقين في كلٍّ ممَّا يأتي:

27) إذا كان AC = 3x – 7,BD = 2x + 8

الحل:

قطرا شبه المنحرف متطابقة.

$\begin{array}{l}\text{ BD }=\text{ AC }\\ \\ 2\mathrm{x}+8=3\mathrm{x}-7\\ \\ 3\mathrm{x}-2\mathrm{x}=8+7\\ \\ \mathrm{x}=15\end{array}$

28) إذا كان $m\mathrm{\angle }ABC=(4x+11{)}^{\circ },m\mathrm{\angle }DAB=(2x+33{)}^{\circ }$

الحل:

$\begin{array}{l}4x+11=2x+33\\ \\ 4x-2x=33-11\\ \\ 2x=22\\ \\ x=11\end{array}$

جبر: في الشكل المجاور M, P نقطتا منتصفي الساقين لشبه المنحرف QRST.

29) إذا كان QR = 16, PM = 12, TS = 4x فأوجد قيمة .x

الحل:

$\begin{array}{l}PM=\frac{1}{2}(QR+TS)\\ \\ 12=\frac{1}{2}(16+4x)\\ \\ 24=16+4x\\ \\ 4x=24-16\\ \\ 4x=8\\ \\ x=2\end{array}$

30) إذا كان TS = 2x, PM = 20, QR = 6x فأوجد قيمة x

الحل:

$\begin{array}{l}PM=\frac{1}{2}(QR+TS)\\ \\ 20=\frac{1}{2}(6x+2x)\\ \\ 40=6x+2x\\ \\ 40=8x\\ \\ x=5\end{array}$

31) إذا كان PM = 2x, QR = 3x, TS = 10 فأوجد PW.

الحل:

$\begin{array}{l}\mathrm{PM}=\frac{1}{2}(\mathrm{QR}+\mathrm{TS})\\ \\ 2\mathrm{x}=\frac{1}{2}(3\mathrm{x}+10)\\ \\ 4\mathrm{x}=3\mathrm{x}+10\\ \\ \mathrm{x}=10\therefore \mathrm{PM}=2\times 10=20\end{array}$

32) إذا كان TS = 2x + 2, QR = 5x + 3, PM = 13 فأوجد TS

الحل:

$\begin{array}{l}PM=\frac{1}{2}(QR+TS)\\ \\ 13=\frac{1}{2}(5x+3+2x+2)\\ \\ 26=7x+5\\ \\ 7x=26-5\\ \\ 7x=21\\ \\ x=3\\ \\ TS=2x+2\\ \\ TS=6+2=8\end{array}$

تسوق: الوجه الجانبي لحقيبة التسوق المبينة جانباً على شكل شبه منحرف متطابق الساقين إذا كان EC = 9 in, DB = 19 in

$\text{ ، }m\mathrm{\angle }ABE={40}^{\circ },m\mathrm{\angle }EBC={35}^{\circ }$فأوجد كلا مما يأتي:

33) AE

الحل:

$\begin{array}{l}\mathrm{DB}=\mathrm{AC}\\ \\ 19=\mathrm{AE}+\mathrm{EC}\\ \\ 19=\mathrm{AE}+9\\ \\ \mathrm{AE}=19-9\\ \\ \mathrm{AE}=10\mathrm{in}\end{array}$

34) AC

الحل:

$\begin{array}{l}AC=EC+AE\\ \\ AC=9+10\\ \\ AC=19\text{ in }\end{array}$

35) $m\mathrm{\angle }BCD$

الحل:

نظرية الزاويتان المتحالفتان

$\begin{array}{l}\mathrm{m}\mathrm{\angle }\mathrm{ABC}=\mathrm{m}\mathrm{\angle }\mathrm{ABE}+\mathrm{m}\mathrm{\angle }\mathrm{EBC}=40+35={75}^{\circ }\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{ABC}+\mathrm{m}\mathrm{\angle }\mathrm{BCD}={180}^{\circ }\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{ABC}+\mathrm{m}\mathrm{\angle }\mathrm{BCD}={180}^{\circ }\\ \\ 75+\mathrm{m}\mathrm{\angle }\mathrm{BCD}={180}^{\circ }\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{BCD}={105}^{\circ }\end{array}$

36) $m\mathrm{\angle }EDC$

الحل:

بما أن $\overline{AB}\parallel \overline{DC}$ إذن $\mathrm{m}\mathrm{\angle }\mathrm{ABE}=\mathrm{m}\mathrm{\angle }\mathrm{EDC}={40}^{\circ }$ حسب نظرية التبادل داخلياً.

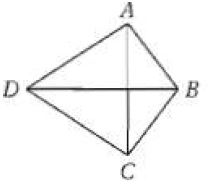
جبر: في الشكل المجاور WXYZ شكل طائرة ورقية.

37) إذا كان $m\angle ZWX = \left(10x\right)° ,m\mathrm{\angle }WXY={120}^{\circ },m\mathrm{\angle }WZY=(4x{)}^{\circ }$ فأوجد $m\angle ZYX$.

الحل:

$\mathrm{m}\mathrm{\angle }\mathrm{ZWX}\cong \mathrm{\angle }\mathrm{ZX}$ (يوجد زوج واحد فقط من الزوايا المتقابلة المتطابقة نظرية 1.26).

لذا $\mathrm{m}\mathrm{\angle }\mathrm{ZYX}=\mathrm{m}\mathrm{\angle }\mathrm{ZWX}=10\mathrm{x}$

وعليه فإن:

$\mathrm{m}\mathrm{\angle }\mathrm{ZWX}+\mathrm{m}\mathrm{\angle }\mathrm{WXY}+\mathrm{m}\mathrm{\angle }\mathrm{ZYX}+\mathrm{m}\mathrm{\angle }\mathrm{WZY}=360$

(مجموع قياسات الزوايا الداخلية للشكل الرباعي) وبالتعويض ينتج:

$\begin{array}{l}10x+120+10x+4x=360\\ \\ 24x+120=360\\ \\ x=10\end{array}$

لذا: $\mathrm{m}\mathrm{\angle }ZYX=10x=10\left(10\right)={100}^{\circ }$

38) إذا كان $m\angle ZWX = (13x +14 )° ,m\mathrm{\angle }WXY={(13x +24 )}^{\circ },m\mathrm{\angle }WZY=35°$ فأوجد $m\angle ZYX$.

الحل:

$m\angle ZWX \cong \angle ZYX$ (يوجد زوج واحد فقط من الزوايا المتقابلة المتطابقة نظرية 1.26).

لذا $\mathrm{m}\mathrm{\angle }\mathrm{ZYX}=\mathrm{m}\mathrm{\angle }\mathrm{ZWX}=13\mathrm{x}+14$

وعليه فإن:

$\mathrm{m}\mathrm{\angle }\mathrm{ZWX}+\mathrm{m}\mathrm{\angle }\mathrm{WXY}+\mathrm{m}\mathrm{\angle }\mathrm{ZYX}+\mathrm{m}\mathrm{\angle }\mathrm{WZY}=360$

(مجموع قياسات الزوايا الداخلية للشكل الرباعي) وبالتعويض ينتج:

$\begin{array}{l}(13x+14)+(13x+24)+(13x+14)+35=360\\ \\ 39x+87=360\\ \\ 39x=360-87\\ \\ x=7\\ \\ \mathrm{\angle }ZYX=13x+14\\ \\ \mathrm{\angle }ZYX={105}^{\circ }\end{array}$

برهان: اكتب برهاناً ذا عمودين.

39) المعطيات: $\overline{XY},\overline{WZ}\cong \overline{ZV},\mathrm{\angle }W\cong \mathrm{\angle }ZXY$ تنصف كلا من $\overline{ZV},\overline{WZ}$

المطلوب: WXYV شبه منحرف متطابق الساقين.

الحل:

المعطيات: $\overline{XY}, \overline{WZ}\cong \overline{ZV}$ تنصف كل من $\overline{ZV},\overline{WZ}$

المطلوب: WXYV شبه منحرف متطابق الساقين.

العبارات (المبررات):

1) $\overline{XY}, \overline{WZ}\cong \overline{ZV}$ تنصف كل من $\overline{ZV},\overline{WZ}$ (معطيات).

2) $\frac{1}{2}WZ=\frac{1}{2}ZV$ (خاصية الضرب).

3) WX = VY (تعريف نقطة المنتصف).

4) $\overline{WX}\cong \overline{VY}$ ( تعريف تطابق القطع المستقيمة).

5) $\mathrm{\angle }\mathrm{W}\cong \mathrm{\angle }\mathrm{ZYY}$ (معطى).

6) $\overline{XY}\parallel \overline{WZ}$ ( اذا كانت الزوايا المتناظرة فإن المستقيمين متوازيان).

7) WXYV شبه منحرف متطابق الساقين (تعريف شبه المنحرف متطابق الساقين)

40) طائرة ورقية: استعن بالطائرة الورقية في الشكل المجاور اكتب باستعمال خصائص شكل الطائرة الورقية برهاناً ذا عمودين
لبيان أن $△MNR$ يطابق $△PNR$

الحل:

المعطيات: MNPQ شكل طائرة ورقية

المطلوب: $△MNR \cong △PNR$

البرهان: العبارات (المبررات):

1) MNPQ شكل طائرة ورقية (معطى).

2) $\overline{\mathrm{NM}}\cong \overline{\mathrm{NP}},\overline{\mathrm{QM}}\cong \overline{\mathrm{PQ}}$ (تعريف شكل الطائرة الورقية).

3) $\overline{\mathrm{QN}}\cong \overline{\mathrm{QN}}$ (خاصية الانعكاس).

4) $\mathrm{\Delta NMQ}\cong \mathrm{\Delta NPQ}$ (SSS).

5) $\mathrm{\angle }\mathrm{MNR}\cong \mathrm{\angle }\mathrm{PNR}$ (العناصر المتناظرة في المثلثين المتطابقين متطابقة).

6) $\overline{\mathrm{NR}}\cong \overline{\mathrm{NR}}$ ( خاصية الانعكاس).

7) $\mathrm{\Delta MNR}\cong \mathrm{\Delta }PNR$ (SAS)

41) أشكال فن: ارسم شكل ڤن يوضح جميع الأشكال الرباعية متضمناً شبه المنحرف المتطابق الساقين وشكل الطائرة الورقية وعموم الأشكال الرباعية التي لا أسماء خاصة لها.

الحل:

هندسة احداثية: حدد ما إذا كان الشكل المعطاة إحداثيات رؤوسه في كل مما يأتي شبه منحرف أم متوازي أضلاع أم مستطيلاً أم مربعاً أم معيناً أم هو شكل رباعي فحسب؟ اختر أكثر المسميات تحديداً ووضح إجابتك.

42) A(-1,4), B(2,6), C(3,3), D(0,1)

الحل:

$\begin{array}{l}\frac{3}{2}=\frac{-3}{-2}=\frac{-1-2}{4-6}=\overline{AB} \mathrm{ميل}\\ \\ \frac{3}{2}=\frac{3-0}{3-1}=\overline{CD} \mathrm{ميل}\\ \\ \frac{-1}{3}=\frac{2-3}{6-3}=\overline{BC} \mathrm{ميل}\\ \\ \frac{-1}{3}=\frac{-1-0}{4-1}=\overline{AD} \mathrm{ميل}\end{array}$

بما أن ميل كل ضلعين متقابلين متساوي إذن الشكل متوازي أضلاع لأن أضلاعه المتقابلة متطابقة ولا يوجد زوايا قائم وأضلاعه المتتالية غير متطابقة.

43) W(-3,4), X(3,4), Y(5,3), Z(-5,1)

الحل:

$\begin{array}{ll}\frac{0}{-6}=\frac{4-4}{-3-3}=\overline{WX} & \mathrm{ميل}\\ & \\ \frac{1}{5}=\frac{2}{10}=\frac{3-1}{5+5}=\overline{YZ}& \mathrm{ميل}\\ & \\ \frac{1}{-2}=\frac{4-3}{3-5}=\overline{XY}& \mathrm{ميل}\\ & \\ \frac{3}{2}=\frac{4-1}{-3+5}=\overline{WZ}& \mathrm{ميل}\\ & \\ \overline{WX}\ne \overline{YZ}\ne \overline{XY}\ne \overline{WZ}& \mathrm{ميل}\end{array}$

إذن شكل رباعي فقط ليس فيه أضلاع متوازية.

44) تمثيلات متعددة: سوف تستقصي في هذه المسألة إحدى خصائص شكل الطائرة الورقية.

a) هندسياً: ارسم قطعة مستقيمة وأنشئ عموداً منصفاً لها لا تنصفه القطعة المستقيمة ولا تساويه طولاً ثم صل أطراف القطعتين المستقيمتين لتكوِّن الشكل الرباعي ABCD كما في الشكل المجاور كرر هذه العملية مرتين وسم الشكلين الرباعيين الجديدين.

الحل:

b) جدولياً: انقل الجدول الآتي وأكمله:

c) لفظياً: اكتب تخميناً حول الشكل الرباعي الذي قطراه متعامدان وغير متطابقين وأحدهما فقط ينصِّف الآخر.

الحل:

إذا كان قطرا شكل رباعي متعامدين وليسا متطابقين وأحد هما فقط ينصف الآخر فإن الشكل الرباعي هو شكل طائرة ورقية.

برهان: اكتب برهاناً إحداثياً لكل من العبارتين الآتيتين:

45) قطرا شبه المنحرف المتطابق الساقين متطابقان.

الحل:

المعطيات: ABCD شبه منحرف متطابق الساقين فيه $\overline{AD}\cong \overline{BC}$

المطلوب: $\overline{BD}\cong \overline{AC}$

البرهان:

$\begin{array}{l}\mathrm{DB}=\sqrt{(\mathrm{a}-\mathrm{b}{)}^2+(0-\mathrm{c}{)}^2}\\ \\ =\sqrt{(\mathrm{a}-\mathrm{b}{)}^2+(\mathrm{c}{)}^2}\\ \\ \mathrm{AC}=\sqrt{\left(\right(\mathrm{a}-\mathrm{b})-0{)}^2+(\mathrm{c}-0{)}^2}\\ \\ =\sqrt{(\mathrm{a}-\mathrm{b}{)}^2+(\mathrm{c}{)}^2}\end{array}$

إذن $\overline{\mathrm{BD}}=\overline{\mathrm{AC}}$ ومن ذلك $\overline{\mathrm{BD}}\cong \overline{\mathrm{AC}}$.

46) القطعة المتوسطة لشبه المنحرف المتطابق الساقين توازي كلاً من القاعدتين.

الحل:

• المعطيات: ABCD شبه منحرف فيه $\overline{XY}$ قطعة متوسطة.
• المطلوب: $\overline{XY}\parallel \overline{AB},\overline{XY}\parallel \overline{DC}$

البرهان:

X نقطة منتصف $\overline{AD}$ وإحداثياتها $\left(\frac{-b}{2},\frac{c}{2}\right)$

Y نقطة منتصف $\overline{BC}$ وإحداثياتها $\left(\frac{2a+b}{2},\frac{c}{2}\right)$

وبما أن ميل $\overline{AB}$ يساوي صفر وميل $\overline{XY}$ يساوي صفر وميل $\overline{DC}$ يساوي صفر فإن $\overline{XY}\parallel \overline{AB},\overline{XY}\parallel \overline{DC}$.