حل أسئلة تدرب وحل المسائل
أوجد ناتج الضرب في كل مما يأتي:
١٢) ب (ب٢ - ١٢ب + ١)
ب (ب٢ - ١٢ب + ١) = ب (ب٢) -١٢ب (ب) + ب
= ب٣ - ١٢ب٢ + ب
١٣) ٢جـ٢(٥جـ٣ - ١٥جـ٢ + ٢جـ + ٢)
المقدار = ٢جـ٢(٥جـ٣ - ١٥جـ٢ + ٢جـ + ٢)
= ٢جـ٢(٥جـ٣) - ٢جـ٢(١٥جـ٢) + ٢جـ٢(٢جـ) + ٢(٢جـ٢)
= ١٠جـ٥ - ٣٠جـ٤ + ٤جـ٣ + ٤جـ٢
١٤) ٢ب ر٢(٢ب ر + ٥ب٢ر - ١٥ب)
المقدار = ٢ب ر٢(٢ب ر + ٥ب٢ر - ١٥ب)
= ٢ب ر٢(٢ب ر) + ٢ب ر٢(٥ب٢ ر) + ٢ب ر٢(-١٥ب)
= ٤ب٢ ر٣ + ١٠ب٣ ر٣ - ٣٠ب٢ ر٢
١٥) ٤ن٣ ل (٢ن٢ ل٢ - ١٠ن ل٤ + ٢)
المقدار = ٤ن٣ ل (٢ن٢ ل٢ - ١٠ن ل٤ + ٢)
= ٤ن٣ ل (٢ن٢ ل٢) - ٤ن٣ ل (١٠ن ل٤) + ٢(٤ن٣ ل)
= ٨ن٥ ل٣ - ٤٠ن٤ ل٥ + ٨ن٣ ل
بسط كل عبارة فيما يأتي:
١٦) -٣(٥س٢ + ٢س + ٩) + س (٢س - ٣)
المقدار = -٣(٥س٢ + ٢س + ٩) + س (٢س - ٣)
= -٣(٥س٢) - ٣(٢س) - ٣(٩) + س (٢س) - س (٣)
= -١٥س٢ -٦س - ٢٧ + ٢س٢ - ٣س
= -١٣س٢ - ٩س - ٢٧
١٧) أ (-٨أ٢ + ٢أ + ٤) + ٣ (٦أ٢ - ٤)
المقدار = أ (-٨أ٢ + ٢أ + ٤) + ٣(٦أ٢ - ٤)
= أ (-٢١٨) + أ (٢أ) + ٤أ + ١٨أ٢ - ١٢
= -٨أ٣ + ٢٠أ٢ + ٤أ - ١٢
١٨) -٤د (٥د٢ - ١٢) + ٧(د + ٥)
المقدار = -٤د (٥د٢ - ١٢) + ٧(د + ٥)
= -٤د (٥د٢) + ٤د (١٢) + ٧د + ٣٥
= -٢٠د٣ + ٥٥د + ٣٥
١٩) -٩جـ (-٢جـ + جـ٢) + ٣(جـ٢ + ٤)
المقدار = -٩جـ (-٢جـ + جـ٢) + ٣(جـ٢ + ٤)
= -٩جـ (-٢جـ) - ٩جـ(جـ٢) + ٣(جـ٢) + ٣(٤)
= -٩جـ٣ + ٢١جـ٢ + ١٢
٢٠) ٤ن (٢ن٣ ب٢ - ٣ن ب٢ + ٥ن) + ٤ب (٦ن٢ ب - ٢ن ب٢ + ٣ب)
المقدار = ٤ن (٢ن٣ ب٢ - ٣ن ب٢ + ٥ن) + ٤ب (٦ن٢ ب - ٢ن ب٢ + ٣ب)
= ٤ن (٢ن٣ ب٢) - ٤ن (٣ن ب٢) + ٤ن(٥ن) + ٤ب (٦ن٢ ب) - ٤ب (٢ن ب٢) + ٤ب(٣ب)
= ٨ن٤ ب٢ + ١٢ن٢ ب٢ + ٢٠ن٢ - ٨ن ب٣ + ١٢ب٢
٢١) سدود: واجهة سد على شكل شبه منحرف، طول قاعدتها السفلية مِثلا ارتفاعها، وقاعدتها العليا أقل من ارتفاعها بـ ١٠ أمتار.
أ) اكتب عبارة لإيجاد مساحة هذه الواجهة.
مساحة شبه المنحرف = نصف (القاعدة السفلى + القاعدة العليا) الارتفاع.
- القاعدة السفلى = ٢ع
- القاعدة العليا = ع - ١٠
المساحة = (٢ع + ع - ١٠) × ع
= ( ع - ١٠) × ع
= ( ع - ٥) × ع
= ع٢ - ٥ع
ب) إذا كان ارتفاع السد ٦٠ متراً، فأوجد هذه المساحة.
المساحة = (٢٦٠) - ٥(٦٠)
= ٣٦٦٠ م٢
حلل كلاً من المعادلات الآتية:
٢٢) ٧(ن٢ + ٥ن - ٩) + ن = ن (٧ن - ٢) + ١٣
٧(ن٢ + ٥ن - ٩) + ن = ن (٧ن - ٢) + ١٣
٧ن + ٣٥ن - ٦٣ + ن = ٧ن - ٢ن + ١٣
٣٦ن - ٦٣ = -٢ن + ١٣
٣٨ن = ١٣+ ٦٣
ن = ٧٦ ÷ ٣٨
ن = ٢
٢٣) ٥(٤ع + ٦) - ٢(ع - ٤) = ٧ع (ع + ٤) - ع (٧ع - ٢) - ٤٨
٥(٤ع + ٦) - ٢(ع - ٤) = ٧ع (ع + ٤) - ع (٧ع - ٢) - ٤٨
٢٠ع + ٣٠ - ٢ع + ٨ = ٧ع٢ + ٢٨ - ٧ع٢ + ٢ع - ٤٨
١٨ع + ٣٨ = ٢ع - ٢٠
١٨ع - ٢ع = - ٢٠ - ٣٨
١٦ع = - ٥٨
ع =
ع =
٢٤) ٩جـ (جـ - ١١) + ١٠(٥جـ - ٣) = ٣جـ (جـ + ٥) + جـ (٦جـ - ٣) - ٣٠
٩جـ (جـ - ١١) + ١٠(٥جـ - ٣) = ٣جـ (جـ + ٥) + جـ (٦جـ - ٣) - ٣٠
٩جـ٢ - ٩٩ + ٥٠جـ - ٣٠ = ٣جـ ٢+ ١٥ + ٦جـ٢ - ٣جـ - ٣٠
٩جـ٢ - ٣جـ٢ - ٦جـ٢ - ٥٠جـ + ٣جـ = ٣٠ - ٣٠
٦جـ٢ - ٦جـ٢ - ٤٧جـ = ٠
- ٤٧جـ = ٠
جـ = ٠
٢٥) ٢ن (٥ن - ٢) - ١٠(ن٢ - ٣ن + ٦) = -٨ن (ن + ٤) + ٤(٢ن٢ - ٧ن)
١٠ن٢ - ٤ن - ١٠ن٢ + ٣٠ن - ٦٠ = - ٨ن٢ - ٣٢ن + ٨ن٢ - ٢٨ن
٢٦ن - ٦٠ = -٣٢ن - ٢٨ن
٢٦ن - ٦٠ = ٦٠
٨٦ن = ٦٠
ن =
بسط كل عبارة فيما يأتي:
٢٦) ن ب٢(٣٠ب٢ + ٩ن٢ ب - ١٢)
المقدار = ن ب٢ (٣٠ب٢) + ن ب٢ (٩ن٢ ب) + ١٢(-ن ب٢)
= ٢٠ن ب٤ + ٦ن٣ ب٣ - ٨ن ب٢
٢٧) ر٢ ل (١٠ر٣ + ٥رل٣ + ١٥ل٢)
المقدار = ر٢ ل (١٠ر٣) + ر٢ ل (٥ر ل٣) + ر٢ ل (١٥ل٣)
= ٦ر٥ ل + ٣ر٣ ل٤ + ٩ر٢ ل٣
٢٨) - س٢ ع (٢ع٢ + ٤س ع٣) + س ع٢(س ع + ٥س٣ ع) + س٢ ع٣(٣س٢ ع + ٤س ع)
المقدار = - س٢ ع (٢ع٢) - س٢ ع (٤س ع٣) + س ع٢(س ع) + س ع٢(٥س٣ ع) س٢ ع٣(٣س٢ ع) + س٢ ع٣(٤س ع)
= - ٢ع٣ س٢ - ٤س٣ ع٤ + س٢ ع٣ + ٥س٤ ع٣ + ٣س٤ ع٤ + ٤س٣ ع٤
= -ع٣ س٢ + ٥س٤ ع٣ + ٣س٤ ع٤
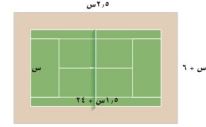
٢٩) تنس أرضي: يبني نادي التنس ملعباً جديداً يحيط به ممر منتظم، كما في الشكل المجاور.
أ) اكتب عبارة تمثل مساحة ملعب التنس
مساحة الملعب = الطول × العرض
= (١,٥ + ٢٤) × س
= ١,٥س٢ + ٢٤س
ب) اكتب عبارة تمثل مساحة الممر.
مساحة الملعب = الطول × العرض.
= (١,٥س + ٢٤) × س
= ١,٥س٢ + ٢٤س
٣٠) تمثيلات: ستستكشف في هذه المسألة درجة ناتج ضرب وحيدة حد في كثيرة حدود.
أ) جدولياً: اكتب ثلاث وحيدات حد مختلفة الدرجات وثلاث كثيرات حدود مختلفة الدرجات، ثم حدد درجة كل وحيدة حد وكثيرة حدود، واضرب وحيدات الحد في كثيرات الحدود، وحدد درجة ناتج الضرب، وأخيراً سحب نتائجك في الجدول على النحو الآتي:
| وحيدات الحد | الدرجة | كثيرة الحدود | الدرجة | ناتج ضرب وحيدة الحد في كثيرات الحدود | الدرجة |
| ٢س | ١ | س٢ -١ | ٢ | ٢س٣ -٢س | ٣ |
| ٣س٢ | ٢ | س٥ + ١ | ٥ | ٣س٧ + ٣س٢ | ٧ |
| ٤س٣ | ٣ | س٦ + ١ | ٦ | ٤س٩ + ٤س٣ | ٩ |
ب) لفظياً: خمن درجة ناتج ضرب وحيدة حد في كثيرة حدود، ما درجة ناتج وحيدة حد من الدرجة أ، في كثيرة حدود من الدرجة ب؟
درجة ناتج الضرب هي مجموع درجتي وحيدة الحد وكثيرة الحدود أ + ب.
٣١) تحد: أوجد قيمة ب التي تجعل ٣س ب(٤س٢ب + ٣ + ٢س٣ب - ٢) = ١٢س١٢ + ٦س١٠
٣س ب(٤س٢ب + ٣ + ٢س٣ب - ٢) = ١٢س١٢ + ٦س١٠
(٣س ب) (٤س٢ب+٣) + (٣س ب) (٢س٣ب-٢) = ١٢س١٢ + ٦س١٠
١٢س+٢ب+٣+ب + ٦س-٢+٣ب+ب = ١٢س١٢ + ٦س١٠
١٢س٣ب+٣ + ٦س٤ب-٢ = ١٢س١٢ + ٦س١٠
بالمقارنة نجد أن ٣ب + ٣ = ١٢
٣ب = ٩
ب = ٣
٣٢) تبرير: هل توجد قيمة للمتغير س تجعل العبارة: (س + ٢)٢ = س٢ + ٢٢ صحيحة؟ وإذا كان كذلك، فأوجد هذه القيمة، وفسر إجابتك.
نعم، صفر عند تعويض بدلاً من س في المعادلة فكلا الطرفين يساوي ٢٢ = ٤ وهذا يجعل المعادلة صحيحة.
٣٣) مسألة مفتوحة: اكتب وحيدة حد وكثيرة حدود باستعمال المتغير نفسه، أوجد ناتج ضربهما.
٣ن، ٤ن + ١، ١٢ن + ٣ن
٣٤) اكتب: صف خطوات ضرب وحيدة حد في كثيرة حدود.
لضرب وحيدة حد في كثيرة حدود استعمل خاصية التوزيع اضرب وحيدة الحد في كل حد في كثيرة الحدود ثم بسط بضرب المعاملات معاً واستعمال خاصية ضرب القوى للمتغيرات.
٣٥) يبيع محل ملابس بنطالاً، وقميصاً أسبوعياً، فإذا كان ثمن القميص ٨٠ ريالاً، والبنطال ١٢٠ ريالاً، فأي العبارات الآتية تمثل المبلغ الذي يحصل عليه المحل ثمناً لذلك؟
أ) ٨٠م + ١٢٠ن
ب) ١٢٠م + ٨٠ن
جـ) ٢٠٠(م + ن)
د) ٩٦٠٠م ن
٣٦) إذا كانت أ = ٥س + ٧ص، ب = ٢ص - ٣س، فأوجد أ + ب.
أ) ٢س - ٩ص
ب) ٣ص + ٤س
جـ) ٢س + ٩ص
د) ٢س - ٥ص

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات