حل أسئلة تدرب وحل المسائل
١١) (أ + ١٠) (أ + ١٠)
(أ + ١٠) (أ + ١٠ = (أ + ١٠)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = أ٢ + ٢٠أ + ١٠٠
١٢) (ب - ٦) (ب - ٦)
(ب - ٦) (ب - ٦) = (ب - ٦)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ب٢ - ١٢ب + ٣٦
١٣) (هـ + ٧)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = هـ٢ + ١٤هـ + ٤٩
١٤) (س + ٦)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = س٢ + ١٢س + ٣٦
١٥) (٨ - م)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ٦٤ - ١٦م + م٢
١٦) (٩ - ٢ص)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ٨١ - ٣٦ص + ٤ص٢
١٧) (٢ب + ٣)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ٤ب٢ + ١٢ب + ٩
١٨) (٥ن - ٢)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ٢٥ن٢ - ٢٠ن + ٤
١٩) (٨هـ - ٤ن)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = ٦٤هـ٢ - ٦٤هـ ن + ١٦ن٢
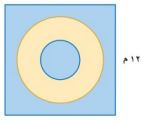
٢٠) مصارعة: تكون سجادة في العادة مربعة الشكل، طول ضلعها ١٢ متراً تقريباً، وتحتوي على دائرتين كما في الشكل المجاور، افترض أن نصف قطر الدائرة الداخلية (ر) متر، وأن نصف قطر الدائرة الخارجية يزيد على نصف قطر الدائرة الداخلية بـ ٣ أمتار.
أ) اكتب عبارة تمثل مساحة الدائرة الكبرى.
مساحة الدائرة الكبرى = ط نق٢
= ط (ر + ٣)٢
= ط (ر٢ + ٩ + ٦ر)
= ط ر٢ + ٦ط ر + ٩ط
ب) اكتب عبارة تمثل مساحة جزء المربع خارج الدائرة الكبرى.
مساحة المربع = طول الضلع × نفسه:
= ١٢ × ١٢ = ١٤٤
= ١٤٤ -(ط ر٢ + ٦ط ر + ٩ط)
= ١٤٤ -(ط ر٢ + ٦ط ر + ٩ط)
أوجد ناتج كل مما يأتي:
٢١) (ل + ٣) (ل - ٣)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(ل + ٣) (ل - ٣) = ل٢ - ٩
٢٢) (٤ - س) (٤ + س)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(٤ - س) (٤ + س) = ١٦ - س٢
٢٣) (٢ك + ٥ر) (٢ك - ٥ر)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(٢ك + ٥ر) (٢ك - ٥ر) = ٤ك٢ - ٢٥ر٢
٢٤) (٣أ + ٧ب) (٣أ - ٧ب)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(٣أ٢ + ٧ب) (٣أ٢ - ٧ب) = ٩أ٤ - ٤٩ب٢
أوجد ناتج كل مما يأتي:
٢٥) (٥ص + ٧)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
(٥ص + ٧)٢ = ٢٥ص٢ + ٧٠ص + ٤٩
٢٦) (٨ - ١٠أ)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
(٨ - ١٠أ)٢= ٦٤ - ١٦٠أ + ١٠٠أ٢
٢٧) (٣ن + ١٢) (٣ن - ١٢)
(أ٢ + ب)٢ = (أ - ب) (أ + ب)
(٣ن + ١٢) (٣ن - ١٢) = ٩ن٢ - ١٤٤
٢٨) (أ + ٤ب)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
(أ + ٤ب)٢ = أ٢ + ٨أ ب + ١٦ب٢
٢٩) (٣ك - ٥ر)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
(٣ك - ٥ر)٢= ٩ك٢ - ٣٠ك ر + ٢٥ر٢
٣٠) (٢جـ - ٩د)٢
(أ - ب)٢ = أ٢ + ٢أ ب + ب٢
(٢جـ - ٩د)٢= ٤جـ٢ - ٣٦جـ د + ٨١د٢
٣١) (٣أ٤ - ب) (٣أ٤ + ب)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(٣أ٤ - ب) (٣أ٤ + ب) = ٩أ٨ - ب٢
٣٢) (٥س٢ - ص٢)٢
(أ - ب)٢ = أ٢ + ٢أ ب + ب٢
(٥س٢ - ص٢)٢= ٢٥س٤ - ١٠س٢ ص٢ + ص٤
٣٣) (٨أ٢ - ٩ب٣) (٨أ٢ + ٩ب٣)
(أ٢ - ب)٢ = (أ - ب) (أ + ب)
(٨أ٢ - ٩ب٣) (٨أ٢ + ٩ب٣) = ٦٤أ٤ - ٨١ب٦
٣٤) (ك + ٨)٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
(ك + ٨)٢= ك٢ + ١٢ك + ٦٤
٣٥) (ص - ٤)٢
(أ - ب)٢ = أ٢ + ٢أ ب + ب٢
(ص - ٤)٢= ص٢ - ص + ١٦
٣٦) (٧ع٢ + ٥ص٢) (٧ع٢ - ٥ص٢)
(أ٢ - ب٢) = (أ - ب) (أ + ب)
(٧ع٢ + ٥ص٢) (٧ع٢ - ٥ص٢) = ٤٩ع٤ - ٢٥ص٤
٣٧) (٢م + ٣) (٢م - ٣) (م + ٤)
المقدار = [(٢م + ٣) (٢م - ٣)] (م + ٤)
(أ٢ - ب٢) = (أ - ب) (أ + ب)
المقدار = (٤م٢ - ٩) (م + ٤)
= ٤م٢ (م) + ٤م٢ (٤) + (-٩) (م) + (-٩) (٤)
= ٤م٣ + ١٦م٢ - ٩م - ٣٦
٣٨) (ر + ٢) (ر - ٢) (ر + ٥)
المقدار = [(ر + ٢) (ر - ٢)] [(ر - ٥) (ر + ٥)]
= (ر٢ - ٤) (ر٢ - ٢٥)
= (ر٢) (ر٢) + (ر٢) (-٢٥) + (-٤) (ر٢) + (-٤) (٢٥)
= ر٤ - ٢٥ر٢ - ٤ر٢ - ١٠٠
٣٩) هندسة: اكتب كثيرة حدود تمثل مساحة الشكل أدناه.
مساحة الشكل = مجموع مساحتي المربعين:
مساحة الشكل = (س - ١)٢ (س + ٢)٢
(أ - ب)٢ = أ٢ + ٢أ ب + ب٢
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
مساحة الشكل = (س٢ - ٢س + ١) + (س٢ + ٤س + ٤)
= ٢س٢ + ٢س + ٥
أوجد ناتج كل مما يأتي:
٤٠) (جـ + د) (جـ + د) (جـ + د)
المقدار = (جـ + د) (جـ + د)
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = (جـ٢ + د٢ + ٢جـ د) (جـ + د)
= جـ + جـ د + ٢جـ د + د جـ + د + ٢جـ د
= جـ٣ + ٣جـ٢ د + ٣جـ د٢ + د٣
٤١) (٢أ - ب)٣
المقدار = (٢أ - ب)٢ (٢أ - ب)
(أ - ب)٢ = أ٢ - ٢أ ب + ب٢
المقدار = (٤أ٢ + ب٢ - ٤أ ب) (٢أ - ب)
= ٨أ٣ + ٢أ ب٢ - ٨أ٢ ب - ٤أ٢ ب - ب٣ + ٤أ ب٢
= ٨أ٢ - ٢أ٢ ب + ٦أ ب٢ - ب٣
٤٢) (ف + جـ) (ف - جـ) (ف + جـ)
(أ - ب)٢ = أ٢ - ٢أ ب + ب٢
المقدار = (ف٢ - جـ٢) (ف + جـ)
= (ف٢) (ف) + (ف٢) (جـ) + (-جـ٢) (ف) + (-جـ٢) (ج)
= ف٣ + ف٢ جـ - ف جـ٢ - جـ٣
٤٣) (ك - م) (ك + م) (ك - م)
(أ٢ - ب٢) = (أ - ب) (أ + ب)
المقدار = (ك٢ - م٢) (ك - م)
= ك٣ - ك٢ م - ك م٢ + م٣
٤٤) (ن - ب)٢ (ن + ب)
(أ - ب)٢ = أ٢ - ٢أ ب + ب٢
المقدار = (ن - ٢ن ب + ب) (ن + ب)
= ن٣ + ن ب٢ - ٢ن٢ ب + ب ن٢ + ب٣ - ٢ن ب٢
= ن٣ - ن٢ ب - ن ب٢ + ب٣
٤٥) (ك + ر)٢ (ك - ر)
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = (ك٢ + ٢ك ر + ر٢) (ك - ر)
= ك٣ + ر٢ ك + ٢ك٢ ر - ر ك٢ - ر٣ -٢ك ر٢
= ك٣ + ك٢ ر - ك ر٢ - ر٣
٤٦) تمثيلات متعددة: سوف تكتشف في هذه المسألة قاعدة تمثل حاصل ضرب مجموع حدين في الفرق بينهما، أبدأ بورقة مربعات، وارمز إلى طول كل ضلع في المربع بالرمز أ، ثم ارسم مربعاً صغيراً في إحدى زواياه، وارمز إلى طول ضلعه بالرمز ب.
أ) عددياً: أوجد مساحة كل مربع.
مساحة المربع الكبير تساوي أ٢ ومساحة المربع الصغير تساوي ب٢
ب) حسياً: قص المربع الصغير من الزاوية، ما مساحة الشكل المتبقية؟
مساحة المربع أ - مساحة المربع ب
المساحة المتبقية = أ٢ - ب٢
جـ) تحليلياً: أفصل المستطيل السفلي، ثم دوره واسحبه إلى جوار المستطيل العلوي، ما طول المستطيل في التمثيل الجديد؟ وما عرضه؟ وما مساحته؟
مساحة المستطيل = (أ + ب) (أ - ب)
= أ٢ - ب٢
د) تحليلياً: ما القاعدة التي توصلت إليها من الفقرتين ب، جـ؟
القاعدة: (أ + ب) (أ - ب) = أ٢ - ب٢
٤٧) حدد العبارة المختلفة عن العبارات الثلاث الأخرى فيما يأتي:
(٢جـ - د) (٢جـ - د) ناتج الضرب لا يحتوي على حد أوسط بينما الحدود الثلاثة الأخرى تحتوي على حد أوسط.
٤٨) تحد: هل يوجد قاعدة لمكعب المجموع (أ + ب)؟
أ) استقص إجابة هذا السؤال بإيجاد ناتج: (أ + ب) (أ + ب) (أ + ب).
نعم،
المقدار = (أ + ب)٢ (أ + ب)
(أ + ب)٢ = أ٢ + ٢أ ب + ب٢
المقدار = (أ٢ + ٢أب + ب٢) (أ + ب)
ب) استعمل القاعدة التي وجدتها في الفرع أ لإيجاد ناتج: (س + ٢)٣.
المقدار = (س + ٢)٢ (س + ٢)
٤٩) تبرير: أوجد قيمة جـ التي تجعل من العبارة ٢٥س - ٩٠س + جـ مربعاً كاملاً.
٥ × ٢ × u جـ = ٩٠
١٠ uجـ = ٩٠
uجـ = ٩٠ ÷ ١٠
uجـ = ٩
(uجـ)٢ = (٩)٢
جـ = ٨١
٥٠) اكتب: صف كيف تجد مربع مجموع حدين ومربع الفرق بين حدين، وكيف تجد ناتج ضرب مجموع حدين في الفرق بينهما.
- لإيجاد مربع المجموع طبق طريقة التوزيع بالترتيب أو طبق النمط.
- مربع مجموع أحاديتي حدود هو مربع الحد الأول زائد مثلي حاصل ضرب الحدين، زائد مربع الحد الثاني.
- ومربع الفرق بين أحاديتي حدود، هو مربع الحد الأول، ناقص مثلي حاصل ضرب الحدين، زائد مربع الحد الثاني.
- وحاصل ضرب المجموع والفرق للكميتين نفسيهما، هو مربع الحد الأول ناقص مربع الحد الثاني.
٥١) ما ناتج ضرب (٢أ - ٣) (٢أ - ٣)؟
أ) ٤ا + ١٢أ + ٩
ب) ٤أ + ٩
جـ) ٤أ - ١٢أ - ٩
د) ٤أ - ١٢أ + ٩
المقدار = (٢أ - ٣)٢
(أ - ب)٢ = أ٢ - ٢أ ب + ب٢
= ٤أ - ١٢أ + ٩
٥٢) يقطع مروان مسافة ٦ كلم في م دقيقة بسيارته، كم دقيقة سيحتاج إليها بقطع ٣٠ كلم بهذا المعدل؟
أ) م
ب) ١٨٠م
جـ) ٥م
د)
عدد الدقائق = = ٥م

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)


النقاشات