حل أسئلة تدرب وحل المسائل
حدد ما إذا كان كل زوج من المثلثات في الأسئلة الآتية متشابهين أم لا، وبرر إجابتك:
٨) .JPG)
لا، قياسات الزوايا غير متساوية.
٩) .JPG)
لا، الأضلاع غير متناسبة.
١٠) .JPG)
نعم، الأضلاع متناسبة.
١١) .JPG)
لا، قياسات الزوايا غير متساوية.
١٢) .JPG)
لا، الأضلاع غير متناسبة.
- ٢
- = ٢
١٣) .JPG)
نعم، قياسات الزوايا متساوية.
في الأسئلة ١٤ - ١٨، إذا كان م ك هـ ر ت و، فأوجد قياسات العناصر المجهولة:
١٤) مَ = ٢، كَ = ٧، هـَ = ٦، رَ = ٤
- ت =
ت = ١٤
- و =
و = ١٢
١٥) رَ = ٧,٥، وَ = ١٥، تَ = ٢٠، هـَ = ٦
- ك =
ك = ٨
- م =
م = ٣
١٦) مَ = ٣,٥، كَ = ٩، تَ = ٦، هـَ = ٤
- هـَ =
هـَ = ٦,٥
- رَ =
رَ = ٥,٢٥
١٧) مَ = ١,٤، هـَ = ٢,٨، وَ = ٠,٥٦، تَ = ٠,٨٤
- رَ =
رَ = ٠,٢٨
- كَ =
كَ = ٤,٢
١٨) مَ = ، ك َ = ، تَ = ، وَ =
رَ = = ٢
هـَ =
هـَ =
١٩) ألعاب: يستعمل تصميم نموذج المركبات المقياس ١سم: ٠,٢٤م من الطول الفعلي للمركبة، إذا للمركبة الأصلية نافذة على شكل مثلث قائم الزاوية، ارتفاعها ٠,٧٦ م فكم سيكون ارتفاع النافذة على النموذج؟
ع = = ٣,٢
ع = ٣,٢ سم تقريباً.
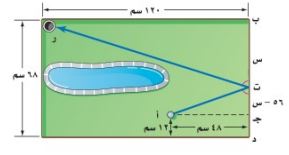
٢٠) جولف: يلعب حمد لعبة جولف مصغرة كما في الشكل المجاور، ويريد قذف الكرة من النقطة أ إلى النقطة ت لترتد وتدخل الحفرة ر، استعمل تشابه المثلثات لتحديد بعد نقطة الارتداد عن الرأس ب.
٦٧٢٠ - ١٢٠س = ٤٨س
٦٧٢٠ = ٤٨س + ١٢٠س
س = ٤٠ سم.
٢١) خرائط: يظهر مقياس رسم لخريطة المملكة أن ٢,٥ سم على الخريطة تمثل ١٠٠ كيلو متر في الواقع، فإذا كانت المسافة بين مكة المكرمة والمدينة المنورة على الخريطة ٨ سم، فما البعد الحقيقي بينهما؟
ف = = ٣٢٠ البعد الحقيقي بينهما = ٣٢٠ كلم.
٢٢) مشروع المدرسة: خطط معلم التاريخ لعمل نموذج للكعبة المشرفة على مقياس رسم ٥ سم، ٠,٦م، فإذا كان الارتفاع الفعلي للكعبة المشرفة ١٤ م، فكم سيكون ارتفاع النموذج؟
ف =
ف =
ف ≈ ١,١٦٦٧ م.
ارتفاع النموذج = ١,١٦٦٧ سم تقريباً.
٢٣) اكتشف الخطأ: قارنت رهف ونوال بين المثلثين المتشابهين المجاورين، فأيهما كانت مقارنتها صحيحة؟ فسر إجابتك.
مقارنة كلتاهما خطأ، فالأقواس تشير إلى الزوايا المتناظرة لذا فإن المثلثين متشابهين.
٢٤) تحد: المثلث س ص ز يشابه المثلثين المتشابهين المكونين من القطعة المستقيمة العمودية الواصلة بين ز والقطعة المستقيمة س ص، اكتب ثلاث عبارات تتعلق بهذين المثلثين، ولم تتشابه؟
س ص ز س ز و
س ص ز ز ص و
س ز و ز ص و
المثلثات متشابهة لأن قياسات الزوايا المتناظرة متساوية.
٢٥) تبرير: حدد ما إذا كانت العبارة الآتية صحيحة دائماً، أم صحيحة أحياناً، أم غير صحيحة أبداً؟ فسر إجابتك.
"إذا ضربت أطول أضلاع مثلث في ٣، فإن زوايا المثلث بعد تكبيره لها نفس قياسات زوايا المثلث الأصلي"
صحيحة دائماً، فالأضلاع متناسبة بمقياس معامله ٣ والذي يعني أن المثلثات متشابهة والزوايا دائماً والزوايا دائماً متطابقة.
٢٦) مسألة مفتوحة: ارسم مثلثاً وسمه أ ب جـ، ثم ارسم المثلث المشابه له وسمه وك ر، على أن تكون مساحته ٤ أمثال أ ب جـ، واشرح استراتيجيتك،
طول قاعدة و ك ر مثلاً ارتفاع أ ب جـ، المثلثات متشابهان لأن زواياهما المتناظرة متطابقة.
٢٧) اكتب: لخص كيف تحدد أن المثلثين متشابهان؟ وكيف تجد القياسات المجهولة فيهما؟
يكون المثلثات متشابهين إذا كانت زواياهما المتناظرة متناسبة وإذا كان المثلثان متشابهين فيمكن استعمال التناسب لإيجاد أطوال الأضلاع المجهولة وإذا كانت الزوايا مجهولة فحدد قياس زاوية في أحد المثلثين المتشابهين فيكون للزاوية المناظرة لها من المثلث الآخر القياس نفسه.
٢٨) أوجد المسافة بين النقطتين (٢، -٤)، (-٥، ٨).
أ)
ب)
جـ)
د)
ف =
ف =
ف =
الاختيار الصحيح د)
٢٩) أي المعادلات الآتية تمثل مستقيماً الصادي -٤، وميله ٦؟
أ) ص = ٦س - ٤
ب) ص = -٤س + ٦
جـ) ص = -٦س + ٤
د) ص = ٦س + ٤

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات