حل أسئلة تدرب وحل المسائل
أوجد قيم النسب المثلثية للزاوية ب في كل مما يأتي:
١٥) .JPG)
أ جـ = = ١٥ حسب نظرية فيثاغورس.
جا ب = ، جتا ب = ، ظا ب =
١٦) .JPG)
أ ب = = ١٣ حسب نظرية فيثاغورس.
جا ب = ، جتا ب = ، ظا ب =
١٧) .JPG)
أ جـ =
= ٤
- جا ب =
- جتا ب =
- ظا ب =
استعمل الحاسبة لإيجاد قيمة كل نسبة مثلثية فيما يأتي، مقربة إلى أقرب جزء من عشرة آلاف:
١٨) ظا ٢°
ظا ٢° = ٠,٠٣٤٩
١٩) جا ٨٩°
جا ٨٩° = ٠,٩٩٩٨
٢٠) جتا ٤٤°
جتا ٤٤° = ٠,٧١٩٣
٢١) ظا ٤٥°
ظا ٤٥° = ١
٢٢) جا ٧٣°
جا ٧٣° = ٠,٩٥٦٣
٢٣) جتا ٩٠°
جتا ٩٠° = ٠
٢٤) جا ٣٠°
جا ٣٠° = ٠,٥
٢٥) ظا ٦٠°
ظا ٦٠° = ١,٧٣٢١
حل كل مثلث قائم فيما يأتي مقرباً طول كل ضلع إلى أقرب جزء من عشرة:
٢٦) .JPG)
قµ ص = ١٨٠ - (٤٧ + ٩٠) = ٤٣°
جا (٤٧°) =
ص س = ١٦ ÷ جا(٤٧°) ≈ ٢١,٩
ظا (٤٧°) =
ع س = ١٦ ÷ ظا (٤٧°) = ١٤,٩
٢٧) .JPG)
قµ جـ = ١٨٠ - (٦٨ + ٩٠) = ٢٢°
جا (٦٨°) =
ك جـ = ٩ × جا (٦٨°) = ٨,٣
جتا (٦٨°) =
ك ل = ٩ × جتا (٦٨°) = ٣,٤
٢٨) .JPG)
قµ ر = ١٨٠ - (١٤ + ٩٠) = ٧٦°
ظا (١٤°) =
ب ر = ٧ × ظا (١٤) = ١,٧
جتا (١٤°) =
ر جـ = ٧ ÷ جتا (١٤°) = ٧,٢
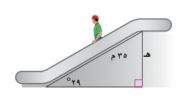
٢٩) سلم كهربائي: يبلغ طول السلم الكهربائي في أحد الأسواق الكبيرة ٣٥ متراً، وقياس الزاوية التي يكونها مع الأرض ٢٩°، أوجد ارتفاع السلم.
جا (٢٩°) =
هـ = ٣٥ × جا (٢٩°)
هـ ≈ ١٧ متر تقريباً.
أوجد قجـ لكل قائم الزاوية فيما يأتي مقرباً إلى أقرب درجة:
٣٠) .JPG)
ظا (µ جـ) = ، ق µ جـ = ٣١°
٣١) .JPG)
جتا (µ جـ) = ، ق µ جـ = ٧٢°
٣٢) .JPG)
جتا (µ جـ) = ، ق µ جـ = ٥٠°
٣٣) وقف الملك عبد العزيز: يصل ارتفاع أبراج وقف الملك عبد العزيز المطلة على المسجد الحرام إلى ٤٠٠ متر، ينظر عمار إلى الأبراج بزاوية ٥٥°، فما بعد عمار عن قاعدة الأبراج؟
ظا (٥٥°) =
ف = ٤٠٠ ÷ ظا (٥٥°) ≈ ٢٨٠ متر تقريباً.
٣٤) غابات: يقدر حارس غابة شجرة بنحو ٥٠ متراً، فإذا كان الحارس يقف على بعد ٣٠ متراً من قاعدة الشجرة، فما مقياس الزاوية التي يشكلها مع قمة الشجرة؟
نفرض أن الزاوية التي يشكلها مع قمة الشجرة (س)
ظا (µ س) =
إذن الزاوية التي يشكلها مع قمة الشجرة = ٥٩° تقريباً.
في السؤالين ٣٥ - ٣٦، افترض أن أ زاوية حادة في المثلث القائم أ ب جـ، ثم أوجد:
٣٥) جا أ، ظا أ إذا كان جتا أ =
المقابل = حسب نظرية فيثاغورس.
جا أ = ، ظا أ =
٣٦) ظا أ جتا أ إذا جا أ = ,
ظا أ = ، جتا أ =
المجاور = حسب نظرية فيثاغورس.
ظا أ =
جتا أ =
٣٧) تمثيلات متعددة: سوف تكتشف في هذه المعادلة المسألة العلاقة بين دوال الجيب ودوال جيب التمام.
أ) جدولياً: انقل الجدول الآتي وأكمله مستعملاً المثلثات أعلاه:
| المثلث | النسب المثلثية | جا٢ | جتا٢ | جا٢+جتا٢ = | |
| أ ب جـ | جا أ = | جتا أ = | جا٢ أ = | جتا٢ أ = | ١ |
| جا جـ = | جتا جـ = | جا٢ جـ = | جتا٢ جـ = | ١ | |
| هـ ك ل | جا هـ = | جتا هـ = | جا٢ هـ = | جتا٢ هـ = | ١ |
| جا ل = | جتا ل = | جا٢ ل = | جتا٢ ل = | ١ | |
| س ص ز | جا س = | جتا س = | جا٢ س = | جتا٢ س = | ١ |
| جا ز = | جتا ز = | جا٢ ز = | جتا٢ ز = | ١ | |
ب) لفظياً: أخمن علاقة مجموع مربعي دالتي الجيب وجيب التمام لزاوية حادة في مثلث قائم الزاوية.
لفظياً: مجموع مربعي جيب الزاوية الحادة وجيب تمامها في مثلث قائم الزاوية يساوي ١.
٣٨) غواصات: إذا نزلت غواصة مسافة ٣ أميال قطرياً بزاوية مقدارها ١٠° مع قاع محيط، فكم يصبح بعدها عن سطح الماء؟
جا (١٠°) = المقابل ÷ الوتر.
جا (١٠°) = المقابل ÷ ٣
المقابل (بعد الغواصة عن سطح الماء) = جا (١٠°) × ٣ = ٠,٥ ميل تقريباً.
٣٩) تحد: حل المثلث في الشكل المجاور.
١٨٠-(١٢ أ + ٧ + ٦أ - ٣ + ٩٠) = ٠
١٨٠ - (١٨أ + ٩٤) = ٠
١٨٠ - ١٨أ - ٩٤ = ٠
-١٨أ + ٨٦ = ٠
أ = ٨٦ ÷ ١٨ = ٤,٧٨
(٣جـ - ٢)٢ = جـ٢ + (جـ + ٧)٢
٩جـ٢ + ٤ - ١٢جـ = جـ٢ + جـ٢ + ٤٩ + ١٤جـ
٩جـ٢ + ٤ - ١٢جـ - جـ٢ - جـ٢ - ٤٩ - ١٤جـ =٠
٧جـ٢ - ٢٦جـ - ٤٥ = ٠
جـ =
جـ =
جـ = = ٥
٤٠) تبرير: استعمل تعريف نسب الجيب وجيب التمام في تعريف نسبة الظل.
= ظا أ
٤١) مسألة مفتوحة: اكتب مسألة تستعمل فيها نسبة جيب التمام لإيجاد قياس زاوية مجهولة في مثلث قائم الزاوية، ثم حلها.
أوجد قياس الزاوية المجهولة في المثلث أ ب جـ القائم الزاوية في ب إذا كان أ جـ = ، أ ب = ٢
قµ أ = ٥٦°
٤٢) تبرير: إذا كان جيب الزاوية وجيب تمامها متساويين، فماذا تستنتج عن المثلث؟
المثلث متطابق الضلعين وقائم الزاوية إذن فالضلعان متساويان.
٤٣) اكتب: وضح كيف يمكن استعمال النسب المثلثية لإيجاد أطوال الأضلاع المجهولة في مثلث علم فيه قياس زاوية حادة وطول أحد الأضلاع.
تستعمل الزاوية المعطاة وقياس طول الضلع في المثلث القائم الزاوية في كتابة إحدى النسب المثلثية حيث تستعمل نسبة جيب التمام الضلع المجاور والوتر وتستعمل نسبة الظل الضلع المقابل والضلع المجاور.
٤٤) أي المتباينات الآتية تعبر عن التمثيل البياني أدناه؟
أ) -٢ س ٤
ب) -٢ < س < ٤
جـ) س ٤ أو س -٢
د) س > ٤ أو س < -٢
٤٥) إجابة قصيرة: يتقاضى مندوب مبيعات ٦٤٠٠٠ ريال راتباً سنوياً، لإضافة إلى ٥٪ من قيمة مبيعاته، ما قيمة المبيعات التي عليه بيعها ليزيد دخله السنوي حتى ٩٠٠٠٠ ريال؟
الفرق بين الدخلين = ٩٠٠٠٠ - ٦٤٠٠٠ = ٢٦٠٠٠
قيمة المبيعات لزيادة الدخل = = ٥٢٠٠٠٠
أكثر من ٥٢٠٠٠٠ ريال.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات