اختبار منتصف الفصل
أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعات المحدبة الآتية: (الدرس 1-1).
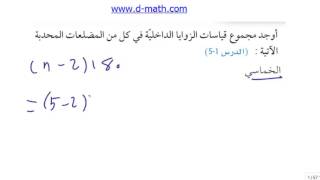
1) الخماسي:
الحل:
2) السباعي:
الحل:
3) ذو 18 ضلعاً:
الحل:
4) ذو 23 ضلعاً:
الحل:
أوجد قياسات جميع الزوايا في كل من المضلعين الآتيين: (الدرس 1-1).
5)
الحل:
6)
الحل:
أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه الداخلية في كل مما يأتي:
7) 720º
الحل:
8) 1260º
الحل:
9) 1800º
الحل:
10) 4500º
الحل:
أوجد قيمة x في كل من الشكلين الآتيين:
11)
الحل:
12)
الحل:
استعمل لإيجاد كل مما يأتي:
13)
الحل:
14) WZ
الحل:
WZ = XY =24
15)
الحل:
16) إنارة: استعمل مقبض الانارة العلوي الذي يشكل متوازي أضلاع في إيجاد في .
الحل:
زاويتان متكاملتان.
جبر: أوجد قيم المتغيرات في كل من متوازيي الأضلاع الآتيين: (الدرس 2-1).
17)
الحل:
18)
الحل:
19) برهان: اكتب برهاناً ذا عمودين.
- المعطيات:
- المطلوب:
الحل:
البرهان: العبارات (المبررات):
1) متوازيا الأضلاع GFBA، HACD (معطيات).
2) (الزوايا المتقابلة في متوازي الأضلاع متطابقة).
3) (خاصية التعدي).
أوجد قيمتي x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع:
20)
الحل:
21)
الحل:
22) طاولات: لماذا يبقى سطح طاولة كي الثياب في الصورة أدناه موازياً لأرضية الغرفة دائماً؟
الحل:
عمل الساقان بحيث ينصف كل منهما الآخر اذن فالشكل الرباعي المتكون من أطراف الساقين يكون دائماً متوازي الأضلاع، لذلك فسطح الطاولة العلوي يبقى موازياً لسطح الأرض.
23) اختيار من متعدد: أي الاشكال الرباعية الآتية ليس متوازي أضلاع؟
الحل:
هندسة إحداثية: حدد ما إذا كان الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي متوازي أضلاع. برر إجابتك باستعمال الطريقة المحددة في السؤال.
24) صيغة المسافة بين نقطتين.
الحل:
نعم، يجب ان يكون كل ضلعين متقابلين متطابقين.
- المسافة بين A وB تساوي . والمسافة بين B وC تساوي
- المسافة بين C وD تساوي . والمسافة بين D وA تساوي
بما أن المسافة بين نقطتين تحسب من خلال
25) صيغة الميل.
الحل:
بما أن ميل لا يساوي مبل ,فإن QRST ليس متوازي أضلاع.
مشاركة الدرس
الاختبارات
اختبار الكتروني:اختبار منتصف الفصل
10%
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]%;" role="progressbar" aria-valuenow="
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)




النقاشات