اختبار الفصل
أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:
1) السداسي.
n=6
720°=180°.(4)=180°.(6-2)=180°.(n-2)
2) ذو 16 ضلعاً.
n=16
2520°=180°.(14)=180°.(16-2)=180°.(n-2)
3) فن: تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض
واعتقدت أنها ستمثل مربعاً.
a) كيف يمكنها التحقق من أن الإطار مربع؟
إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.
b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.
بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft
وبما أن زوايا المربع الأربعة قائمة فإن y=90°
الشكل الرباعي ABCD شبه منحرف متطابق الساقين.
4) ما الزاوية التي تطابق ؟
حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.
5) ما الضلع الذي يوازي ؟
حسب تعريف شبه المنحرف يكون:
6) ما القطعة المستقيمة التي تطابق ؟
حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.
وبالتالي فإن:
أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:
7) 900
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 900 هو حل المعادلة:
بما أن n=7 إذاً للمضلع 7 أضلاع.
8) 1890
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 1890 هو حل المعادلة:
بما أن n=13 إذاً للمضلع 13 ضلع.
9) 2880
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 2880 هو حل المعادلة:
بما أن n=18 إذاً للمضلع 18 ضلع.
10) 5400
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 5400 هو حل المعادلة:
بما أن n=32 إذاً للمضلع 32 ضلع.
11) اختيار من متعدد: إذا كان QRST متوازي الأضلاع، فما قيمة x؟
- 11
- 12
- 13
- 14
إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:
12) GF
بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.
نستعمل نظرية فيثاغورس لإيجاد GF:
13)
بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون ، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية 360:
جبر: استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:
14)
بما أن قطرا المعين متعامدان فإن المثلث قائم وبالتالي فإن:
15) إذا كان 12 = PR، فأوجد RN.
قطرا المعين ينصف كل منهما الآخر: RN=PR=12
16) إذا كان 124 = ، فأوجد .
كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:
17) إنشاءات: تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.
نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.
استعمل المبين جانباً لإيجاد كل مما يأتي:
18)
كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)
19) JK
كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)
JK=ML=6
20)
كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)
جبر: استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:
21) إذا كان ، فاوجد EG.
لإيجاد EG نوجد قيمة x:
لحساب EG نعوض قيمة x=9:
22) إذا كان ، فأوجد .
نوجد قيمة x:
نعوض قيمة x=5:
23) إذا كان ، فأوجد GF.
نوجد قيمة x:
نعوض قيمة x=10:
حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.
24) .JPG)
نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)
25) 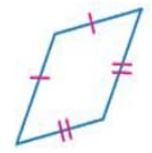
الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.
مشاركة الدرس
الاختبارات
اختبار الكتروني: اختبار الفصل
<div class="progress" style="height: 18px;"><div class="bg-success" style="width: <?= $data['percent'] ?>%;" role="progressbar" aria-valuenow="<?= $data['percent'] ?>" aria-valuemin="0" aria-valuemax="100"></div><div class="bg-danger" style="width: <?= $data['percent_w'] ?>%;" role="progressbar" aria-valuenow="<?= $data['percent_w'] ?>" aria-valuemin="0" aria-valuemax="100"></div>
$viewFile = '/home/saborah/public_html/newstyle/app/View/Elements/lesson/exams.ctp'
$dataForView = array(
'GUI' => array(
'headline' => 'اختبار الفصل',
'pagetitle' => 'اختبار الفصل',
'keywords' => null,
'description' => '',
'navigation' => array(
(int) 0 => array(
[maximum depth reached]
),
(int) 1 => array(
[maximum depth reached]
),
(int) 2 => array(
[maximum depth reached]
),
(int) 3 => array(
[maximum depth reached]
),
(int) 4 => array(
[maximum depth reached]
)
),
'layout' => 'lesson',
'menu' => array(),
'activemenu' => '0',
'pathmenu' => array()
),
'nodes_no_icon' => array(),
'nodes_icon' => array(),
'nodes_count' => (int) 0,
'files' => array(),
'node' => array(
'Nodetext' => array(
'slug' => 'اختبار_الفصل',
'title' => 'اختبار الفصل',
'title_seo' => null,
'content' => '<h2><img alt="اختبار الفصل" src="https://saborah.net/app/webroot/upload/images/images/1(2321).JPG" /></h2>
<h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> السداسي.</h2>
<p>n=6</p>
<p>720°=180°.(4)=180°.(6-2)=180°.(n-2)</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> ذو 16 ضلعاً.</h2>
<p>n=16</p>
<p>2520°=180°.(14)=180°.(16-2)=180°.(n-2)</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> <span style="color:#e74c3c;">فن:</span> تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض<br />
واعتقدت أنها ستمثل مربعاً.</h2>
<h2>a) كيف يمكنها التحقق من أن الإطار مربع؟</h2>
<p>إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.</p>
<h2>b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.</h2>
<p><img alt="مربع" src="https://saborah.net/app/webroot/upload/images/images/1(5969).JPG" /></p>
<p>بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft</p>
<p>وبما أن زوايا المربع الأربعة قائمة فإن y=90°</p>
<h2>الشكل الرباعي ABCD شبه منحرف متطابق الساقين.</h2>
<h2>4) ما الزاوية التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>C</mi></math>؟</h2>
<p>حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>D</mi><mo>≅</mo><mo>∠</mo><mi>C</mi></math></p>
<h2>5) ما الضلع الذي يوازي <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover></math>؟</h2>
<p>حسب تعريف شبه المنحرف يكون: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover><mo>‖</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo>¯</mo></mover></math></p>
<h2>6) ما القطعة المستقيمة التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover></math>؟</h2>
<p>حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.</p>
<p>وبالتالي فإن: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover><mo>≅</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>¯</mo></mover></math></p>
<h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:</h2>
<h2>7) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>1260</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=7 إذاً للمضلع 7 أضلاع.</p>
<h2>8) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>2340</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>13</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=13 إذاً للمضلع 13 ضلع.</p>
<h2>9) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>3240</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>18</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=18 إذاً للمضلع 18 ضلع.</p>
<h2>10) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>5760</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>32</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=32 إذاً للمضلع 32 ضلع.</p>
<h2>11) <span style="color:#e74c3c;">اختيار من متعدد:</span> إذا كان QRST متوازي الأضلاع، فما قيمة x؟</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6108).JPG" /></p>
<ul>
<li>11</li>
<li>12</li>
<li><span style="color:#27ae60;"><u><strong>13</strong></u></span></li>
<li>14</li>
</ul>
<h2>إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:</h2>
<h2>12) GF</h2>
<p><img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1.JPG" /></p>
<p>بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.</p>
<p>نستعمل نظرية فيثاغورس لإيجاد GF:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mo>(</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>16</mn><mo>+</mo><mn>9</mn></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>25</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>G</mi><mi>F</mi><mo>=</mo><msqrt><mn>25</mn></msqrt><mo>=</mo><mn>5</mn><mo> </mo><mi>للطرفين</mi><mo> </mo><mi>الموجب</mi><mo> </mo><mi>التربيعي</mi><mo> </mo><mi>الجذر</mi><mo> </mo><mi>بأخذ</mi></mtd></mtr></mtable></math></p>
<h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi></math></h2>
<p><img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(2).JPG" /></p>
<p>بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi mathvariant="normal">∠</mi><mi>G</mi></math>، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>360:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">∠</mi><mi>C</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>F</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>G</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>67</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><msup><mn>49</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi>N</mi></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>67</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>49</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>244</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2><span style="color:#e74c3c;">جبر:</span> استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6110).JPG" /></p>
<h2>14) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi></math></h2>
<p>بما أن قطرا المعين متعامدان فإن المثلث <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">△</mi><mi>M</mi><mi>R</mi><mi>N</mi></math> قائم وبالتالي فإن:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi><mo>=</mo><msup><mn>90</mn><mo>∘</mo></msup></math></p>
<h2>15) إذا كان 12 = PR، فأوجد RN.</h2>
<p>قطرا المعين ينصف كل منهما الآخر: RN=PR=12</p>
<h2>16) إذا كان <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>124 = <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi></math>.</h2>
<p>كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi><mo>=</mo><mfrac><mrow><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></mrow><mn>2</mn></mfrac><mo>=</mo><mfrac><msup><mn>124</mn><mo>∘</mo></msup><mn>2</mn></mfrac><mo>=</mo><msup><mn>62</mn><mo>∘</mo></msup></math></p>
<h2>17) <span style="color:#e74c3c;">إنشاءات:</span> تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.</h2>
<p>نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.</p>
<h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>◻</mi><mi>J</mi><mi>K</mi><mi>L</mi><mi>M</mi></math> المبين جانباً لإيجاد كل مما يأتي:</h2>
<p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(3).JPG" /></p>
<h2>18) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi></math></h2>
<p>كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>109</mn><mo>∘</mo></msup></math></p>
<h2>19) JK</h2>
<p>كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)</p>
<p>JK=ML=6</p>
<h2>20) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi></math></h2>
<p>كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2><span style="color:#e74c3c;">جبر:</span> استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:</h2>
<p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(4).JPG" /></p>
<h2>21) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>F</mi><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn><mo>,</mo><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></math>، فاوجد EG.</h2>
<p>لإيجاد EG نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mover><mrow><mi>E</mi><mi>G</mi></mrow><mo accent="false">¯</mo></mover></mtd><mtd><mo>≅</mo><mover><mrow><mi>D</mi><mi>F</mi></mrow><mo accent="false">¯</mo></mover></mtd></mtr><mtr><mtd><mi>E</mi><mi>G</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>F</mi></mtd></mtr><mtr><mtd><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></mtd><mtd><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p>
<p>لحساب EG نعوض قيمة x=9:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>3</mn><mo>(</mo><mn>9</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>21</mn></math></p>
<h2>22) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>,</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi><mo>=</mo><mo>(</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn><msup><mo>)</mo><mo>∘</mo></msup></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></math>.</h2>
<p>نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn></mtd><mtd><mo>=</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>7</mn><mo>+</mo><mn>3</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p>
<p>نعوض قيمة x=5:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><mo>(</mo><mn>5</mn><mo>(</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><msup><mn>22</mn><mo>∘</mo></msup></math></p>
<h2>23) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>E</mi><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi><mo>,</mo><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></math>، فأوجد GF.</h2>
<p>نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>G</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>E</mi></mtd></mtr><mtr><mtd><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>20</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr></mtable></math></p>
<p>نعوض قيمة x=10:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mo>(</mo><mn>10</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>40</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>34</mn></math></p>
<h2>حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.</h2>
<h2>24) <img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(5).JPG" /></h2>
<p>نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)</p>
<h2>25) <img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 2.JPG" /></h2>
<p>الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '7877',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
),
'children' => array(
(int) 0 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 1 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 2 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 3 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 4 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 5 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 6 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 7 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 8 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 9 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
),
(int) 10 => array(
'Nodetext' => array(
[maximum depth reached]
),
'Node' => array(
[maximum depth reached]
)
)
),
'exams' => array(
(int) 0 => array(
'id' => '1621',
'title' => 'اختبار الكتروني: اختبار الفصل',
'questions' => null,
'percent' => (float) NAN
)
),
'videos' => array(
(int) 0 => array(
'Nodegallery' => array(
[maximum depth reached]
),
'Nodegallerytext' => array(
[maximum depth reached]
)
),
(int) 1 => array(
'Nodegallery' => array(
[maximum depth reached]
),
'Nodegallerytext' => array(
[maximum depth reached]
)
),
(int) 2 => array(
'Nodegallery' => array(
[maximum depth reached]
),
'Nodegallerytext' => array(
[maximum depth reached]
)
)
),
'comments' => array(),
'news' => array(
(int) 0 => array(
'Item' => array(
[maximum depth reached]
),
'Itemtext' => array(
[maximum depth reached]
)
),
(int) 1 => array(
'Item' => array(
[maximum depth reached]
),
'Itemtext' => array(
[maximum depth reached]
)
),
(int) 2 => array(
'Item' => array(
[maximum depth reached]
),
'Itemtext' => array(
[maximum depth reached]
)
)
),
'BANNERS' => array(
'home-classes-up' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'home-classes-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'articles-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'lesson-up' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'level-up' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'lesson-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array(
[maximum depth reached]
)
),
'level-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'related-lessons' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'article-up' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'article-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'question-up' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'question-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
),
'question-lesson-down' => array(
'Zone' => array(
[maximum depth reached]
),
'Banner' => array([maximum depth reached])
)
),
'_privilege' => array(),
'_menus' => array(),
'_nodes' => array(),
'_contactus' => array(),
'_banners' => array(),
'_pages' => array(),
'_langs' => array(
(int) 0 => array(
'Lang' => array(
[maximum depth reached]
)
)
),
'request_count' => (int) 998,
'socical_networks' => array(
(int) 0 => array(
'Confdb' => array(
[maximum depth reached]
)
),
(int) 1 => array(
'Confdb' => array(
[maximum depth reached]
)
),
(int) 2 => array(
'Confdb' => array(
[maximum depth reached]
)
)
),
'_Language' => array(
'ara' => 'Arabic'
),
'Config' => array(
'name_eng' => 'Saborah',
'name_ara' => 'موقع سبورة - طلاب السعودية',
'from' => 'سبورة',
'fromaddress' => 'noreply@saborah.net',
'email_monitor' => 'info@saborah.net',
'listrow' => '12',
'url' => 'https://saborah.net',
'email_formname' => 'سبورة',
'facebook' => '',
'twitter' => '#',
'youtube' => '#',
'linkedin' => '#',
'phone' => '',
'time_format' => 'H:i A',
'node_sep_slug' => '_',
'latest_update_website' => '2022-12-02 14:25:47',
'latest_login_admin' => '2022-03-16 06:26:54',
'google_secret_key' => '6LcBYhUTAAAAABPinPa4vlhvDuhne95ZnfUao0tw',
'site_key' => '6LcBYhUTAAAAAIurIcmwQzN4C2kkYLYBHyGxKWzO',
'map' => '31.99415,35.870693',
'map_center' => '31.99415,35.870693',
'keywords_ara' => 'حلول, حل, إجابات, إجابة, علوم, رياضيات, فقه, لغة, عربية, متوسط, ثانوي, الفصل, الأول, الثاني, مواد, دراسة, واجبي',
'description_ara' => 'حل الواجبات المدرسية لطلاب السعودية ف1 ف2 وجميع المواد والصفوف الدراسية من رياضيات وعلوم واجتماعيات وفقه وحاسوب',
'instagram' => '',
'admin_email' => 'mkhuder@gmail.com',
'map_zoom' => '14',
'header_code' => '<!-- Google tag (gtag.js) -->
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-216508974-1"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-216508974-1');
</script>
<!--
<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>
-->
<link rel="manifest" href="/manifest.json" > <script> const appId = "95217417-b5c7-42eb-ada0-f01acc0ba857"; const auto_register = true; //write your tags as json format //const tags = '{"key1":"value1", "key2":"value2"}'; </script> <script src="https://pushtiger.com/settings.js" ></script>',
'body_code' => '',
'website_author' => 'Sama IT Solution',
'dashboard_url' => '/admin/node/index',
'admin-panel-url' => 'backdoor',
'admin-theme-color' => '3994C7',
'email_format' => '[^@]+@[^@]+.[a-zA-Z]{2,6}',
'password_format' => '.{6,}',
'keywords_eng' => '',
'description_eng' => '',
'google-map-api-key' => 'AIzaSyBb71HgSD8EiowFnx3HRBa5pw96ChhJeMU',
'max-char-node-url' => '58',
'default-color' => '1075a9',
'api-key' => '317bbb',
'apiKey' => 'AIzaSyDQGQ05rKO5otB4_EqLW-oboBIgdDLBAUQ',
'authDomain' => 'saborah-f5614.firebaseapp.com',
'databaseURL' => 'https://saborah-f5614-default-rtdb.europe-west1.firebasedatabase.app',
'user-offline-after' => '1',
'service_account' => 'saborah-f5614-b95c91e5ec9f.json',
'thumb_width' => '400',
'min-nodes-count-view-news' => '4',
'name_default_ara' => 'سبورة',
'google-api-notification-key' => 'AAAAP5FT_i8:APA91bGmsp2e-BgVYKUO58Su2zlMp3qX6aynA4flPYpjjYEOrMD1A7zeRuC4YxVg254PcbFquFOdHKOAm5WKPyQh2wzwBVe_3HB9TSxoRokeGD21LWD4Q3wj8WShkGcEsx6iFQkqehlM',
'app-package-names' => 'net.saborah.app,net.saborah.app.fifth,net.saborah.app.sixth,net.saborah.app.seventh,net.saborah.app.eighth,net.saborah.app.ninth,net.saborah.app.thanwya,net.saborah.app.third,net.saborah.app.fourth',
'user-new-type' => '100',
'user-active-type' => '200',
'user-special-type' => '300',
'header_code_inside' => '<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>',
'google-play-app' => 'https://play.google.com/store/apps/details?id=net.saborah.app',
'header_code_inside_question' => ' <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>',
'Languages' => null
),
'headline' => 'الاختبارات'
)
$GUI = array(
'headline' => 'اختبار الفصل',
'pagetitle' => 'اختبار الفصل',
'keywords' => null,
'description' => '',
'navigation' => array(
(int) 0 => array(
'name' => 'الثانوية مقررات',
'url' => '/lesson/39/الثانوية_مقررات'
),
(int) 1 => array(
'name' => 'المسار المشترك',
'url' => '/lesson/470/المسار_المشترك'
),
(int) 2 => array(
'name' => 'الرياضيات 2',
'url' => '/lesson/471/الرياضيات_2'
),
(int) 3 => array(
'name' => 'الفصل الأول: الأشكال الرباعية',
'url' => '/lesson/472/الفصل_الأول_الأشكال_الرباعية'
),
(int) 4 => array(
'name' => 'اختبار الفصل',
'url' => '/lesson/7877/اختبار_الفصل'
)
),
'layout' => 'lesson',
'menu' => array(),
'activemenu' => '0',
'pathmenu' => array()
)
$nodes_no_icon = array()
$nodes_icon = array()
$nodes_count = (int) 0
$files = array()
$node = array(
'Nodetext' => array(
'slug' => 'اختبار_الفصل',
'title' => 'اختبار الفصل',
'title_seo' => null,
'content' => '<h2><img alt="اختبار الفصل" src="https://saborah.net/app/webroot/upload/images/images/1(2321).JPG" /></h2>
<h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> السداسي.</h2>
<p>n=6</p>
<p>720°=180°.(4)=180°.(6-2)=180°.(n-2)</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> ذو 16 ضلعاً.</h2>
<p>n=16</p>
<p>2520°=180°.(14)=180°.(16-2)=180°.(n-2)</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> <span style="color:#e74c3c;">فن:</span> تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض<br />
واعتقدت أنها ستمثل مربعاً.</h2>
<h2>a) كيف يمكنها التحقق من أن الإطار مربع؟</h2>
<p>إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.</p>
<h2>b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.</h2>
<p><img alt="مربع" src="https://saborah.net/app/webroot/upload/images/images/1(5969).JPG" /></p>
<p>بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft</p>
<p>وبما أن زوايا المربع الأربعة قائمة فإن y=90°</p>
<h2>الشكل الرباعي ABCD شبه منحرف متطابق الساقين.</h2>
<h2>4) ما الزاوية التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>C</mi></math>؟</h2>
<p>حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>D</mi><mo>≅</mo><mo>∠</mo><mi>C</mi></math></p>
<h2>5) ما الضلع الذي يوازي <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover></math>؟</h2>
<p>حسب تعريف شبه المنحرف يكون: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover><mo>‖</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo>¯</mo></mover></math></p>
<h2>6) ما القطعة المستقيمة التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover></math>؟</h2>
<p>حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.</p>
<p>وبالتالي فإن: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover><mo>≅</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>¯</mo></mover></math></p>
<h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:</h2>
<h2>7) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>1260</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=7 إذاً للمضلع 7 أضلاع.</p>
<h2>8) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>2340</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>13</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=13 إذاً للمضلع 13 ضلع.</p>
<h2>9) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>3240</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>18</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=18 إذاً للمضلع 18 ضلع.</p>
<h2>10) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400</h2>
<p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400 هو حل المعادلة:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>5760</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>32</mn></mtd></mtr></mtable></math></p>
<p>بما أن n=32 إذاً للمضلع 32 ضلع.</p>
<h2>11) <span style="color:#e74c3c;">اختيار من متعدد:</span> إذا كان QRST متوازي الأضلاع، فما قيمة x؟</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6108).JPG" /></p>
<ul>
<li>11</li>
<li>12</li>
<li><span style="color:#27ae60;"><u><strong>13</strong></u></span></li>
<li>14</li>
</ul>
<h2>إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:</h2>
<h2>12) GF</h2>
<p><img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1.JPG" /></p>
<p>بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.</p>
<p>نستعمل نظرية فيثاغورس لإيجاد GF:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mo>(</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>16</mn><mo>+</mo><mn>9</mn></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>25</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>G</mi><mi>F</mi><mo>=</mo><msqrt><mn>25</mn></msqrt><mo>=</mo><mn>5</mn><mo> </mo><mi>للطرفين</mi><mo> </mo><mi>الموجب</mi><mo> </mo><mi>التربيعي</mi><mo> </mo><mi>الجذر</mi><mo> </mo><mi>بأخذ</mi></mtd></mtr></mtable></math></p>
<h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi></math></h2>
<p><img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(2).JPG" /></p>
<p>بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi mathvariant="normal">∠</mi><mi>G</mi></math>، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>360:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">∠</mi><mi>C</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>F</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>G</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>67</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><msup><mn>49</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi>N</mi></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>67</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>49</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>244</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2><span style="color:#e74c3c;">جبر:</span> استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6110).JPG" /></p>
<h2>14) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi></math></h2>
<p>بما أن قطرا المعين متعامدان فإن المثلث <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">△</mi><mi>M</mi><mi>R</mi><mi>N</mi></math> قائم وبالتالي فإن:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi><mo>=</mo><msup><mn>90</mn><mo>∘</mo></msup></math></p>
<h2>15) إذا كان 12 = PR، فأوجد RN.</h2>
<p>قطرا المعين ينصف كل منهما الآخر: RN=PR=12</p>
<h2>16) إذا كان <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>124 = <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi></math>.</h2>
<p>كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi><mo>=</mo><mfrac><mrow><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></mrow><mn>2</mn></mfrac><mo>=</mo><mfrac><msup><mn>124</mn><mo>∘</mo></msup><mn>2</mn></mfrac><mo>=</mo><msup><mn>62</mn><mo>∘</mo></msup></math></p>
<h2>17) <span style="color:#e74c3c;">إنشاءات:</span> تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.</h2>
<p>نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.</p>
<h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>◻</mi><mi>J</mi><mi>K</mi><mi>L</mi><mi>M</mi></math> المبين جانباً لإيجاد كل مما يأتي:</h2>
<p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(3).JPG" /></p>
<h2>18) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi></math></h2>
<p>كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>109</mn><mo>∘</mo></msup></math></p>
<h2>19) JK</h2>
<p>كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)</p>
<p>JK=ML=6</p>
<h2>20) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi></math></h2>
<p>كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2><span style="color:#e74c3c;">جبر:</span> استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:</h2>
<p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(4).JPG" /></p>
<h2>21) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>F</mi><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn><mo>,</mo><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></math>، فاوجد EG.</h2>
<p>لإيجاد EG نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mover><mrow><mi>E</mi><mi>G</mi></mrow><mo accent="false">¯</mo></mover></mtd><mtd><mo>≅</mo><mover><mrow><mi>D</mi><mi>F</mi></mrow><mo accent="false">¯</mo></mover></mtd></mtr><mtr><mtd><mi>E</mi><mi>G</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>F</mi></mtd></mtr><mtr><mtd><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></mtd><mtd><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p>
<p>لحساب EG نعوض قيمة x=9:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>3</mn><mo>(</mo><mn>9</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>21</mn></math></p>
<h2>22) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>,</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi><mo>=</mo><mo>(</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn><msup><mo>)</mo><mo>∘</mo></msup></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></math>.</h2>
<p>نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn></mtd><mtd><mo>=</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>7</mn><mo>+</mo><mn>3</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p>
<p>نعوض قيمة x=5:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><mo>(</mo><mn>5</mn><mo>(</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><msup><mn>22</mn><mo>∘</mo></msup></math></p>
<h2>23) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>E</mi><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi><mo>,</mo><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></math>، فأوجد GF.</h2>
<p>نوجد قيمة x:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>G</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>E</mi></mtd></mtr><mtr><mtd><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>20</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr></mtable></math></p>
<p>نعوض قيمة x=10:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mo>(</mo><mn>10</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>40</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>34</mn></math></p>
<h2>حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.</h2>
<h2>24) <img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(5).JPG" /></h2>
<p>نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)</p>
<h2>25) <img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 2.JPG" /></h2>
<p>الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '7877',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
)
$children = array(
(int) 0 => array(
'Nodetext' => array(
'slug' => 'التهيئة_للفصل_الأول',
'title' => 'التهيئة للفصل الأول',
'title_seo' => null,
'content' => '<p><img alt="التهيئة للفصل الاول" src="https://saborah.net/app/webroot/upload/images/images/التهيئة للفصل الأول.JPG" /></p>
<h2>أجب عن الاختبار الآتي انظر المراجعة السريعة قبل الإجابة عن الاختبار.</h2>
<h2><img alt="اختبار سريع" src="https://saborah.net/app/webroot/upload/images/images/Capture(1).JPG" /><br />
أوجد قيم x,y في كل مما يأتي مقرباً إلى أقرب عشر:</h2>
<h2>1)</h2>
<p><img alt="مثلث 1" src="https://saborah.net/app/webroot/upload/images/images/مثلث 1.JPG" /></p>
<p><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></p>
<p>الزاوية الخارجية عن المثلث = مجموع الزاويتين الداخليتين البعيدتين.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>4</mn><mi>x</mi><mo>=</mo><mn>83</mn><mo>+</mo><mi>x</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mi>x</mi><mo>=</mo><mn>83</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>=</mo><mn>83</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>27.7</mn></mtd></mtr></mtable></math></p>
<h2>2)</h2>
<p><img alt="مثلث 2" src="https://saborah.net/app/webroot/upload/images/images/مثلث 2.JPG" /></p>
<p><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></p>
<p>بما أن المثلث جميع أضلاعه متطابقة إذاً:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="0em"><mtr><mtd><mn>9</mn><mi>x</mi><mo>=</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>4</mn><mi>x</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>1</mn></mtd></mtr></mtable></math></p>
<p>بما أن المثلث جميع أضلاعه متطابقة إذاً: جميع زواياه متطابقة و = <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>60</mn><mo>°</mo></math>.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo> </mo><mo>=</mo><mo> </mo><mn>180</mn><mo> </mo><mo>-</mo><mn>60</mn><mspace linebreak="newline"></mspace><mi>y</mi><mo> </mo><mo>=</mo><mo> </mo><mn>120</mn><mo>°</mo></math></p>
<h2>3) <span style="color:#e74c3c;">مدن:</span> تمثل مواقع كل من الرياض وجدة وأبها رؤوس مثلث كما في الشكل أدناه إذا كان محيط هذا المثلث 2198km فأوجد المسافة الجوية بين كل من المدن الثلاث.</h2>
<h2><img alt="مثلث 3" src="https://saborah.net/app/webroot/upload/images/images/مثلث 3.JPG" /></h2>
<h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2>
<p>محيط المثلث = مجموع أطوال أضلاعه.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>=</mo><mo> </mo><mfenced><mrow><mn>53</mn><mo>.</mo><mn>4</mn><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>80</mn><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>90</mn><mo> </mo><mo>+</mo><mo> </mo><mn>88</mn><mo>.</mo><mn>5</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>2198</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mfenced><mrow><mn>221</mn><mo>.</mo><mn>9</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>90</mn><mo> </mo><mo>-</mo><mo> </mo><mn>2198</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mfenced><mrow><mn>221</mn><mo>.</mo><mn>9</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>2108</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mi>x</mi><mo> </mo><mo>=</mo><mo> </mo><mn>9</mn><mo>.</mo><mn>5</mn></math></p>
<ul>
<li>المسافة بين الرياض وجدة = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mn>90</mn><mo> </mo><mo>+</mo><mo> </mo><mi mathvariant="normal">x</mi><mn>80</mn><mo> </mo><mo>=</mo><mo> </mo><mn>90</mn><mo> </mo><mo>+</mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>80</mn><mo> </mo><mo>=</mo><mn>850</mn></math>.</li>
<li>المسافة بين الرياض وأبها = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mn>5</mn><mo>.</mo><mn>88</mn><mo> </mo><mo>=</mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>5</mn><mo>.</mo><mn>88</mn><mo> </mo><mo>=</mo><mo> </mo><mn>8</mn><mo>.</mo><mn>840</mn></math>.</li>
<li>المسافة بين جدة وأبها = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mn>4</mn><mo>.</mo><mn>53</mn><mo> </mo><mo>=</mo><mo> </mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>4</mn><mo>.</mo><mn>53</mn><mo> </mo><mo>=</mo><mo> </mo><mn>3</mn><mo>.</mo><mn>507</mn></math>.</li>
</ul>
<h2>حدد ما إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> متوازيين أو متعامدين أو غير ذلك في كل مما يأتي:</h2>
<h2 style="direction: ltr; text-align: right;">.A(3,3),B(8,2),C(6, -1),D(1,0) (4</h2>
<h2 style="direction: ltr; text-align: right;"><span style="color:#c0392b;">:الحل</span></h2>
<h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>−</mo><mn>3</mn></mrow><mrow><mn>8</mn><mo>−</mo><mn>3</mn></mrow></mfrac><mo> </mo><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>AB</mi><mo> </mo></mrow><mo>→</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>1</mn><mrow><mo>−</mo><mn>5</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>0</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>1</mn><mo>−</mo><mn>6</mn></mrow></mfrac><mo> </mo><mo>:</mo><mover accent="true"><mrow><mo> </mo><mi>CD</mi></mrow><mo>↔</mo></mover><mtext> ميل  </mtext></mtd></mtr></mtable></math></h2>
<p style="direction: ltr; text-align: right;">.بما أن ميل كل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> متساويين إذاً فهما متوازيين</p>
<h2 style="direction: ltr; text-align: right;">.A(4,2),B(1,-3),C(-3,5),D(2,2) (5</h2>
<h2 style="direction: ltr; text-align: right;"><font color="#c0392b"><span style="font-size: 16px;"><b>:الحل</b></span></font></h2>
<h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>5</mn><mn>3</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn></mrow><mrow><mo>−</mo><mn>3</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>2</mn></mrow><mrow><mn>1</mn><mo>−</mo><mn>4</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>AB</mi><mo> </mo></mrow><mo>↔</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>3</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>−</mo><mn>5</mn></mrow><mrow><mn>2</mn><mo>−</mo><mo>(</mo><mo>−</mo><mn>3</mn><mo>)</mo></mrow></mfrac><mo> </mo><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>CD</mi><mo> </mo></mrow><mo>↔</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr></mtable></math></h2>
<p style="direction: ltr; text-align: right;">.بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> حاصل ضربهم = -1 إذاً فهما متعامدان</p>
<h2 style="direction: ltr; text-align: right;">.A(-8,-7),B(4,-4),C(-2,-5),D(1,7) (6</h2>
<h2 style="direction: ltr; text-align: right;"><span style="color:#c0392b;">:الحل</span></h2>
<h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi>m</mi><mo>=</mo><mfrac><mrow><msub><mi>y</mi><mn>2</mn></msub><mo>−</mo><msub><mi>y</mi><mn>1</mn></msub></mrow><mrow><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>1</mn><mn>4</mn></mfrac><mo>=</mo><mfrac><mn>3</mn><mn>12</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>4</mn><mo>+</mo><mn>7</mn></mrow><mrow><mn>4</mn><mo>+</mo><mn>8</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mrow><mi>A</mi><mi>B</mi><mo> </mo></mrow><mo>↔</mo></mover><mtext> ميل  </mtext></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mo>=</mo><mfrac><mn>12</mn><mn>3</mn></mfrac><mo>=</mo><mfrac><mrow><mn>7</mn><mo>+</mo><mn>5</mn></mrow><mrow><mn>1</mn><mo>+</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mrow><mi>C</mi><mi>D</mi><mo> </mo></mrow><mo>↔</mo></mover><mtext>ميل</mtext></mtd></mtr></mtable></math></h2>
<p style="direction: ltr; text-align: right;">.بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> غير متساويين فهما غير متوازيين وليس حاصل ضربهم =-1 إذا فهمت غير ذلك</p>
<h2>7) <span style="color:#e74c3c;">حدائق:</span> صمم مهندس رسماً لحديقة رباعية الشكل إحداثيات رؤوسها: A(-2,1),B(3,-3),C(5,7),D(-3 ,4) إذا رسم ممرين يقطعانها <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>↔</mo></mover></math>, فهل الممران متعامدان؟ فسر اجابتك.</h2>
<h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2>
<h2><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>7</mn></mrow><mn>6</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>4</mn></mrow><mrow><mn>3</mn><mo>+</mo><mn>3</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mi>BD</mi><mo>↔</mo></mover><mo> </mo><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>6</mn><mn>7</mn></mfrac><mo>=</mo><mfrac><mrow><mn>7</mn><mo>−</mo><mn>1</mn></mrow><mrow><mn>5</mn><mo>+</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mi>AC</mi><mo>↔</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr></mtable></math></h2>
<p>بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi><mi>ِ</mi><mi>ِ</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>↔</mo></mover></math> حاصل ضربهم = -1 إذاً فهما متعامدان.</p>
<h2>أوجد المسافة بين كل نقطتين ثم أوجد احداثيات نقطة منتصف القطعة الواصلة بينهما في كل مما يأتي:</h2>
<h2 style="direction: ltr; text-align: right;">.J(-6,2),K(-1,3) (8</h2>
<h2 style="direction: ltr; text-align: right;"><strong><span style="color:#c0392b;"><span style="font-size:16px;">:الحل</span></span></strong></h2>
<h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>26</mn></msqrt></mtd></mtr></mtable></math></h2>
<h2 style="direction: ltr; text-align: right;">.R(2,5),S(8,4) (9</h2>
<h2 style="direction: ltr; text-align: right;"><strong><span style="color:#c0392b;"><span style="font-size:16px;">:الحل</span></span></strong></h2>
<h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">8</mn><mo>−</mo><mn mathvariant="bold">2</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">4</mn><mo>−</mo><mn mathvariant="bold">5</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn mathvariant="bold">1</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>37</mn></msqrt></mtd></mtr></mtable></math></h2>
<h2>10) <span style="color:#e74c3c;">مسافات:</span> وقف شخص على النقطة (20,80)T من مستوى احداثي ورغب في الانتقال الى كل من (60,20)U و(85,110)V فما أقصر مسافة يمكن أن يقطعها الشخص؟ فسر اجابتك.</h2>
<h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2>
<h2><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">20</mn><mo>−</mo><mn mathvariant="bold">80</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">60</mn><mo>−</mo><mn mathvariant="bold">20</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn mathvariant="bold">60</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">40</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><mn>20</mn><msqrt><mn>13</mn></msqrt><mo>=</mo><mn>72.11</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">110</mn><mo>−</mo><mn mathvariant="bold">80</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">85</mn><mo>−</mo><mn mathvariant="bold">20</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">30</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">65</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><mn mathvariant="bold">5</mn><msqrt><mn mathvariant="bold">205</mn></msqrt><mo>=</mo><mn>71.6</mn></mtd></mtr></mtable></math></h2>
<p>أقصر مسافة يقطعها الشخص هي من النقطة T إلى U >.</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '490',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
),
(int) 1 => array(
'Nodetext' => array(
'slug' => 'الدرس_الأول_زوايا_المضلع',
'title' => 'الدرس الأول: زوايا المضلع',
'title_seo' => 'حل درس زوايا المضلع - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '526',
'thumb' => null,
'parentID' => '472',
'sequence' => '1',
'has_videos' => '1'
)
),
(int) 2 => array(
'Nodetext' => array(
'slug' => 'الدرس_الثاني_متوازي_الأضلاع',
'title' => 'الدرس الثاني: متوازي الأضلاع',
'title_seo' => 'حل درس متوازي الأضلاع - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '617',
'thumb' => null,
'parentID' => '472',
'sequence' => '2',
'has_videos' => '1'
)
),
(int) 3 => array(
'Nodetext' => array(
'slug' => 'الدرس_الثالث_تمييز_متوازي_الأضلاع',
'title' => 'الدرس الثالث: تمييز متوازي الأضلاع',
'title_seo' => 'حل درس تمييز متوازي الأضلاع - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '679',
'thumb' => null,
'parentID' => '472',
'sequence' => '3',
'has_videos' => '1'
)
),
(int) 4 => array(
'Nodetext' => array(
'slug' => 'اختبار_منتصف_الفصل',
'title' => 'اختبار منتصف الفصل',
'title_seo' => null,
'content' => '<p><img alt="حل اخبار منصف" src="https://saborah.net/app/webroot/upload/images/images/عناون اختبار.JPG" /></p>
<h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعات المحدبة الآتية: (الدرس 1-1).</h2>
<h2>1) الخماسي:</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>5</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>540</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>2) السباعي:</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>7</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>7</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>3) ذو 18 ضلعاً:</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>18</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>18</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>4) ذو 23 ضلعاً:</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>23</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>23</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>3780</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>أوجد قياسات جميع الزوايا في كل من المضلعين الآتيين: (الدرس 1-1).</h2>
<h2>5)</h2>
<p><img alt="شكل 5" src="https://saborah.net/app/webroot/upload/images/images/5(11).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>26</mn><mo>+</mo><mi>x</mi><mo>+</mo><mi>x</mi><mo>+</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>18</mn><mo>)</mo><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>8</mn><mi>x</mi><mo>−</mo><mn>8</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>46</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>A</mi><mo>=</mo><mn>4</mn><mo>×</mo><mn>46</mn><mo>−</mo><mn>26</mn><mo>=</mo><msup><mn>158</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>C</mi><mo>=</mo><mn>2</mn><mo>×</mo><mn>46</mn><mo>+</mo><mn>18</mn><mo>=</mo><msup><mn>110</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>B</mi><mo>=</mo><msup><mn>46</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>46</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>6)</h2>
<p><img alt="شكل 6" src="https://saborah.net/app/webroot/upload/images/images/6(9).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>16</mn><mo>+</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>+</mo><mi mathvariant="normal">x</mi><mo>+</mo><mi mathvariant="normal">x</mi><mo>+</mo><mn>10</mn><mo>)</mo><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>6</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">x</mi><mo>=</mo><mn>61</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">Q</mi><mo>=</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>16</mn><mo>=</mo><mn>2</mn><mo>×</mo><mn>61</mn><mo>−</mo><mn>16</mn><mo>=</mo><msup><mn>106</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">R</mi><mo>=</mo><mn>2</mn><mo>×</mo><mn>61</mn><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">P</mi><mo>=</mo><msup><mn>61</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">S</mi><mo>=</mo><mi mathvariant="normal">x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mn>61</mn><mo>+</mo><mn>10</mn><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه الداخلية في كل مما يأتي:</h2>
<h2>7) 720º</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>720</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>720</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>720</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>6</mn></mtd></mtr></mtable></math></p>
<h2>8) 1260º</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>1260</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1260</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1260</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p>
<h2>9) 1800º</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>1800</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1800</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1800</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>12</mn></mtd></mtr></mtable></math></p>
<h2>10) 4500º</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>4500</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4500</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4500</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>27</mn></mtd></mtr></mtable></math></p>
<h2>أوجد قيمة x في كل من الشكلين الآتيين:</h2>
<h2>11)</h2>
<p><img alt="شكل 11" src="https://saborah.net/app/webroot/upload/images/images/11(9).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mi>x</mi><mo>+</mo><mn>15</mn><mo>)</mo><mo>+</mo><mn>106</mn><mo>+</mo><mo>(</mo><mi>x</mi><mo>−</mo><mn>10</mn><mo>)</mo><mo>+</mo><mo>(</mo><mn>2</mn><mi>x</mi><mo>−</mo><mn>35</mn><mo>)</mo><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>+</mo><mn>76</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>71</mn></mtd></mtr></mtable></math></p>
<h2>12)</h2>
<p><img alt="شكل 12" src="https://saborah.net/app/webroot/upload/images/images/12(9).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mi>x</mi><mo>+</mo><mn>4</mn><mo>)</mo><mo>+</mo><mn>56</mn><mo>+</mo><mo>(</mo><mi>x</mi><mo>+</mo><mn>10</mn><mo>)</mo><mo>+</mo><mo>(</mo><mi>x</mi><mo>−</mo><mn>6</mn><mo>)</mo><mo>+</mo><mi>x</mi><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>+</mo><mn>64</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>74</mn></mtd></mtr></mtable></math></p>
<h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>W</mi><mi>X</mi><mi>Y</mi><mi>Z</mi></math> لإيجاد كل مما يأتي:</h2>
<h2><img alt="شكل 13" src="https://saborah.net/app/webroot/upload/images/images/13(7).JPG" /></h2>
<h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>W</mi><mi>Z</mi><mi>Y</mi></math></h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><msup><mn>105</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>105</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>75</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2>14) WZ</h2>
<p>الحل:</p>
<p>WZ = XY =24</p>
<h2>15) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>X</mi><mi>Y</mi><mi>Z</mi></math></h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>X</mi><mi>Y</mi><mi>Z</mi><mo> </mo><mo>=</mo><mo> </mo><mo>∠</mo><mi>Z</mi><mi>W</mi><mi>X</mi><mo> </mo><mo>=</mo><mo> </mo><mn>105</mn><mo>°</mo></math></p>
<h2>16) <span style="color:#e74c3c;">إنارة:</span> استعمل مقبض الانارة العلوي الذي يشكل متوازي أضلاع في إيجاد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>p</mi></math> في <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>P</mi><mi>Q</mi><mi>R</mi><mi>S</mi></math>.</h2>
<p><img alt="شكل 16" src="https://saborah.net/app/webroot/upload/images/images/16(4).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>S</mi><mo> </mo><mi>و</mi><mo> </mo><mo>∠</mo><mi>P</mi></math> زاويتان متكاملتان.</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>P</mi><mo> </mo><mo>=</mo><mo> </mo><mn>180</mn><mo> </mo><mo>-</mo><mn>64</mn><mo> </mo><mo>=</mo><mn>116</mn><mo>°</mo></math></p>
<h2><span style="color:#e74c3c;">جبر:</span> أوجد قيم المتغيرات في كل من متوازيي الأضلاع الآتيين: (الدرس 2-1).</h2>
<h2>17)</h2>
<p><img alt="شكل 17" src="https://saborah.net/app/webroot/upload/images/images/17(3).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">s</mi><mo>−</mo><mn>7</mn><mo>=</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">s</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">s</mi><mo>=</mo><mn>13</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">t</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">t</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">t</mi><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p>
<h2>18)</h2>
<p><img alt="شكل 18" src="https://saborah.net/app/webroot/upload/images/images/18(3).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>3</mn><mi>f</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>2</mn><mi>f</mi><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>f</mi><mo>−</mo><mn>2</mn><mi>f</mi><mo>=</mo><mn>8</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>f</mi><mo>=</mo><mn>14</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>56</mn><mo>+</mo><mo>(</mo><mn>3</mn><mi>d</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>54</mn><mo>+</mo><mn>3</mn><mi>d</mi><mo>=</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>d</mi><mo>=</mo><mn>180</mn><mo>−</mo><mn>54</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>d</mi><mo>=</mo><mn>126</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>d</mi><mo>=</mo><mn>42</mn></mtd></mtr></mtable></math></p>
<h2>19)<span style="color:#e74c3c;"> برهان: </span>اكتب برهاناً ذا عمودين.</h2>
<ul>
<li><span style="color:#e74c3c;">المعطيات:</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>G</mi><mi>F</mi><mi>B</mi><mi>A</mi><mo> </mo><mo>,</mo><mo> </mo><mo>▱</mo><mi>H</mi><mi>A</mi><mi>C</mi><mi>D</mi></math></li>
<li><span style="color:#e74c3c;">المطلوب:</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math></li>
</ul>
<p><img alt="شكل 19" src="https://saborah.net/app/webroot/upload/images/images/19(2).JPG" /></p>
<p>الحل:</p>
<p>البرهان: العبارات (المبررات):</p>
<p>1) متوازيا الأضلاع GFBA، HACD (معطيات).</p>
<p>2) <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>A</mi><mo> </mo><mo>,</mo><mo> </mo><mo>∠</mo><mi>A</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math> (الزوايا المتقابلة في متوازي الأضلاع متطابقة).</p>
<p>3) <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math> (خاصية التعدي).</p>
<h2>أوجد قيمتي x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع:</h2>
<h2>20)</h2>
<p><img alt="شكل 20" src="https://saborah.net/app/webroot/upload/images/images/20(2).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>x</mi><mo>+</mo><mn>5</mn><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi><mo>−</mo><mi>x</mi><mo>=</mo><mn>5</mn><mo>−</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>+</mo><mn>10</mn><mo>=</mo><mn>2</mn><mi>y</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>10</mn><mo>−</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p>
<h2>21)</h2>
<p><img alt="شكل 21" src="https://saborah.net/app/webroot/upload/images/images/21(1).JPG" /></p>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>2</mn><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>y</mi><mo>+</mo><mn>6</mn><mo>=</mo><mn>6</mn><mi>y</mi><mo>−</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>6</mn><mi>y</mi><mo>−</mo><mn>4</mn><mi>y</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi>y</mi><mo>=</mo><mn>14</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p>
<h2>22)<span style="color:#e74c3c;"> طاولات: </span>لماذا يبقى سطح طاولة كي الثياب في الصورة أدناه موازياً لأرضية الغرفة دائماً؟</h2>
<p><img alt="شكل 22" src="https://saborah.net/app/webroot/upload/images/images/طاولة.JPG" /></p>
<p>الحل:</p>
<p>عمل الساقان بحيث ينصف كل منهما الآخر اذن فالشكل الرباعي المتكون من أطراف الساقين يكون دائماً متوازي الأضلاع، لذلك فسطح الطاولة العلوي يبقى موازياً لسطح الأرض.</p>
<h2>23) <span style="color:#e74c3c;">اختيار من متعدد:</span> أي الاشكال الرباعية الآتية ليس متوازي أضلاع؟</h2>
<p>الحل:</p>
<p><img alt="حل 23" src="https://saborah.net/app/webroot/upload/images/images/حل 23(1).JPG" /></p>
<h2><span style="color:#e74c3c;">هندسة إحداثية:</span> حدد ما إذا كان الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي متوازي أضلاع. برر إجابتك باستعمال الطريقة المحددة في السؤال.</h2>
<h2>24) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">A</mi><mo>(</mo><mo>-</mo><mn>6</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>5</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">B</mi><mo>(</mo><mo>-</mo><mn>1</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>4</mn><mo>)</mo><mo>,</mo><mo> </mo><mi mathvariant="normal">C</mi><mo>(</mo><mn>0</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>1</mn><mo>)</mo><mo>,</mo><mo> </mo><mi mathvariant="normal">D</mi><mo>(</mo><mo>-</mo><mn>5</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>2</mn><mo>)</mo></math> صيغة المسافة بين نقطتين.</h2>
<p>الحل:</p>
<p>نعم، يجب ان يكون كل ضلعين متقابلين متطابقين.</p>
<ul>
<li>المسافة بين A وB تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>26</mn></msqrt></math>. والمسافة بين B وC تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>10</mn></msqrt></math></li>
<li>المسافة بين C وD تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>26</mn></msqrt></math>. والمسافة بين D وA تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>10</mn></msqrt></math></li>
</ul>
<p>بما أن المسافة بين نقطتين تحسب من خلال <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></math></p>
<p> </p>
<h2>25) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">Q</mi><mo>(</mo><mo>-</mo><mn>5</mn><mo> </mo><mo>,</mo><mo> </mo><mn>2</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">R</mi><mo>(</mo><mo>-</mo><mn>3</mn><mo> </mo><mo>,</mo><mo>-</mo><mn>6</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">S</mi><mo>(</mo><mn>2</mn><mo> </mo><mo>,</mo><mo> </mo><mn>2</mn><mo>)</mo><mo> </mo><mo>,</mo><mi mathvariant="normal">T</mi><mo>(</mo><mo>-</mo><mn>1</mn><mo> </mo><mo>,</mo><mo> </mo><mn>6</mn><mo>)</mo></math> صيغة الميل.</h2>
<p>الحل:</p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>4</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn></mrow><mn>8</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn><mo>+</mo><mn>3</mn></mrow><mrow><mn>2</mn><mo>+</mo><mn>6</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>QR</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn></mrow><mrow><mo>−</mo><mn>8</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>2</mn></mrow><mrow><mo>−</mo><mn>6</mn><mo>−</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>RS</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>3</mn><mrow><mo>−</mo><mn>4</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>2</mn><mo>−</mo><mn>6</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>ST</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>4</mn><mo>+</mo><mn>1</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>OT</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr></mtable></math></p>
<p>بما أن ميل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>Q</mi><mi>R</mi></mrow><mo>¯</mo></mover></math> لا يساوي مبل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>S</mi><mi>T</mi></mrow><mo>¯</mo></mover></math> ,فإن QRST ليس متوازي أضلاع.</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '751',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
),
(int) 5 => array(
'Nodetext' => array(
'slug' => 'الدرس_الرابع_المستطيل',
'title' => 'الدرس الرابع: المستطيل',
'title_seo' => 'حل درس المستطيل - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '754',
'thumb' => null,
'parentID' => '472',
'sequence' => '4',
'has_videos' => '1'
)
),
(int) 6 => array(
'Nodetext' => array(
'slug' => 'الدرس_الخامس_المعين_والمربع',
'title' => 'الدرس الخامس: المعين والمربع',
'title_seo' => 'حل درس المعين والمربع - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '787',
'thumb' => null,
'parentID' => '472',
'sequence' => '5',
'has_videos' => '1'
)
),
(int) 7 => array(
'Nodetext' => array(
'slug' => 'الدرس_السادس_شبه_المنحرف_وشكل_الطائرة_الورقية',
'title' => 'الدرس السادس: شبه المنحرف وشكل الطائرة الورقية',
'title_seo' => 'حل درس شبه المنحرف وشكل الطائرة الورقية - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '806',
'thumb' => null,
'parentID' => '472',
'sequence' => '6',
'has_videos' => '1'
)
),
(int) 8 => array(
'Nodetext' => array(
'slug' => 'دليل_الدراسة_والمراجعة',
'title' => 'دليل الدراسة والمراجعة',
'title_seo' => 'حل اسئلة دليل الدراسة والمراجعة - رياضيات 2 ثانوي مقررات',
'content' => '',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '7708',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
),
(int) 9 => array(
'Nodetext' => array(
'slug' => 'الإعداد_للاختبارات',
'title' => 'الإعداد للاختبارات',
'title_seo' => null,
'content' => '<h2><img alt="الإعداد للإختبار" src="https://saborah.net/app/webroot/upload/images/images/1(2323).JPG" /><img alt="تمارين ومسائل" src="https://saborah.net/app/webroot/upload/images/images/تمارين ومسائل(7).JPG" /></h2>
<h2>اقرأ كل مسألة مما يأتي، وحدّد المطلوب، ثم استعمل المعطيات لحلها، وبيّن خطوات حلك:</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>R</mi><mi>S</mi></mrow><mo>¯</mo></mover></math> قطعة متوسطة لشبه المنحرف MNOP. ما طول <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>R</mi><mi>S</mi></mrow><mo>¯</mo></mover></math>؟</h2>
<p><img alt="شبه منحرف" src="https://saborah.net/app/webroot/upload/images/images/1(2324).JPG" /></p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mi>RS</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mi>MN</mi><mo>+</mo><mi>PO</mi><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mn>9</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>1</mn><mo>)</mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>10</mn><mi>x</mi><mo>+</mo><mn>3</mn><mo>+</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>7</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>)</mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>14</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>=</mo><mn>7</mn><mi>x</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>7</mn><mi>x</mi><mo>=</mo><mn>5</mn><mo>+</mo><mn>1</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>2</mn><mi>x</mi><mo>=</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>R</mi><mi>S</mi><mo>=</mo><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>1</mn><mo>=</mo><mn>26</mn></mtd></mtr></mtable></math></p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo accent="false">¯</mo></mover><mo>∥</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo accent="false">¯</mo></mover></math>، فأوجد قيمة x.</h2>
<p><img alt="متوازي الأضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2325).JPG" /></p>
<p><span style="color:#27ae60;">j=115</span></p>
<p><span style="color:#27ae60;">x+65=180</span></p>
<p><span style="color:#27ae60;">x=180-65</span></p>
<p><span style="color:#27ae60;">x=115</span></p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> استعن بالتمثيل البياني أدناه في كل من السؤالين الآتيين:</h2>
<p><img alt="التمثيل البياني" src="https://saborah.net/app/webroot/upload/images/images/1(2326).JPG" /></p>
<h2>a) هل ينصف قطرا الشكل الرباعي RSTU كل منهما الآخر؟ استعمل صيغة المسافة بين نقطتين لتتحقق من إجابتك.</h2>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em" mathcolor="#007F00"><mtr><mtd><mi mathvariant="normal">S</mi><mo>(</mo><mn>5</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi>P</mi><mo>(</mo><mn>0</mn><mo>,</mo><mo>−</mo><mn>1</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">R</mi><mo>(</mo><mo>−</mo><mn>3</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">U</mi><mo>(</mo><mo>−</mo><mn>5</mn><mo>,</mo><mo>−</mo><mn>4</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">T</mi><mo>(</mo><mo>−</mo><mn>3</mn><mo>,</mo><mo>−</mo><mn>4</mn><mo>)</mo></mtd></mtr><mtr><mtd><mi>RP</mi><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>18</mn></msqrt></mtd></mtr><mtr><mtd><mi>P</mi><mi>T</mi><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>18</mn></msqrt></mtd></mtr><mtr><mtd><mtext>PS</mtext><mo>=</mo><msqrt><mo>(</mo><mn>5</mn><mo>−</mo><mn>0</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>2</mn><mo>+</mo><mn>1</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>34</mn></msqrt></mtd></mtr><mtr><mtd><mtext>UP</mtext><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>5</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>34</mn></msqrt></mtd></mtr></mtable></math></p>
<p><span style="color:#27ae60;">بما أن <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">UP</mi><mo mathcolor="#007F00">=</mo><msqrt mathcolor="#007F00"><mn>34</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">PS</mi><mo mathcolor="#007F00">=</mo><msqrt mathcolor="#007F00"><mn>34</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">PT</mi><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">3</mn><msqrt mathcolor="#007F00"><mn>2</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">RP</mi><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">3</mn><msqrt mathcolor="#007F00"><mn>2</mn></msqrt></math>، فإن القطران ينصف كل منهما الآخر.</span></p>
<h2>b) ما نوع الشكل الرباعي RSTU؟ وضح إجابتك باستعمال خصائص هذا النوع من الأشكال الرباعية أو تعريفه.</h2>
<p>متوازي أضلاع، إذا كان قطرا شكل رباعي ينصف كل منهما الآخر فإن الشكل متوازي أضلاع.</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">4)</span></span> ما مجموع قياسات الزوايا الخارجية للثماني المنتظم؟</h2>
<p>ْ360</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '7879',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '-1'
)
),
(int) 10 => array(
'Nodetext' => array(
'slug' => 'اختبار_تراكمي',
'title' => 'اختبار تراكمي',
'title_seo' => null,
'content' => '<h2><img alt="اختبار تراكمي" src="https://saborah.net/app/webroot/upload/images/images/1(2327).JPG" /></h2>
<h2><img alt="الاختيار من متعدد" src="https://saborah.net/app/webroot/upload/images/images/1(2334).JPG" /></h2>
<h2>اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة.</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>∥</mo><mi>b</mi></math>، فأي العبارات الآتية ليست صحيحة؟</h2>
<p><img alt="اختبار تراكمي" src="https://saborah.net/app/webroot/upload/images/images/1(2328).JPG" /></p>
<ul>
<li><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi mathvariant="normal">∠</mi><mn>1</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>3</mn></mtd></mtr></mtable></math></li>
<li><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mn>4</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>7</mn></math></li>
<li><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi mathvariant="normal">∠</mi><mn>2</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>5</mn></mtd></mtr></mtable></math></li>
<li><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00" mathvariant="normal">∠</mi><mn mathcolor="#007F00">8</mn><mo mathcolor="#007F00">≅</mo><mi mathcolor="#007F00" mathvariant="normal">∠</mi><mn mathcolor="#007F00">2</mn></math></li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> صنّف المثلث أدناه تبعاً لقياسات زواياه، اختر المصطلح الأنسب.</h2>
<p><img alt="مثلث" src="https://saborah.net/app/webroot/upload/images/images/1(2329).JPG" /></p>
<ul>
<li>حاد الزوايا.</li>
<li><strong><span style="color:#27ae60;">متطابق الزوايا.</span></strong></li>
<li>منفرج الزاوية.</li>
<li>قائم الزاوية.</li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> أوجد قيمة x في متوازي الأضلاع RSTU.</h2>
<p><img alt="متوازي الأضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2330).JPG" /></p>
<ul>
<li>12</li>
<li>18</li>
<li>25</li>
<li><strong><span style="color:#27ae60;">30</span></strong></li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">4)</span></span> ما قياس كل زاوية داخلية في الخماسي المنتظم؟</h2>
<p><img alt="خماسي" src="https://saborah.net/app/webroot/upload/images/images/1(2331).JPG" /></p>
<ul>
<li>ْ96</li>
<li><span style="color:#27ae60;">ْ<strong>108</strong></span></li>
<li>ْ120</li>
<li>ْ135</li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">5)</span></span> الشكل الرباعي ABCD معين، فيه ° m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo></math>BCD = 120، أوجد m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo></math>DAC.</h2>
<p><img alt="الشكل الرباعي" src="https://saborah.net/app/webroot/upload/images/images/1(2332).JPG" /></p>
<ul>
<li>ْ30</li>
<li><span style="color:#27ae60;">ْ<strong>60</strong></span></li>
<li>ْ90</li>
<li>ْ120</li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">6)</span></span> ما قيمة x في الشكل أدناه؟</h2>
<p><img alt="تقاطع" src="https://saborah.net/app/webroot/upload/images/images/1(2333).JPG" /></p>
<ul>
<li>10</li>
<li><strong><span style="color:#27ae60;">12</span></strong></li>
<li>14</li>
<li>15</li>
</ul>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">7)</span></span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>D</mi><mi>T</mi></mrow><mo accent="false">¯</mo></mover><mo>,</mo><mover><mrow><mi>A</mi><mi>E</mi></mrow><mo accent="false">¯</mo></mover></math> قطران للمستطيل DATE يتقاطعان في S، إذا كان AE=40, ST=x+5، فما قيمة x؟</h2>
<ul>
<li>35</li>
<li>25</li>
<li><strong><span style="color:#27ae60;">15</span></strong></li>
<li>10</li>
</ul>
<h2><img alt="إجابات قصيرة" src="https://saborah.net/app/webroot/upload/images/images/1(2335).JPG" /></h2>
<h2>اكتب إجابتك في ورقة الإجابة.</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">8)</span></span> تشكّل أعمدة خيمة رؤوس سداسي منتظم، ما قياس الزاوية المتكونة عند أي من أركان الخيمة؟</h2>
<p><img alt="خسمة" src="https://saborah.net/app/webroot/upload/images/images/1(2336).JPG" /></p>
<p><span style="color:#27ae60;">G=ْ120</span></p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>6</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><msup><mn>720</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>=</mo><mfrac><mn>720</mn><mn>6</mn></mfrac><mo>=</mo><msup><mn>120</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">9)</span></span> ما إحداثيات الرأس الرابع لشبه المنحرف المتطابق الساقين LMNJ؟ بين خطوات الحل.</h2>
<p><img alt="رؤوس شبه منحرف متطابق الساقين" src="https://saborah.net/app/webroot/upload/images/images/1(2337).JPG" /></p>
<p><span style="color:#27ae60;">(-6,3)</span></p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">10)</span></span> ماذا نسمي متوازي الأضلاع إذا كان قطراه متعامدين؟ وضح إجابتك.</h2>
<p>يكون مربعاً أو معيناً.</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">11)</span></span> حدّد ما إذا كانت النتيجة صحيحة أم لا فيما يأتي اعتماداً على المعطيات، فسّر تبريرك.</h2>
<h2><span style="color:#e74c3c;">المعطيات: </span>إذا كان العدد يقبل القسمة على 9، فإنه يقبل القسمة على 3.<br />
العدد 144 يقبل القسمة على 9.</h2>
<h2><span style="color:#e74c3c;">النتيجة:</span><strong> </strong>العدد 144 يقبل القسمة على 3.</h2>
<p>النتيجة صحيحة: قانون الفصل المنطقي.</p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">12)</span></span> أوجد قيمة x في الشكل أدناه، وقرب الإجابة إلى أقرب عشر إن كان ذلك ضرورياً.</h2>
<p><img alt="شبه منحرف" src="https://saborah.net/app/webroot/upload/images/images/1(2338).JPG" /></p>
<p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mn>5</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>10</mn><mi>x</mi><mo>−</mo><mn>2</mn><mo>+</mo><mn>6</mn><mi>x</mi><mo>+</mo><mn>4</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>5</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>16</mn><mi>x</mi><mo>+</mo><mn>2</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>10</mn><mi>x</mi><mo>+</mo><mn>20</mn><mo>=</mo><mn>16</mn><mi>x</mi><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>16</mn><mi>x</mi><mo>−</mo><mn>10</mn><mi>x</mi><mo>=</mo><mn>20</mn><mo>−</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>6</mn><mi>x</mi><mo>=</mo><mn>18</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr></mtable></math></p>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">13)</span></span> ما إحداثيات مركز الدائرة التي تمر برؤوس المثلث أدناه؟</h2>
<p><img alt="التمثيل البياني" src="https://saborah.net/app/webroot/upload/images/images/1(2339).JPG" /></p>
<p>رؤوس المثلث هي (0,0)(2,0)(0,4).</p>
<p>معادلة أحد الأعمدة المنصفة هي <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">y</mi><mo mathcolor="#007F00">=</mo><mfrac mathcolor="#007F00"><mrow><mn>2</mn><mo>−</mo><mn>0</mn></mrow><mn>2</mn></mfrac><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">1</mn></math> ومعادلة عمود منصف آخر هي <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">x</mi><mo mathcolor="#007F00">=</mo><mfrac mathcolor="#007F00"><mrow><mn>4</mn><mo>−</mo><mn>0</mn></mrow><mn>2</mn></mfrac><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">2</mn></math>. ويتقاطع هذان العمودان عند النقطة (5,3) لذلك مرز الدائرة التي تمر في رؤوس المثلث يقع عند النقطة (1,2).</p>
<h2><img alt="إجابات مطولة" src="https://saborah.net/app/webroot/upload/images/images/1(2340).JPG" /></h2>
<h2>اكتب إجابتك في ورقة الإجابة مبيناً خطوات الحل.</h2>
<h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">14)</span></span> هل يمكنك إثبات أن كل شكل مما يأتي متوازي أضلاع؟ إذا لم تستطع ذلك، فاذكر المعطيات الإضافية التي ستحتاج إليها لإثبات أنه متوازي أضلاع، ووضح تبريرك.</h2>
<h2>a)</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2341).JPG" /></p>
<p>نعم، الأضلاع المتقابلة متطابقة، لذا فالشكل متوازي أضلاع.</p>
<h2>b)</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2342).JPG" /></p>
<p>لا، ضلعان متقابلان فقط متوازيان عليك أن تبين أن:</p>
<ul>
<li>الضلعان المتوازيان متطابقان أيضاً.</li>
<li>الضلعان المتقابلان الآخران متوازيان.</li>
</ul>
<h2>c)</h2>
<p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2343).JPG" /></p>
<p>نعم، الزوايا المتقابلة متطابقة لذا فالشكل متوازي أضلاع.</p>
',
'desc' => '',
'tags' => null
),
'Node' => array(
'id' => '7890',
'thumb' => null,
'parentID' => '472',
'sequence' => '0',
'has_videos' => '1'
)
)
)
$exams = array(
(int) 0 => array(
'id' => '1621',
'title' => 'اختبار الكتروني: اختبار الفصل',
'questions' => null,
'percent' => (float) NAN
)
)
$videos = array(
(int) 0 => array(
'Nodegallery' => array(
'filename' => 'i45E0Q3etrs',
'id' => '2536'
),
'Nodegallerytext' => array(
'title' => 'فيديو حل اختبار الفصل'
)
),
(int) 1 => array(
'Nodegallery' => array(
'filename' => 'msrnKmGq9mM',
'id' => '2537'
),
'Nodegallerytext' => array(
'title' => 'فيديو حل اختبار الفصل'
)
),
(int) 2 => array(
'Nodegallery' => array(
'filename' => 'pH1LGhyqYY8',
'id' => '2538'
),
'Nodegallerytext' => array(
'title' => 'فيديو حل اختبار الفصل'
)
)
)
$comments = array()
$news = array(
(int) 0 => array(
'Item' => array(
'id' => '6',
'thumb' => '1644261984.jpg'
),
'Itemtext' => array(
'name' => ' 50 الف طالب كوري يدرسون اللغة العربية في كوريا الجنوبية'
)
),
(int) 1 => array(
'Item' => array(
'id' => '8',
'thumb' => '1644262073.jpg'
),
'Itemtext' => array(
'name' => ' الشقيقان السعوديان دعاء وضياء يتصدران عباقرة العالم في الرياضيات'
)
),
(int) 2 => array(
'Item' => array(
'id' => '7',
'thumb' => '1644262036.jpg'
),
'Itemtext' => array(
'name' => ' وزير التعليم يفتتح مبنى الملحقية الثقافية في ماليزيا ويلتقي الطلبة المبتعثين'
)
)
)
$BANNERS = array(
'home-classes-up' => array(
'Zone' => array(
'adsZID' => '1',
'zoneName' => 'home-classes-up',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'home-classes-down' => array(
'Zone' => array(
'adsZID' => '2',
'zoneName' => 'home-classes-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'articles-down' => array(
'Zone' => array(
'adsZID' => '3',
'zoneName' => 'articles-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'lesson-up' => array(
'Zone' => array(
'adsZID' => '4',
'zoneName' => 'lesson-up',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'level-up' => array(
'Zone' => array(
'adsZID' => '5',
'zoneName' => 'level-up',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'lesson-down' => array(
'Zone' => array(
'adsZID' => '8',
'zoneName' => 'lesson-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array(
'Adsbanner' => array(
[maximum depth reached]
)
)
),
'level-down' => array(
'Zone' => array(
'adsZID' => '9',
'zoneName' => 'level-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'related-lessons' => array(
'Zone' => array(
'adsZID' => '10',
'zoneName' => 'related-lessons',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'article-up' => array(
'Zone' => array(
'adsZID' => '11',
'zoneName' => 'article-up',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'article-down' => array(
'Zone' => array(
'adsZID' => '12',
'zoneName' => 'article-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'question-up' => array(
'Zone' => array(
'adsZID' => '13',
'zoneName' => 'question-up',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'question-down' => array(
'Zone' => array(
'adsZID' => '14',
'zoneName' => 'question-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
),
'question-lesson-down' => array(
'Zone' => array(
'adsZID' => '15',
'zoneName' => 'question-lesson-down',
'isMultiAds' => '-1',
'zoneBreak' => null,
'isRand' => '-1'
),
'Banner' => array()
)
)
$_privilege = array()
$_menus = array()
$_nodes = array()
$_contactus = array()
$_banners = array()
$_pages = array()
$_langs = array(
(int) 0 => array(
'Lang' => array(
'id' => 'ara',
'language' => 'Arabic'
)
)
)
$request_count = (int) 998
$socical_networks = array(
(int) 0 => array(
'Confdb' => array(
'key' => 'twitter',
'value' => '#'
)
),
(int) 1 => array(
'Confdb' => array(
'key' => 'youtube',
'value' => '#'
)
),
(int) 2 => array(
'Confdb' => array(
'key' => 'linkedin',
'value' => '#'
)
)
)
$_Language = array(
'ara' => 'Arabic'
)
$Config = array(
'name_eng' => 'Saborah',
'name_ara' => 'موقع سبورة - طلاب السعودية',
'from' => 'سبورة',
'fromaddress' => 'noreply@saborah.net',
'email_monitor' => 'info@saborah.net',
'listrow' => '12',
'url' => 'https://saborah.net',
'email_formname' => 'سبورة',
'facebook' => '',
'twitter' => '#',
'youtube' => '#',
'linkedin' => '#',
'phone' => '',
'time_format' => 'H:i A',
'node_sep_slug' => '_',
'latest_update_website' => '2022-12-02 14:25:47',
'latest_login_admin' => '2022-03-16 06:26:54',
'google_secret_key' => '6LcBYhUTAAAAABPinPa4vlhvDuhne95ZnfUao0tw',
'site_key' => '6LcBYhUTAAAAAIurIcmwQzN4C2kkYLYBHyGxKWzO',
'map' => '31.99415,35.870693',
'map_center' => '31.99415,35.870693',
'keywords_ara' => 'حلول, حل, إجابات, إجابة, علوم, رياضيات, فقه, لغة, عربية, متوسط, ثانوي, الفصل, الأول, الثاني, مواد, دراسة, واجبي',
'description_ara' => 'حل الواجبات المدرسية لطلاب السعودية ف1 ف2 وجميع المواد والصفوف الدراسية من رياضيات وعلوم واجتماعيات وفقه وحاسوب',
'instagram' => '',
'admin_email' => 'mkhuder@gmail.com',
'map_zoom' => '14',
'header_code' => '<!-- Google tag (gtag.js) -->
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-216508974-1"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-216508974-1');
</script>
<!--
<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>
-->
<link rel="manifest" href="/manifest.json" > <script> const appId = "95217417-b5c7-42eb-ada0-f01acc0ba857"; const auto_register = true; //write your tags as json format //const tags = '{"key1":"value1", "key2":"value2"}'; </script> <script src="https://pushtiger.com/settings.js" ></script>',
'body_code' => '',
'website_author' => 'Sama IT Solution',
'dashboard_url' => '/admin/node/index',
'admin-panel-url' => 'backdoor',
'admin-theme-color' => '3994C7',
'email_format' => '[^@]+@[^@]+.[a-zA-Z]{2,6}',
'password_format' => '.{6,}',
'keywords_eng' => '',
'description_eng' => '',
'google-map-api-key' => 'AIzaSyBb71HgSD8EiowFnx3HRBa5pw96ChhJeMU',
'max-char-node-url' => '58',
'default-color' => '1075a9',
'api-key' => '317bbb',
'apiKey' => 'AIzaSyDQGQ05rKO5otB4_EqLW-oboBIgdDLBAUQ',
'authDomain' => 'saborah-f5614.firebaseapp.com',
'databaseURL' => 'https://saborah-f5614-default-rtdb.europe-west1.firebasedatabase.app',
'user-offline-after' => '1',
'service_account' => 'saborah-f5614-b95c91e5ec9f.json',
'thumb_width' => '400',
'min-nodes-count-view-news' => '4',
'name_default_ara' => 'سبورة',
'google-api-notification-key' => 'AAAAP5FT_i8:APA91bGmsp2e-BgVYKUO58Su2zlMp3qX6aynA4flPYpjjYEOrMD1A7zeRuC4YxVg254PcbFquFOdHKOAm5WKPyQh2wzwBVe_3HB9TSxoRokeGD21LWD4Q3wj8WShkGcEsx6iFQkqehlM',
'app-package-names' => 'net.saborah.app,net.saborah.app.fifth,net.saborah.app.sixth,net.saborah.app.seventh,net.saborah.app.eighth,net.saborah.app.ninth,net.saborah.app.thanwya,net.saborah.app.third,net.saborah.app.fourth',
'user-new-type' => '100',
'user-active-type' => '200',
'user-special-type' => '300',
'header_code_inside' => '<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>',
'google-play-app' => 'https://play.google.com/store/apps/details?id=net.saborah.app',
'header_code_inside_question' => ' <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>',
'Languages' => null
)
$headline = 'الاختبارات'
$data = array(
'id' => '1621',
'title' => 'اختبار الكتروني: اختبار الفصل',
'questions' => null,
'percent' => (float) NAN
)include - APP/View/Elements/lesson/exams.ctp, line 20 View::_evaluate() - CORE/Cake/View/View.php, line 971 View::_render() - CORE/Cake/View/View.php, line 933 View::_renderElement() - CORE/Cake/View/View.php, line 1224 View::element() - CORE/Cake/View/View.php, line 418 include - APP/View/Node/lesson.ctp, line 3 View::_evaluate() - CORE/Cake/View/View.php, line 971 View::_render() - CORE/Cake/View/View.php, line 933 View::render() - CORE/Cake/View/View.php, line 473 Controller::render() - CORE/Cake/Controller/Controller.php, line 968 NodeController::index() - APP/Controller/NodeController.php, line 263 ReflectionMethod::invokeArgs() - [internal], line ?? Controller::invokeAction() - CORE/Cake/Controller/Controller.php, line 499 Dispatcher::_invoke() - CORE/Cake/Routing/Dispatcher.php, line 193 Dispatcher::dispatch() - CORE/Cake/Routing/Dispatcher.php, line 167 [main] - APP/webroot/index.php, line 108
Notice (8): Undefined index: percent_w [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">Code Context<div class="progress" style="height: 18px;"><div class="bg-success" style="width: <?= $data['percent'] ?>%;" role="progressbar" aria-valuenow="<?= $data['percent'] ?>" aria-valuemin="0" aria-valuemax="100"></div><div class="bg-danger" style="width: <?= $data['percent_w'] ?>%;" role="progressbar" aria-valuenow="<?= $data['percent_w'] ?>" aria-valuemin="0" aria-valuemax="100"></div>$viewFile = '/home/saborah/public_html/newstyle/app/View/Elements/lesson/exams.ctp' $dataForView = array( 'GUI' => array( 'headline' => 'اختبار الفصل', 'pagetitle' => 'اختبار الفصل', 'keywords' => null, 'description' => '', 'navigation' => array( (int) 0 => array( [maximum depth reached] ), (int) 1 => array( [maximum depth reached] ), (int) 2 => array( [maximum depth reached] ), (int) 3 => array( [maximum depth reached] ), (int) 4 => array( [maximum depth reached] ) ), 'layout' => 'lesson', 'menu' => array(), 'activemenu' => '0', 'pathmenu' => array() ), 'nodes_no_icon' => array(), 'nodes_icon' => array(), 'nodes_count' => (int) 0, 'files' => array(), 'node' => array( 'Nodetext' => array( 'slug' => 'اختبار_الفصل', 'title' => 'اختبار الفصل', 'title_seo' => null, 'content' => '<h2><img alt="اختبار الفصل" src="https://saborah.net/app/webroot/upload/images/images/1(2321).JPG" /></h2> <h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> السداسي.</h2> <p>n=6</p> <p>720°=180°.(4)=180°.(6-2)=180°.(n-2)</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> ذو 16 ضلعاً.</h2> <p>n=16</p> <p>2520°=180°.(14)=180°.(16-2)=180°.(n-2)</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> <span style="color:#e74c3c;">فن:</span> تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض<br /> واعتقدت أنها ستمثل مربعاً.</h2> <h2>a) كيف يمكنها التحقق من أن الإطار مربع؟</h2> <p>إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.</p> <h2>b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.</h2> <p><img alt="مربع" src="https://saborah.net/app/webroot/upload/images/images/1(5969).JPG" /></p> <p>بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft</p> <p>وبما أن زوايا المربع الأربعة قائمة فإن y=90°</p> <h2>الشكل الرباعي ABCD شبه منحرف متطابق الساقين.</h2> <h2>4) ما الزاوية التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>C</mi></math>؟</h2> <p>حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>D</mi><mo>≅</mo><mo>∠</mo><mi>C</mi></math></p> <h2>5) ما الضلع الذي يوازي <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover></math>؟</h2> <p>حسب تعريف شبه المنحرف يكون: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover><mo>‖</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo>¯</mo></mover></math></p> <h2>6) ما القطعة المستقيمة التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover></math>؟</h2> <p>حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.</p> <p>وبالتالي فإن: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover><mo>≅</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>¯</mo></mover></math></p> <h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:</h2> <h2>7) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>1260</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p> <p>بما أن n=7 إذاً للمضلع 7 أضلاع.</p> <h2>8) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>2340</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>13</mn></mtd></mtr></mtable></math></p> <p>بما أن n=13 إذاً للمضلع 13 ضلع.</p> <h2>9) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>3240</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>18</mn></mtd></mtr></mtable></math></p> <p>بما أن n=18 إذاً للمضلع 18 ضلع.</p> <h2>10) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>5760</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>32</mn></mtd></mtr></mtable></math></p> <p>بما أن n=32 إذاً للمضلع 32 ضلع.</p> <h2>11) <span style="color:#e74c3c;">اختيار من متعدد:</span> إذا كان QRST متوازي الأضلاع، فما قيمة x؟</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6108).JPG" /></p> <ul> <li>11</li> <li>12</li> <li><span style="color:#27ae60;"><u><strong>13</strong></u></span></li> <li>14</li> </ul> <h2>إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:</h2> <h2>12) GF</h2> <p><img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1.JPG" /></p> <p>بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.</p> <p>نستعمل نظرية فيثاغورس لإيجاد GF:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mo>(</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>16</mn><mo>+</mo><mn>9</mn></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>25</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>G</mi><mi>F</mi><mo>=</mo><msqrt><mn>25</mn></msqrt><mo>=</mo><mn>5</mn><mo> </mo><mi>للطرفين</mi><mo> </mo><mi>الموجب</mi><mo> </mo><mi>التربيعي</mi><mo> </mo><mi>الجذر</mi><mo> </mo><mi>بأخذ</mi></mtd></mtr></mtable></math></p> <h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi></math></h2> <p><img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(2).JPG" /></p> <p>بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi mathvariant="normal">∠</mi><mi>G</mi></math>، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>360:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">∠</mi><mi>C</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>F</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>G</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>67</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><msup><mn>49</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi>N</mi></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>67</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>49</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>244</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2><span style="color:#e74c3c;">جبر:</span> استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6110).JPG" /></p> <h2>14) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi></math></h2> <p>بما أن قطرا المعين متعامدان فإن المثلث <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">△</mi><mi>M</mi><mi>R</mi><mi>N</mi></math> قائم وبالتالي فإن:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi><mo>=</mo><msup><mn>90</mn><mo>∘</mo></msup></math></p> <h2>15) إذا كان 12 = PR، فأوجد RN.</h2> <p>قطرا المعين ينصف كل منهما الآخر: RN=PR=12</p> <h2>16) إذا كان <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>124 = <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi></math>.</h2> <p>كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi><mo>=</mo><mfrac><mrow><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></mrow><mn>2</mn></mfrac><mo>=</mo><mfrac><msup><mn>124</mn><mo>∘</mo></msup><mn>2</mn></mfrac><mo>=</mo><msup><mn>62</mn><mo>∘</mo></msup></math></p> <h2>17) <span style="color:#e74c3c;">إنشاءات:</span> تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.</h2> <p>نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.</p> <h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>◻</mi><mi>J</mi><mi>K</mi><mi>L</mi><mi>M</mi></math> المبين جانباً لإيجاد كل مما يأتي:</h2> <p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(3).JPG" /></p> <h2>18) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi></math></h2> <p>كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>109</mn><mo>∘</mo></msup></math></p> <h2>19) JK</h2> <p>كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)</p> <p>JK=ML=6</p> <h2>20) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi></math></h2> <p>كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2><span style="color:#e74c3c;">جبر:</span> استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:</h2> <p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(4).JPG" /></p> <h2>21) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>F</mi><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn><mo>,</mo><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></math>، فاوجد EG.</h2> <p>لإيجاد EG نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mover><mrow><mi>E</mi><mi>G</mi></mrow><mo accent="false">¯</mo></mover></mtd><mtd><mo>≅</mo><mover><mrow><mi>D</mi><mi>F</mi></mrow><mo accent="false">¯</mo></mover></mtd></mtr><mtr><mtd><mi>E</mi><mi>G</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>F</mi></mtd></mtr><mtr><mtd><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></mtd><mtd><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p> <p>لحساب EG نعوض قيمة x=9:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>3</mn><mo>(</mo><mn>9</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>21</mn></math></p> <h2>22) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>,</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi><mo>=</mo><mo>(</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn><msup><mo>)</mo><mo>∘</mo></msup></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></math>.</h2> <p>نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn></mtd><mtd><mo>=</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>7</mn><mo>+</mo><mn>3</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p> <p>نعوض قيمة x=5:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><mo>(</mo><mn>5</mn><mo>(</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><msup><mn>22</mn><mo>∘</mo></msup></math></p> <h2>23) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>E</mi><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi><mo>,</mo><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></math>، فأوجد GF.</h2> <p>نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>G</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>E</mi></mtd></mtr><mtr><mtd><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>20</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr></mtable></math></p> <p>نعوض قيمة x=10:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mo>(</mo><mn>10</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>40</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>34</mn></math></p> <h2>حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.</h2> <h2>24) <img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(5).JPG" /></h2> <p>نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)</p> <h2>25) <img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 2.JPG" /></h2> <p>الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '7877', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ), 'children' => array( (int) 0 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 1 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 2 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 3 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 4 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 5 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 6 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 7 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 8 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 9 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ), (int) 10 => array( 'Nodetext' => array( [maximum depth reached] ), 'Node' => array( [maximum depth reached] ) ) ), 'exams' => array( (int) 0 => array( 'id' => '1621', 'title' => 'اختبار الكتروني: اختبار الفصل', 'questions' => null, 'percent' => (float) NAN ) ), 'videos' => array( (int) 0 => array( 'Nodegallery' => array( [maximum depth reached] ), 'Nodegallerytext' => array( [maximum depth reached] ) ), (int) 1 => array( 'Nodegallery' => array( [maximum depth reached] ), 'Nodegallerytext' => array( [maximum depth reached] ) ), (int) 2 => array( 'Nodegallery' => array( [maximum depth reached] ), 'Nodegallerytext' => array( [maximum depth reached] ) ) ), 'comments' => array(), 'news' => array( (int) 0 => array( 'Item' => array( [maximum depth reached] ), 'Itemtext' => array( [maximum depth reached] ) ), (int) 1 => array( 'Item' => array( [maximum depth reached] ), 'Itemtext' => array( [maximum depth reached] ) ), (int) 2 => array( 'Item' => array( [maximum depth reached] ), 'Itemtext' => array( [maximum depth reached] ) ) ), 'BANNERS' => array( 'home-classes-up' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'home-classes-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'articles-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'lesson-up' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'level-up' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'lesson-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array( [maximum depth reached] ) ), 'level-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'related-lessons' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'article-up' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'article-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'question-up' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'question-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ), 'question-lesson-down' => array( 'Zone' => array( [maximum depth reached] ), 'Banner' => array([maximum depth reached]) ) ), '_privilege' => array(), '_menus' => array(), '_nodes' => array(), '_contactus' => array(), '_banners' => array(), '_pages' => array(), '_langs' => array( (int) 0 => array( 'Lang' => array( [maximum depth reached] ) ) ), 'request_count' => (int) 998, 'socical_networks' => array( (int) 0 => array( 'Confdb' => array( [maximum depth reached] ) ), (int) 1 => array( 'Confdb' => array( [maximum depth reached] ) ), (int) 2 => array( 'Confdb' => array( [maximum depth reached] ) ) ), '_Language' => array( 'ara' => 'Arabic' ), 'Config' => array( 'name_eng' => 'Saborah', 'name_ara' => 'موقع سبورة - طلاب السعودية', 'from' => 'سبورة', 'fromaddress' => 'noreply@saborah.net', 'email_monitor' => 'info@saborah.net', 'listrow' => '12', 'url' => 'https://saborah.net', 'email_formname' => 'سبورة', 'facebook' => '', 'twitter' => '#', 'youtube' => '#', 'linkedin' => '#', 'phone' => '', 'time_format' => 'H:i A', 'node_sep_slug' => '_', 'latest_update_website' => '2022-12-02 14:25:47', 'latest_login_admin' => '2022-03-16 06:26:54', 'google_secret_key' => '6LcBYhUTAAAAABPinPa4vlhvDuhne95ZnfUao0tw', 'site_key' => '6LcBYhUTAAAAAIurIcmwQzN4C2kkYLYBHyGxKWzO', 'map' => '31.99415,35.870693', 'map_center' => '31.99415,35.870693', 'keywords_ara' => 'حلول, حل, إجابات, إجابة, علوم, رياضيات, فقه, لغة, عربية, متوسط, ثانوي, الفصل, الأول, الثاني, مواد, دراسة, واجبي', 'description_ara' => 'حل الواجبات المدرسية لطلاب السعودية ف1 ف2 وجميع المواد والصفوف الدراسية من رياضيات وعلوم واجتماعيات وفقه وحاسوب', 'instagram' => '', 'admin_email' => 'mkhuder@gmail.com', 'map_zoom' => '14', 'header_code' => '<!-- Google tag (gtag.js) --> <script async src="https://www.googletagmanager.com/gtag/js?id=UA-216508974-1"></script> <script> window.dataLayer = window.dataLayer || []; function gtag(){dataLayer.push(arguments);} gtag('js', new Date()); gtag('config', 'UA-216508974-1'); </script> <!-- <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script> --> <link rel="manifest" href="/manifest.json" > <script> const appId = "95217417-b5c7-42eb-ada0-f01acc0ba857"; const auto_register = true; //write your tags as json format //const tags = '{"key1":"value1", "key2":"value2"}'; </script> <script src="https://pushtiger.com/settings.js" ></script>', 'body_code' => '', 'website_author' => 'Sama IT Solution', 'dashboard_url' => '/admin/node/index', 'admin-panel-url' => 'backdoor', 'admin-theme-color' => '3994C7', 'email_format' => '[^@]+@[^@]+.[a-zA-Z]{2,6}', 'password_format' => '.{6,}', 'keywords_eng' => '', 'description_eng' => '', 'google-map-api-key' => 'AIzaSyBb71HgSD8EiowFnx3HRBa5pw96ChhJeMU', 'max-char-node-url' => '58', 'default-color' => '1075a9', 'api-key' => '317bbb', 'apiKey' => 'AIzaSyDQGQ05rKO5otB4_EqLW-oboBIgdDLBAUQ', 'authDomain' => 'saborah-f5614.firebaseapp.com', 'databaseURL' => 'https://saborah-f5614-default-rtdb.europe-west1.firebasedatabase.app', 'user-offline-after' => '1', 'service_account' => 'saborah-f5614-b95c91e5ec9f.json', 'thumb_width' => '400', 'min-nodes-count-view-news' => '4', 'name_default_ara' => 'سبورة', 'google-api-notification-key' => 'AAAAP5FT_i8:APA91bGmsp2e-BgVYKUO58Su2zlMp3qX6aynA4flPYpjjYEOrMD1A7zeRuC4YxVg254PcbFquFOdHKOAm5WKPyQh2wzwBVe_3HB9TSxoRokeGD21LWD4Q3wj8WShkGcEsx6iFQkqehlM', 'app-package-names' => 'net.saborah.app,net.saborah.app.fifth,net.saborah.app.sixth,net.saborah.app.seventh,net.saborah.app.eighth,net.saborah.app.ninth,net.saborah.app.thanwya,net.saborah.app.third,net.saborah.app.fourth', 'user-new-type' => '100', 'user-active-type' => '200', 'user-special-type' => '300', 'header_code_inside' => '<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>', 'google-play-app' => 'https://play.google.com/store/apps/details?id=net.saborah.app', 'header_code_inside_question' => ' <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>', 'Languages' => null ), 'headline' => 'الاختبارات' ) $GUI = array( 'headline' => 'اختبار الفصل', 'pagetitle' => 'اختبار الفصل', 'keywords' => null, 'description' => '', 'navigation' => array( (int) 0 => array( 'name' => 'الثانوية مقررات', 'url' => '/lesson/39/الثانوية_مقررات' ), (int) 1 => array( 'name' => 'المسار المشترك', 'url' => '/lesson/470/المسار_المشترك' ), (int) 2 => array( 'name' => 'الرياضيات 2', 'url' => '/lesson/471/الرياضيات_2' ), (int) 3 => array( 'name' => 'الفصل الأول: الأشكال الرباعية', 'url' => '/lesson/472/الفصل_الأول_الأشكال_الرباعية' ), (int) 4 => array( 'name' => 'اختبار الفصل', 'url' => '/lesson/7877/اختبار_الفصل' ) ), 'layout' => 'lesson', 'menu' => array(), 'activemenu' => '0', 'pathmenu' => array() ) $nodes_no_icon = array() $nodes_icon = array() $nodes_count = (int) 0 $files = array() $node = array( 'Nodetext' => array( 'slug' => 'اختبار_الفصل', 'title' => 'اختبار الفصل', 'title_seo' => null, 'content' => '<h2><img alt="اختبار الفصل" src="https://saborah.net/app/webroot/upload/images/images/1(2321).JPG" /></h2> <h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> السداسي.</h2> <p>n=6</p> <p>720°=180°.(4)=180°.(6-2)=180°.(n-2)</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> ذو 16 ضلعاً.</h2> <p>n=16</p> <p>2520°=180°.(14)=180°.(16-2)=180°.(n-2)</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> <span style="color:#e74c3c;">فن:</span> تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض<br /> واعتقدت أنها ستمثل مربعاً.</h2> <h2>a) كيف يمكنها التحقق من أن الإطار مربع؟</h2> <p>إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.</p> <h2>b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.</h2> <p><img alt="مربع" src="https://saborah.net/app/webroot/upload/images/images/1(5969).JPG" /></p> <p>بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft</p> <p>وبما أن زوايا المربع الأربعة قائمة فإن y=90°</p> <h2>الشكل الرباعي ABCD شبه منحرف متطابق الساقين.</h2> <h2>4) ما الزاوية التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>C</mi></math>؟</h2> <p>حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>D</mi><mo>≅</mo><mo>∠</mo><mi>C</mi></math></p> <h2>5) ما الضلع الذي يوازي <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover></math>؟</h2> <p>حسب تعريف شبه المنحرف يكون: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>¯</mo></mover><mo>‖</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo>¯</mo></mover></math></p> <h2>6) ما القطعة المستقيمة التي تطابق <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover></math>؟</h2> <p>حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.</p> <p>وبالتالي فإن: <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>¯</mo></mover><mo>≅</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>¯</mo></mover></math></p> <h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:</h2> <h2>7) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>900 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>1260</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p> <p>بما أن n=7 إذاً للمضلع 7 أضلاع.</p> <h2>8) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>1890 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>1980</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>2340</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>13</mn></mtd></mtr></mtable></math></p> <p>بما أن n=13 إذاً للمضلع 13 ضلع.</p> <h2>9) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>2880 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>3240</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>18</mn></mtd></mtr></mtable></math></p> <p>بما أن n=18 إذاً للمضلع 18 ضلع.</p> <h2>10) <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400</h2> <p>عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>5400 هو حل المعادلة:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>−</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>180</mn><mo>∘</mo></msup><mi>n</mi><mo>=</mo><msup><mn>5400</mn><mo>∘</mo></msup><mo>+</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mfrac><msup><mn>5760</mn><mo>∘</mo></msup><msup><mn>180</mn><mo>∘</mo></msup></mfrac><mo>=</mo><mn>32</mn></mtd></mtr></mtable></math></p> <p>بما أن n=32 إذاً للمضلع 32 ضلع.</p> <h2>11) <span style="color:#e74c3c;">اختيار من متعدد:</span> إذا كان QRST متوازي الأضلاع، فما قيمة x؟</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6108).JPG" /></p> <ul> <li>11</li> <li>12</li> <li><span style="color:#27ae60;"><u><strong>13</strong></u></span></li> <li>14</li> </ul> <h2>إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:</h2> <h2>12) GF</h2> <p><img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1.JPG" /></p> <p>بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.</p> <p>نستعمل نظرية فيثاغورس لإيجاد GF:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mo>(</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>16</mn><mo>+</mo><mn>9</mn></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mi>G</mi><mi>F</mi><msup><mo>)</mo><mn>2</mn></msup><mo>=</mo><mn>25</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>G</mi><mi>F</mi><mo>=</mo><msqrt><mn>25</mn></msqrt><mo>=</mo><mn>5</mn><mo> </mo><mi>للطرفين</mi><mo> </mo><mi>الموجب</mi><mo> </mo><mi>التربيعي</mi><mo> </mo><mi>الجذر</mi><mo> </mo><mi>بأخذ</mi></mtd></mtr></mtable></math></p> <h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi></math></h2> <p><img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(2).JPG" /></p> <p>بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi mathvariant="normal">∠</mi><mi>G</mi></math>، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>360:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">∠</mi><mi>C</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>F</mi><mo>+</mo><mi mathvariant="normal">∠</mi><mi>G</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><msup><mn>67</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>+</mo><msup><mn>49</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><mi>N</mi></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>67</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>49</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>244</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2><span style="color:#e74c3c;">جبر:</span> استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(6110).JPG" /></p> <h2>14) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi></math></h2> <p>بما أن قطرا المعين متعامدان فإن المثلث <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">△</mi><mi>M</mi><mi>R</mi><mi>N</mi></math> قائم وبالتالي فإن:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>M</mi><mi>R</mi><mi>N</mi><mo>=</mo><msup><mn>90</mn><mo>∘</mo></msup></math></p> <h2>15) إذا كان 12 = PR، فأوجد RN.</h2> <p>قطرا المعين ينصف كل منهما الآخر: RN=PR=12</p> <h2>16) إذا كان <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mo>°</mo></math>124 = <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi></math>.</h2> <p>كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>M</mi><mo>=</mo><mfrac><mrow><mi mathvariant="normal">∠</mi><mi>P</mi><mi>O</mi><mi>N</mi></mrow><mn>2</mn></mfrac><mo>=</mo><mfrac><msup><mn>124</mn><mo>∘</mo></msup><mn>2</mn></mfrac><mo>=</mo><msup><mn>62</mn><mo>∘</mo></msup></math></p> <h2>17) <span style="color:#e74c3c;">إنشاءات:</span> تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.</h2> <p>نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.</p> <h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>◻</mi><mi>J</mi><mi>K</mi><mi>L</mi><mi>M</mi></math> المبين جانباً لإيجاد كل مما يأتي:</h2> <p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(3).JPG" /></p> <h2>18) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi></math></h2> <p>كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>M</mi><mi>L</mi><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>109</mn><mo>∘</mo></msup></math></p> <h2>19) JK</h2> <p>كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)</p> <p>JK=ML=6</p> <h2>20) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi></math></h2> <p>كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>J</mi><mi>K</mi><mi>L</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>+</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>K</mi><mi>L</mi><mi>M</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>109</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2><span style="color:#e74c3c;">جبر:</span> استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:</h2> <p><img alt="الشكل" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(4).JPG" /></p> <h2>21) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>F</mi><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn><mo>,</mo><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></math>، فاوجد EG.</h2> <p>لإيجاد EG نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mover><mrow><mi>E</mi><mi>G</mi></mrow><mo accent="false">¯</mo></mover></mtd><mtd><mo>≅</mo><mover><mrow><mi>D</mi><mi>F</mi></mrow><mo accent="false">¯</mo></mover></mtd></mtr><mtr><mtd><mi>E</mi><mi>G</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>F</mi></mtd></mtr><mtr><mtd><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo></mtd><mtd><mo>=</mo><mn>2</mn><mo>(</mo><mi>x</mi><mo>+</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>−</mo><mn>7</mn></mtd></mtr><mtr><mtd><mi>x</mi><mo>−</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p> <p>لحساب EG نعوض قيمة x=9:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>G</mi><mo>=</mo><mn>3</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>3</mn><mi>x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>3</mn><mo>(</mo><mn>9</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>21</mn></math></p> <h2>22) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>,</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi><mo>=</mo><mo>(</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn><msup><mo>)</mo><mo>∘</mo></msup></math>، فأوجد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></math>.</h2> <p>نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mi>F</mi><mi>G</mi></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn></mtd><mtd><mo>=</mo><mn>3</mn><mi>x</mi><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>7</mn><mo>+</mo><mn>3</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p> <p>نعوض قيمة x=5:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mi mathvariant="normal">∠</mi><mi>E</mi><mi>D</mi><mi>F</mi><mo>=</mo><mo>(</mo><mn>5</mn><mi>x</mi><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><mo>(</mo><mn>5</mn><mo>(</mo><mn>5</mn><mo>)</mo><mo>−</mo><mn>3</mn><msup><mo>)</mo><mo>∘</mo></msup><mo>=</mo><msup><mn>22</mn><mo>∘</mo></msup></math></p> <h2>23) إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>E</mi><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi><mo>,</mo><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></math>، فأوجد GF.</h2> <p>نوجد قيمة x:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>G</mi><mi>F</mi></mtd><mtd><mo>=</mo><mi>D</mi><mi>E</mi></mtd></mtr><mtr><mtd><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>2</mn><mi>x</mi></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>14</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi></mtd><mtd><mo>=</mo><mn>20</mn></mtd></mtr><mtr><mtd><mi>x</mi></mtd><mtd><mo>=</mo><mn>10</mn></mtd></mtr></mtable></math></p> <p>نعوض قيمة x=10:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>G</mi><mi>F</mi><mo>=</mo><mn>4</mn><mo>(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo>)</mo><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>12</mn><mo>+</mo><mn>6</mn><mo>=</mo><mn>4</mn><mo>(</mo><mn>10</mn><mo>)</mo><mo>−</mo><mn>6</mn><mo>=</mo><mn>40</mn><mo>−</mo><mn>6</mn><mo>=</mo><mn>34</mn></math></p> <h2>حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.</h2> <h2>24) <img alt="الشكل 1" src="https://saborah.net/app/webroot/upload/images/images/الشكل 1(5).JPG" /></h2> <p>نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)</p> <h2>25) <img alt="الشكل 2" src="https://saborah.net/app/webroot/upload/images/images/الشكل 2.JPG" /></h2> <p>الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '7877', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ) $children = array( (int) 0 => array( 'Nodetext' => array( 'slug' => 'التهيئة_للفصل_الأول', 'title' => 'التهيئة للفصل الأول', 'title_seo' => null, 'content' => '<p><img alt="التهيئة للفصل الاول" src="https://saborah.net/app/webroot/upload/images/images/التهيئة للفصل الأول.JPG" /></p> <h2>أجب عن الاختبار الآتي انظر المراجعة السريعة قبل الإجابة عن الاختبار.</h2> <h2><img alt="اختبار سريع" src="https://saborah.net/app/webroot/upload/images/images/Capture(1).JPG" /><br /> أوجد قيم x,y في كل مما يأتي مقرباً إلى أقرب عشر:</h2> <h2>1)</h2> <p><img alt="مثلث 1" src="https://saborah.net/app/webroot/upload/images/images/مثلث 1.JPG" /></p> <p><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></p> <p>الزاوية الخارجية عن المثلث = مجموع الزاويتين الداخليتين البعيدتين.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>4</mn><mi>x</mi><mo>=</mo><mn>83</mn><mo>+</mo><mi>x</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>−</mo><mi>x</mi><mo>=</mo><mn>83</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>=</mo><mn>83</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>27.7</mn></mtd></mtr></mtable></math></p> <h2>2)</h2> <p><img alt="مثلث 2" src="https://saborah.net/app/webroot/upload/images/images/مثلث 2.JPG" /></p> <p><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></p> <p>بما أن المثلث جميع أضلاعه متطابقة إذاً:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="0em"><mtr><mtd><mn>9</mn><mi>x</mi><mo>=</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>4</mn><mi>x</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>5</mn><mi>x</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>1</mn></mtd></mtr></mtable></math></p> <p>بما أن المثلث جميع أضلاعه متطابقة إذاً: جميع زواياه متطابقة و = <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>60</mn><mo>°</mo></math>.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo> </mo><mo>=</mo><mo> </mo><mn>180</mn><mo> </mo><mo>-</mo><mn>60</mn><mspace linebreak="newline"></mspace><mi>y</mi><mo> </mo><mo>=</mo><mo> </mo><mn>120</mn><mo>°</mo></math></p> <h2>3) <span style="color:#e74c3c;">مدن:</span> تمثل مواقع كل من الرياض وجدة وأبها رؤوس مثلث كما في الشكل أدناه إذا كان محيط هذا المثلث 2198km فأوجد المسافة الجوية بين كل من المدن الثلاث.</h2> <h2><img alt="مثلث 3" src="https://saborah.net/app/webroot/upload/images/images/مثلث 3.JPG" /></h2> <h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2> <p>محيط المثلث = مجموع أطوال أضلاعه.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>=</mo><mo> </mo><mfenced><mrow><mn>53</mn><mo>.</mo><mn>4</mn><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>80</mn><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>90</mn><mo> </mo><mo>+</mo><mo> </mo><mn>88</mn><mo>.</mo><mn>5</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>2198</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mfenced><mrow><mn>221</mn><mo>.</mo><mn>9</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>90</mn><mo> </mo><mo>-</mo><mo> </mo><mn>2198</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mfenced><mrow><mn>221</mn><mo>.</mo><mn>9</mn><mo> </mo><mi>x</mi></mrow></mfenced><mo> </mo><mo>=</mo><mo> </mo><mn>2108</mn><mspace linebreak="newline"></mspace><mspace linebreak="newline"></mspace><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mi>x</mi><mo> </mo><mo>=</mo><mo> </mo><mn>9</mn><mo>.</mo><mn>5</mn></math></p> <ul> <li>المسافة بين الرياض وجدة = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mn>90</mn><mo> </mo><mo>+</mo><mo> </mo><mi mathvariant="normal">x</mi><mn>80</mn><mo> </mo><mo>=</mo><mo> </mo><mn>90</mn><mo> </mo><mo>+</mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>80</mn><mo> </mo><mo>=</mo><mn>850</mn></math>.</li> <li>المسافة بين الرياض وأبها = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mn>5</mn><mo>.</mo><mn>88</mn><mo> </mo><mo>=</mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>5</mn><mo>.</mo><mn>88</mn><mo> </mo><mo>=</mo><mo> </mo><mn>8</mn><mo>.</mo><mn>840</mn></math>.</li> <li>المسافة بين جدة وأبها = <math dir="rtl" xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mn>4</mn><mo>.</mo><mn>53</mn><mo> </mo><mo>=</mo><mo> </mo><mn>5</mn><mo>.</mo><mn>9</mn><mo> </mo><mo>×</mo><mn>4</mn><mo>.</mo><mn>53</mn><mo> </mo><mo>=</mo><mo> </mo><mn>3</mn><mo>.</mo><mn>507</mn></math>.</li> </ul> <h2>حدد ما إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> متوازيين أو متعامدين أو غير ذلك في كل مما يأتي:</h2> <h2 style="direction: ltr; text-align: right;">.A(3,3),B(8,2),C(6, -1),D(1,0) (4</h2> <h2 style="direction: ltr; text-align: right;"><span style="color:#c0392b;">:الحل</span></h2> <h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>−</mo><mn>3</mn></mrow><mrow><mn>8</mn><mo>−</mo><mn>3</mn></mrow></mfrac><mo> </mo><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>AB</mi><mo> </mo></mrow><mo>→</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>1</mn><mrow><mo>−</mo><mn>5</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>0</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>1</mn><mo>−</mo><mn>6</mn></mrow></mfrac><mo> </mo><mo>:</mo><mover accent="true"><mrow><mo> </mo><mi>CD</mi></mrow><mo>↔</mo></mover><mtext> ميل  </mtext></mtd></mtr></mtable></math></h2> <p style="direction: ltr; text-align: right;">.بما أن ميل كل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> متساويين إذاً فهما متوازيين</p> <h2 style="direction: ltr; text-align: right;">.A(4,2),B(1,-3),C(-3,5),D(2,2) (5</h2> <h2 style="direction: ltr; text-align: right;"><font color="#c0392b"><span style="font-size: 16px;"><b>:الحل</b></span></font></h2> <h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>5</mn><mn>3</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn></mrow><mrow><mo>−</mo><mn>3</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>2</mn></mrow><mrow><mn>1</mn><mo>−</mo><mn>4</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>AB</mi><mo> </mo></mrow><mo>↔</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>3</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>−</mo><mn>5</mn></mrow><mrow><mn>2</mn><mo>−</mo><mo>(</mo><mo>−</mo><mn>3</mn><mo>)</mo></mrow></mfrac><mo> </mo><mo>:</mo><mo> </mo><mover accent="true"><mrow><mi>CD</mi><mo> </mo></mrow><mo>↔</mo></mover><mi>ميل</mi><mo> </mo></mtd></mtr></mtable></math></h2> <p style="direction: ltr; text-align: right;">.بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> حاصل ضربهم = -1 إذاً فهما متعامدان</p> <h2 style="direction: ltr; text-align: right;">.A(-8,-7),B(4,-4),C(-2,-5),D(1,7) (6</h2> <h2 style="direction: ltr; text-align: right;"><span style="color:#c0392b;">:الحل</span></h2> <h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnspacing="1em"><mtr><mtd><mi>m</mi><mo>=</mo><mfrac><mrow><msub><mi>y</mi><mn>2</mn></msub><mo>−</mo><msub><mi>y</mi><mn>1</mn></msub></mrow><mrow><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>1</mn><mn>4</mn></mfrac><mo>=</mo><mfrac><mn>3</mn><mn>12</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>4</mn><mo>+</mo><mn>7</mn></mrow><mrow><mn>4</mn><mo>+</mo><mn>8</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mrow><mi>A</mi><mi>B</mi><mo> </mo></mrow><mo>↔</mo></mover><mtext> ميل  </mtext></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mo>=</mo><mfrac><mn>12</mn><mn>3</mn></mfrac><mo>=</mo><mfrac><mrow><mn>7</mn><mo>+</mo><mn>5</mn></mrow><mrow><mn>1</mn><mo>+</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mrow><mi>C</mi><mi>D</mi><mo> </mo></mrow><mo>↔</mo></mover><mtext>ميل</mtext></mtd></mtr></mtable></math></h2> <p style="direction: ltr; text-align: right;">.بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>C</mi><mi>D</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo>↔</mo></mover></math> غير متساويين فهما غير متوازيين وليس حاصل ضربهم =-1 إذا فهمت غير ذلك</p> <h2>7) <span style="color:#e74c3c;">حدائق:</span> صمم مهندس رسماً لحديقة رباعية الشكل إحداثيات رؤوسها: A(-2,1),B(3,-3),C(5,7),D(-3 ,4) إذا رسم ممرين يقطعانها <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>↔</mo></mover></math>, فهل الممران متعامدان؟ فسر اجابتك.</h2> <h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2> <h2><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mi mathvariant="normal">m</mi><mo>=</mo><mfrac><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfrac></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>7</mn></mrow><mn>6</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>4</mn></mrow><mrow><mn>3</mn><mo>+</mo><mn>3</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mi>BD</mi><mo>↔</mo></mover><mo> </mo><mi>ميل</mi><mo> </mo></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>6</mn><mn>7</mn></mfrac><mo>=</mo><mfrac><mrow><mn>7</mn><mo>−</mo><mn>1</mn></mrow><mrow><mn>5</mn><mo>+</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mo> </mo><mover accent="true"><mi>AC</mi><mo>↔</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr></mtable></math></h2> <p>بما أن ميل كل من <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>C</mi><mi>ِ</mi><mi>ِ</mi></mrow><mo>↔</mo></mover><mo> </mo><mo>,</mo><mover><mrow><mi>B</mi><mi>D</mi></mrow><mo>↔</mo></mover></math> حاصل ضربهم = -1 إذاً فهما متعامدان.</p> <h2>أوجد المسافة بين كل نقطتين ثم أوجد احداثيات نقطة منتصف القطعة الواصلة بينهما في كل مما يأتي:</h2> <h2 style="direction: ltr; text-align: right;">.J(-6,2),K(-1,3) (8</h2> <h2 style="direction: ltr; text-align: right;"><strong><span style="color:#c0392b;"><span style="font-size:16px;">:الحل</span></span></strong></h2> <h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>JK</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>3</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>26</mn></msqrt></mtd></mtr></mtable></math></h2> <h2 style="direction: ltr; text-align: right;">.R(2,5),S(8,4) (9</h2> <h2 style="direction: ltr; text-align: right;"><strong><span style="color:#c0392b;"><span style="font-size:16px;">:الحل</span></span></strong></h2> <h2 style="direction: ltr; text-align: right;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">8</mn><mo>−</mo><mn mathvariant="bold">2</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">4</mn><mo>−</mo><mn mathvariant="bold">5</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">RS</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">6</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn mathvariant="bold">1</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>37</mn></msqrt></mtd></mtr></mtable></math></h2> <h2>10) <span style="color:#e74c3c;">مسافات:</span> وقف شخص على النقطة (20,80)T من مستوى احداثي ورغب في الانتقال الى كل من (60,20)U و(85,110)V فما أقصر مسافة يمكن أن يقطعها الشخص؟ فسر اجابتك.</h2> <h2><strong><span style="color:#c0392b;"><span style="font-size:16px;">الحل:</span></span></strong></h2> <h2><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">20</mn><mo>−</mo><mn mathvariant="bold">80</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">60</mn><mo>−</mo><mn mathvariant="bold">20</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TU</mi><mo>=</mo><msqrt><mo>(</mo><mo>−</mo><mn mathvariant="bold">60</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">40</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><mn>20</mn><msqrt><mn>13</mn></msqrt><mo>=</mo><mn>72.11</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="bold">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="bold">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">110</mn><mo>−</mo><mn mathvariant="bold">80</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">85</mn><mo>−</mo><mn mathvariant="bold">20</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="bold">TV</mi><mo>=</mo><msqrt><mo>(</mo><mn mathvariant="bold">30</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn mathvariant="bold">65</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><mn mathvariant="bold">5</mn><msqrt><mn mathvariant="bold">205</mn></msqrt><mo>=</mo><mn>71.6</mn></mtd></mtr></mtable></math></h2> <p>أقصر مسافة يقطعها الشخص هي من النقطة T إلى U >.</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '490', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ), (int) 1 => array( 'Nodetext' => array( 'slug' => 'الدرس_الأول_زوايا_المضلع', 'title' => 'الدرس الأول: زوايا المضلع', 'title_seo' => 'حل درس زوايا المضلع - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '526', 'thumb' => null, 'parentID' => '472', 'sequence' => '1', 'has_videos' => '1' ) ), (int) 2 => array( 'Nodetext' => array( 'slug' => 'الدرس_الثاني_متوازي_الأضلاع', 'title' => 'الدرس الثاني: متوازي الأضلاع', 'title_seo' => 'حل درس متوازي الأضلاع - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '617', 'thumb' => null, 'parentID' => '472', 'sequence' => '2', 'has_videos' => '1' ) ), (int) 3 => array( 'Nodetext' => array( 'slug' => 'الدرس_الثالث_تمييز_متوازي_الأضلاع', 'title' => 'الدرس الثالث: تمييز متوازي الأضلاع', 'title_seo' => 'حل درس تمييز متوازي الأضلاع - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '679', 'thumb' => null, 'parentID' => '472', 'sequence' => '3', 'has_videos' => '1' ) ), (int) 4 => array( 'Nodetext' => array( 'slug' => 'اختبار_منتصف_الفصل', 'title' => 'اختبار منتصف الفصل', 'title_seo' => null, 'content' => '<p><img alt="حل اخبار منصف" src="https://saborah.net/app/webroot/upload/images/images/عناون اختبار.JPG" /></p> <h2>أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعات المحدبة الآتية: (الدرس 1-1).</h2> <h2>1) الخماسي:</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>5</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>5</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>540</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>2) السباعي:</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>7</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>7</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>900</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>3) ذو 18 ضلعاً:</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>18</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>18</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>2880</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>4) ذو 23 ضلعاً:</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">n</mi><mo>=</mo><mn>23</mn></mtd></mtr><mtr><mtd><mo>(</mo><mi mathvariant="normal">n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>23</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>=</mo><msup><mn>3780</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>أوجد قياسات جميع الزوايا في كل من المضلعين الآتيين: (الدرس 1-1).</h2> <h2>5)</h2> <p><img alt="شكل 5" src="https://saborah.net/app/webroot/upload/images/images/5(11).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mn>4</mn><mi>x</mi><mo>−</mo><mn>26</mn><mo>+</mo><mi>x</mi><mo>+</mo><mi>x</mi><mo>+</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>18</mn><mo>)</mo><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>8</mn><mi>x</mi><mo>−</mo><mn>8</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>46</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>A</mi><mo>=</mo><mn>4</mn><mo>×</mo><mn>46</mn><mo>−</mo><mn>26</mn><mo>=</mo><msup><mn>158</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>C</mi><mo>=</mo><mn>2</mn><mo>×</mo><mn>46</mn><mo>+</mo><mn>18</mn><mo>=</mo><msup><mn>110</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>B</mi><mo>=</mo><msup><mn>46</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>m</mi><mi mathvariant="normal">∠</mi><mi>D</mi><mo>=</mo><msup><mn>46</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>6)</h2> <p><img alt="شكل 6" src="https://saborah.net/app/webroot/upload/images/images/6(9).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>16</mn><mo>+</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>+</mo><mi mathvariant="normal">x</mi><mo>+</mo><mi mathvariant="normal">x</mi><mo>+</mo><mn>10</mn><mo>)</mo><mo>=</mo><msup><mn>360</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>6</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">x</mi><mo>=</mo><mn>61</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">Q</mi><mo>=</mo><mn>2</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>16</mn><mo>=</mo><mn>2</mn><mo>×</mo><mn>61</mn><mo>−</mo><mn>16</mn><mo>=</mo><msup><mn>106</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">R</mi><mo>=</mo><mn>2</mn><mo>×</mo><mn>61</mn><mo>=</mo><msup><mn>122</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">P</mi><mo>=</mo><msup><mn>61</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">m</mi><mi mathvariant="normal">∠</mi><mi mathvariant="normal">S</mi><mo>=</mo><mi mathvariant="normal">x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mn>61</mn><mo>+</mo><mn>10</mn><mo>=</mo><msup><mn>71</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه الداخلية في كل مما يأتي:</h2> <h2>7) 720º</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>720</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>720</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>720</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>6</mn></mtd></mtr></mtable></math></p> <h2>8) 1260º</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>1260</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1260</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1260</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>9</mn></mtd></mtr></mtable></math></p> <h2>9) 1800º</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>1800</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1800</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>1800</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>12</mn></mtd></mtr></mtable></math></p> <h2>10) 4500º</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>4500</mn><mo>=</mo><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4500</mn><mo>=</mo><mn>180</mn><mi>n</mi><mo>−</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4500</mn><mo>+</mo><mn>360</mn><mo>=</mo><mn>180</mn><mi>n</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>n</mi><mo>=</mo><mn>27</mn></mtd></mtr></mtable></math></p> <h2>أوجد قيمة x في كل من الشكلين الآتيين:</h2> <h2>11)</h2> <p><img alt="شكل 11" src="https://saborah.net/app/webroot/upload/images/images/11(9).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mi>x</mi><mo>+</mo><mn>15</mn><mo>)</mo><mo>+</mo><mn>106</mn><mo>+</mo><mo>(</mo><mi>x</mi><mo>−</mo><mn>10</mn><mo>)</mo><mo>+</mo><mo>(</mo><mn>2</mn><mi>x</mi><mo>−</mo><mn>35</mn><mo>)</mo><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>+</mo><mn>76</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>71</mn></mtd></mtr></mtable></math></p> <h2>12)</h2> <p><img alt="شكل 12" src="https://saborah.net/app/webroot/upload/images/images/12(9).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mo>(</mo><mi>x</mi><mo>+</mo><mn>4</mn><mo>)</mo><mo>+</mo><mn>56</mn><mo>+</mo><mo>(</mo><mi>x</mi><mo>+</mo><mn>10</mn><mo>)</mo><mo>+</mo><mo>(</mo><mi>x</mi><mo>−</mo><mn>6</mn><mo>)</mo><mo>+</mo><mi>x</mi><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>x</mi><mo>+</mo><mn>64</mn><mo>=</mo><mn>360</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>74</mn></mtd></mtr></mtable></math></p> <h2>استعمل <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>W</mi><mi>X</mi><mi>Y</mi><mi>Z</mi></math> لإيجاد كل مما يأتي:</h2> <h2><img alt="شكل 13" src="https://saborah.net/app/webroot/upload/images/images/13(7).JPG" /></h2> <h2>13) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>W</mi><mi>Z</mi><mi>Y</mi></math></h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><msup><mn>105</mn><mo>∘</mo></msup><mo>+</mo><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>180</mn><mo>∘</mo></msup><mo>−</mo><msup><mn>105</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">∠</mi><mi>W</mi><mi>Z</mi><mi>Y</mi><mo>=</mo><msup><mn>75</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2>14) WZ</h2> <p>الحل:</p> <p>WZ = XY =24</p> <h2>15) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>X</mi><mi>Y</mi><mi>Z</mi></math></h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>X</mi><mi>Y</mi><mi>Z</mi><mo> </mo><mo>=</mo><mo> </mo><mo>∠</mo><mi>Z</mi><mi>W</mi><mi>X</mi><mo> </mo><mo>=</mo><mo> </mo><mn>105</mn><mo>°</mo></math></p> <h2>16) <span style="color:#e74c3c;">إنارة:</span> استعمل مقبض الانارة العلوي الذي يشكل متوازي أضلاع في إيجاد <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>m</mi><mo>∠</mo><mi>p</mi></math> في <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>P</mi><mi>Q</mi><mi>R</mi><mi>S</mi></math>.</h2> <p><img alt="شكل 16" src="https://saborah.net/app/webroot/upload/images/images/16(4).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>S</mi><mo> </mo><mi>و</mi><mo> </mo><mo>∠</mo><mi>P</mi></math> زاويتان متكاملتان.</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>P</mi><mo> </mo><mo>=</mo><mo> </mo><mn>180</mn><mo> </mo><mo>-</mo><mn>64</mn><mo> </mo><mo>=</mo><mn>116</mn><mo>°</mo></math></p> <h2><span style="color:#e74c3c;">جبر:</span> أوجد قيم المتغيرات في كل من متوازيي الأضلاع الآتيين: (الدرس 2-1).</h2> <h2>17)</h2> <p><img alt="شكل 17" src="https://saborah.net/app/webroot/upload/images/images/17(3).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi mathvariant="normal">s</mi><mo>−</mo><mn>7</mn><mo>=</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">s</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>7</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">s</mi><mo>=</mo><mn>13</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">t</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi mathvariant="normal">t</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi mathvariant="normal">t</mi><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p> <h2>18)</h2> <p><img alt="شكل 18" src="https://saborah.net/app/webroot/upload/images/images/18(3).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>3</mn><mi>f</mi><mo>−</mo><mn>6</mn><mo>=</mo><mn>2</mn><mi>f</mi><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>f</mi><mo>−</mo><mn>2</mn><mi>f</mi><mo>=</mo><mn>8</mn><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>f</mi><mo>=</mo><mn>14</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>56</mn><mo>+</mo><mo>(</mo><mn>3</mn><mi>d</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>=</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>54</mn><mo>+</mo><mn>3</mn><mi>d</mi><mo>=</mo><mn>180</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>d</mi><mo>=</mo><mn>180</mn><mo>−</mo><mn>54</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>d</mi><mo>=</mo><mn>126</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>d</mi><mo>=</mo><mn>42</mn></mtd></mtr></mtable></math></p> <h2>19)<span style="color:#e74c3c;"> برهان: </span>اكتب برهاناً ذا عمودين.</h2> <ul> <li><span style="color:#e74c3c;">المعطيات:</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>▱</mo><mi>G</mi><mi>F</mi><mi>B</mi><mi>A</mi><mo> </mo><mo>,</mo><mo> </mo><mo>▱</mo><mi>H</mi><mi>A</mi><mi>C</mi><mi>D</mi></math></li> <li><span style="color:#e74c3c;">المطلوب:</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math></li> </ul> <p><img alt="شكل 19" src="https://saborah.net/app/webroot/upload/images/images/19(2).JPG" /></p> <p>الحل:</p> <p>البرهان: العبارات (المبررات):</p> <p>1) متوازيا الأضلاع GFBA، HACD (معطيات).</p> <p>2) <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>A</mi><mo> </mo><mo>,</mo><mo> </mo><mo>∠</mo><mi>A</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math> (الزوايا المتقابلة في متوازي الأضلاع متطابقة).</p> <p>3) <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo><mi>F</mi><mo> </mo><mo>≅</mo><mo> </mo><mo>∠</mo><mi>D</mi></math> (خاصية التعدي).</p> <h2>أوجد قيمتي x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع:</h2> <h2>20)</h2> <p><img alt="شكل 20" src="https://saborah.net/app/webroot/upload/images/images/20(2).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mi>x</mi><mo>+</mo><mn>5</mn><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi>x</mi><mo>−</mo><mi>x</mi><mo>=</mo><mn>5</mn><mo>−</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>+</mo><mn>10</mn><mo>=</mo><mn>2</mn><mi>y</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>10</mn><mo>−</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>5</mn></mtd></mtr></mtable></math></p> <h2>21)</h2> <p><img alt="شكل 21" src="https://saborah.net/app/webroot/upload/images/images/21(1).JPG" /></p> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>2</mn><mo>=</mo><mn>2</mn><mi>x</mi><mo>+</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>3</mn><mi>x</mi><mo>−</mo><mn>2</mn><mi>x</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>x</mi><mo>=</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>4</mn><mi>y</mi><mo>+</mo><mn>6</mn><mo>=</mo><mn>6</mn><mi>y</mi><mo>−</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>6</mn><mi>y</mi><mo>−</mo><mn>4</mn><mi>y</mi><mo>=</mo><mn>6</mn><mo>+</mo><mn>8</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mn>2</mn><mi>y</mi><mo>=</mo><mn>14</mn></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>7</mn></mtd></mtr></mtable></math></p> <h2>22)<span style="color:#e74c3c;"> طاولات: </span>لماذا يبقى سطح طاولة كي الثياب في الصورة أدناه موازياً لأرضية الغرفة دائماً؟</h2> <p><img alt="شكل 22" src="https://saborah.net/app/webroot/upload/images/images/طاولة.JPG" /></p> <p>الحل:</p> <p>عمل الساقان بحيث ينصف كل منهما الآخر اذن فالشكل الرباعي المتكون من أطراف الساقين يكون دائماً متوازي الأضلاع، لذلك فسطح الطاولة العلوي يبقى موازياً لسطح الأرض.</p> <h2>23) <span style="color:#e74c3c;">اختيار من متعدد:</span> أي الاشكال الرباعية الآتية ليس متوازي أضلاع؟</h2> <p>الحل:</p> <p><img alt="حل 23" src="https://saborah.net/app/webroot/upload/images/images/حل 23(1).JPG" /></p> <h2><span style="color:#e74c3c;">هندسة إحداثية:</span> حدد ما إذا كان الشكل الرباعي المعطاة إحداثيات رؤوسه في كل مما يأتي متوازي أضلاع. برر إجابتك باستعمال الطريقة المحددة في السؤال.</h2> <h2>24) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">A</mi><mo>(</mo><mo>-</mo><mn>6</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>5</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">B</mi><mo>(</mo><mo>-</mo><mn>1</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>4</mn><mo>)</mo><mo>,</mo><mo> </mo><mi mathvariant="normal">C</mi><mo>(</mo><mn>0</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>1</mn><mo>)</mo><mo>,</mo><mo> </mo><mi mathvariant="normal">D</mi><mo>(</mo><mo>-</mo><mn>5</mn><mo> </mo><mo>,</mo><mo> </mo><mo>-</mo><mn>2</mn><mo>)</mo></math> صيغة المسافة بين نقطتين.</h2> <p>الحل:</p> <p>نعم، يجب ان يكون كل ضلعين متقابلين متطابقين.</p> <ul> <li>المسافة بين A وB تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>26</mn></msqrt></math>. والمسافة بين B وC تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>10</mn></msqrt></math></li> <li>المسافة بين C وD تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>26</mn></msqrt></math>. والمسافة بين D وA تساوي <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><mn>10</mn></msqrt></math></li> </ul> <p>بما أن المسافة بين نقطتين تحسب من خلال <math xmlns="http://www.w3.org/1998/Math/MathML"><msqrt><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">x</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">x</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup><mo>+</mo><msup><mfenced separators="|"><mrow><msub><mi mathvariant="normal">y</mi><mn>2</mn></msub><mo>−</mo><msub><mi mathvariant="normal">y</mi><mn>1</mn></msub></mrow></mfenced><mn>2</mn></msup></msqrt></math></p> <p> </p> <h2>25) <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">Q</mi><mo>(</mo><mo>-</mo><mn>5</mn><mo> </mo><mo>,</mo><mo> </mo><mn>2</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">R</mi><mo>(</mo><mo>-</mo><mn>3</mn><mo> </mo><mo>,</mo><mo>-</mo><mn>6</mn><mo>)</mo><mo> </mo><mo>,</mo><mo> </mo><mi mathvariant="normal">S</mi><mo>(</mo><mn>2</mn><mo> </mo><mo>,</mo><mo> </mo><mn>2</mn><mo>)</mo><mo> </mo><mo>,</mo><mi mathvariant="normal">T</mi><mo>(</mo><mo>-</mo><mn>1</mn><mo> </mo><mo>,</mo><mo> </mo><mn>6</mn><mo>)</mo></math> صيغة الميل.</h2> <p>الحل:</p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em"><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>4</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn></mrow><mn>8</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn><mo>+</mo><mn>3</mn></mrow><mrow><mn>2</mn><mo>+</mo><mn>6</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>QR</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>5</mn></mrow><mrow><mo>−</mo><mn>8</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>3</mn><mo>−</mo><mn>2</mn></mrow><mrow><mo>−</mo><mn>6</mn><mo>−</mo><mn>2</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>RS</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mn>3</mn><mrow><mo>−</mo><mn>4</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>2</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>2</mn><mo>−</mo><mn>6</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>ST</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr><mtr><mtd><mfrac><mrow><mo>−</mo><mn>1</mn></mrow><mn>5</mn></mfrac><mo>=</mo><mfrac><mrow><mo>−</mo><mn>2</mn><mo>+</mo><mn>1</mn></mrow><mrow><mn>4</mn><mo>+</mo><mn>1</mn></mrow></mfrac><mo>:</mo><mover accent="true"><mi>OT</mi><mo accent="false">¯</mo></mover><mo> </mo><mi>ميل</mi></mtd></mtr><mtr><mtd></mtd></mtr></mtable></math></p> <p>بما أن ميل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>Q</mi><mi>R</mi></mrow><mo>¯</mo></mover></math> لا يساوي مبل <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>S</mi><mi>T</mi></mrow><mo>¯</mo></mover></math> ,فإن QRST ليس متوازي أضلاع.</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '751', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ), (int) 5 => array( 'Nodetext' => array( 'slug' => 'الدرس_الرابع_المستطيل', 'title' => 'الدرس الرابع: المستطيل', 'title_seo' => 'حل درس المستطيل - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '754', 'thumb' => null, 'parentID' => '472', 'sequence' => '4', 'has_videos' => '1' ) ), (int) 6 => array( 'Nodetext' => array( 'slug' => 'الدرس_الخامس_المعين_والمربع', 'title' => 'الدرس الخامس: المعين والمربع', 'title_seo' => 'حل درس المعين والمربع - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '787', 'thumb' => null, 'parentID' => '472', 'sequence' => '5', 'has_videos' => '1' ) ), (int) 7 => array( 'Nodetext' => array( 'slug' => 'الدرس_السادس_شبه_المنحرف_وشكل_الطائرة_الورقية', 'title' => 'الدرس السادس: شبه المنحرف وشكل الطائرة الورقية', 'title_seo' => 'حل درس شبه المنحرف وشكل الطائرة الورقية - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '806', 'thumb' => null, 'parentID' => '472', 'sequence' => '6', 'has_videos' => '1' ) ), (int) 8 => array( 'Nodetext' => array( 'slug' => 'دليل_الدراسة_والمراجعة', 'title' => 'دليل الدراسة والمراجعة', 'title_seo' => 'حل اسئلة دليل الدراسة والمراجعة - رياضيات 2 ثانوي مقررات', 'content' => '', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '7708', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ), (int) 9 => array( 'Nodetext' => array( 'slug' => 'الإعداد_للاختبارات', 'title' => 'الإعداد للاختبارات', 'title_seo' => null, 'content' => '<h2><img alt="الإعداد للإختبار" src="https://saborah.net/app/webroot/upload/images/images/1(2323).JPG" /><img alt="تمارين ومسائل" src="https://saborah.net/app/webroot/upload/images/images/تمارين ومسائل(7).JPG" /></h2> <h2>اقرأ كل مسألة مما يأتي، وحدّد المطلوب، ثم استعمل المعطيات لحلها، وبيّن خطوات حلك:</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>R</mi><mi>S</mi></mrow><mo>¯</mo></mover></math> قطعة متوسطة لشبه المنحرف MNOP. ما طول <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>R</mi><mi>S</mi></mrow><mo>¯</mo></mover></math>؟</h2> <p><img alt="شبه منحرف" src="https://saborah.net/app/webroot/upload/images/images/1(2324).JPG" /></p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mi>RS</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mi>MN</mi><mo>+</mo><mi>PO</mi><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mn>9</mn><mi mathvariant="normal">x</mi><mo>−</mo><mn>1</mn><mo>)</mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>10</mn><mi>x</mi><mo>+</mo><mn>3</mn><mo>+</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>7</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mo>(</mo><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>)</mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>14</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>=</mo><mn>7</mn><mi>x</mi><mo>+</mo><mn>5</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>9</mn><mi>x</mi><mo>−</mo><mn>7</mn><mi>x</mi><mo>=</mo><mn>5</mn><mo>+</mo><mn>1</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>2</mn><mi>x</mi><mo>=</mo><mn>6</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>R</mi><mi>S</mi><mo>=</mo><mn>9</mn><mi>x</mi><mo>−</mo><mn>1</mn><mo>=</mo><mn>27</mn><mo>−</mo><mn>1</mn><mo>=</mo><mn>26</mn></mtd></mtr></mtable></math></p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>A</mi><mi>B</mi></mrow><mo accent="false">¯</mo></mover><mo>∥</mo><mover><mrow><mi>D</mi><mi>C</mi></mrow><mo accent="false">¯</mo></mover></math>، فأوجد قيمة x.</h2> <p><img alt="متوازي الأضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2325).JPG" /></p> <p><span style="color:#27ae60;">j=115</span></p> <p><span style="color:#27ae60;">x+65=180</span></p> <p><span style="color:#27ae60;">x=180-65</span></p> <p><span style="color:#27ae60;">x=115</span></p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> استعن بالتمثيل البياني أدناه في كل من السؤالين الآتيين:</h2> <p><img alt="التمثيل البياني" src="https://saborah.net/app/webroot/upload/images/images/1(2326).JPG" /></p> <h2>a) هل ينصف قطرا الشكل الرباعي RSTU كل منهما الآخر؟ استعمل صيغة المسافة بين نقطتين لتتحقق من إجابتك.</h2> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right" columnspacing="1em" mathcolor="#007F00"><mtr><mtd><mi mathvariant="normal">S</mi><mo>(</mo><mn>5</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi>P</mi><mo>(</mo><mn>0</mn><mo>,</mo><mo>−</mo><mn>1</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">R</mi><mo>(</mo><mo>−</mo><mn>3</mn><mo>,</mo><mn>2</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">U</mi><mo>(</mo><mo>−</mo><mn>5</mn><mo>,</mo><mo>−</mo><mn>4</mn><mo>)</mo><mo>,</mo><mi mathvariant="normal">T</mi><mo>(</mo><mo>−</mo><mn>3</mn><mo>,</mo><mo>−</mo><mn>4</mn><mo>)</mo></mtd></mtr><mtr><mtd><mi>RP</mi><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>−</mo><mn>2</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>18</mn></msqrt></mtd></mtr><mtr><mtd><mi>P</mi><mi>T</mi><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>3</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>18</mn></msqrt></mtd></mtr><mtr><mtd><mtext>PS</mtext><mo>=</mo><msqrt><mo>(</mo><mn>5</mn><mo>−</mo><mn>0</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mn>2</mn><mo>+</mo><mn>1</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>34</mn></msqrt></mtd></mtr><mtr><mtd><mtext>UP</mtext><mo>=</mo><msqrt><mo>(</mo><mn>0</mn><mo>+</mo><mn>5</mn><msup><mo>)</mo><mn>2</mn></msup><mo>+</mo><mo>(</mo><mo>−</mo><mn>1</mn><mo>+</mo><mn>4</mn><msup><mo>)</mo><mn>2</mn></msup></msqrt><mo>=</mo><msqrt><mn>34</mn></msqrt></mtd></mtr></mtable></math></p> <p><span style="color:#27ae60;">بما أن <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">UP</mi><mo mathcolor="#007F00">=</mo><msqrt mathcolor="#007F00"><mn>34</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">PS</mi><mo mathcolor="#007F00">=</mo><msqrt mathcolor="#007F00"><mn>34</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">PT</mi><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">3</mn><msqrt mathcolor="#007F00"><mn>2</mn></msqrt><mo mathcolor="#007F00">,</mo><mi mathcolor="#007F00">RP</mi><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">3</mn><msqrt mathcolor="#007F00"><mn>2</mn></msqrt></math>، فإن القطران ينصف كل منهما الآخر.</span></p> <h2>b) ما نوع الشكل الرباعي RSTU؟ وضح إجابتك باستعمال خصائص هذا النوع من الأشكال الرباعية أو تعريفه.</h2> <p>متوازي أضلاع، إذا كان قطرا شكل رباعي ينصف كل منهما الآخر فإن الشكل متوازي أضلاع.</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">4)</span></span> ما مجموع قياسات الزوايا الخارجية للثماني المنتظم؟</h2> <p>ْ360</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '7879', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '-1' ) ), (int) 10 => array( 'Nodetext' => array( 'slug' => 'اختبار_تراكمي', 'title' => 'اختبار تراكمي', 'title_seo' => null, 'content' => '<h2><img alt="اختبار تراكمي" src="https://saborah.net/app/webroot/upload/images/images/1(2327).JPG" /></h2> <h2><img alt="الاختيار من متعدد" src="https://saborah.net/app/webroot/upload/images/images/1(2334).JPG" /></h2> <h2>اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة.</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">1)</span></span> إذا كان <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo>∥</mo><mi>b</mi></math>، فأي العبارات الآتية ليست صحيحة؟</h2> <p><img alt="اختبار تراكمي" src="https://saborah.net/app/webroot/upload/images/images/1(2328).JPG" /></p> <ul> <li><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi mathvariant="normal">∠</mi><mn>1</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>3</mn></mtd></mtr></mtable></math></li> <li><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathvariant="normal">∠</mi><mn>4</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>7</mn></math></li> <li><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em"><mtr><mtd></mtd><mtd><mi mathvariant="normal">∠</mi><mn>2</mn><mo>≅</mo><mi mathvariant="normal">∠</mi><mn>5</mn></mtd></mtr></mtable></math></li> <li><math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00" mathvariant="normal">∠</mi><mn mathcolor="#007F00">8</mn><mo mathcolor="#007F00">≅</mo><mi mathcolor="#007F00" mathvariant="normal">∠</mi><mn mathcolor="#007F00">2</mn></math></li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">2)</span></span> صنّف المثلث أدناه تبعاً لقياسات زواياه، اختر المصطلح الأنسب.</h2> <p><img alt="مثلث" src="https://saborah.net/app/webroot/upload/images/images/1(2329).JPG" /></p> <ul> <li>حاد الزوايا.</li> <li><strong><span style="color:#27ae60;">متطابق الزوايا.</span></strong></li> <li>منفرج الزاوية.</li> <li>قائم الزاوية.</li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">3)</span></span> أوجد قيمة x في متوازي الأضلاع RSTU.</h2> <p><img alt="متوازي الأضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2330).JPG" /></p> <ul> <li>12</li> <li>18</li> <li>25</li> <li><strong><span style="color:#27ae60;">30</span></strong></li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">4)</span></span> ما قياس كل زاوية داخلية في الخماسي المنتظم؟</h2> <p><img alt="خماسي" src="https://saborah.net/app/webroot/upload/images/images/1(2331).JPG" /></p> <ul> <li>ْ96</li> <li><span style="color:#27ae60;">ْ<strong>108</strong></span></li> <li>ْ120</li> <li>ْ135</li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">5)</span></span> الشكل الرباعي ABCD معين، فيه ° m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo></math>BCD = 120، أوجد m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>∠</mo></math>DAC.</h2> <p><img alt="الشكل الرباعي" src="https://saborah.net/app/webroot/upload/images/images/1(2332).JPG" /></p> <ul> <li>ْ30</li> <li><span style="color:#27ae60;">ْ<strong>60</strong></span></li> <li>ْ90</li> <li>ْ120</li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">6)</span></span> ما قيمة x في الشكل أدناه؟</h2> <p><img alt="تقاطع" src="https://saborah.net/app/webroot/upload/images/images/1(2333).JPG" /></p> <ul> <li>10</li> <li><strong><span style="color:#27ae60;">12</span></strong></li> <li>14</li> <li>15</li> </ul> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">7)</span></span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mrow><mi>D</mi><mi>T</mi></mrow><mo accent="false">¯</mo></mover><mo>,</mo><mover><mrow><mi>A</mi><mi>E</mi></mrow><mo accent="false">¯</mo></mover></math> قطران للمستطيل DATE يتقاطعان في S، إذا كان AE=40, ST=x+5، فما قيمة x؟</h2> <ul> <li>35</li> <li>25</li> <li><strong><span style="color:#27ae60;">15</span></strong></li> <li>10</li> </ul> <h2><img alt="إجابات قصيرة" src="https://saborah.net/app/webroot/upload/images/images/1(2335).JPG" /></h2> <h2>اكتب إجابتك في ورقة الإجابة.</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">8)</span></span> تشكّل أعمدة خيمة رؤوس سداسي منتظم، ما قياس الزاوية المتكونة عند أي من أركان الخيمة؟</h2> <p><img alt="خسمة" src="https://saborah.net/app/webroot/upload/images/images/1(2336).JPG" /></p> <p><span style="color:#27ae60;">G=ْ120</span></p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mo>(</mo><mi>n</mi><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><mo>(</mo><mn>6</mn><mo>−</mo><mn>2</mn><mo>)</mo><mo>⋅</mo><mn>180</mn><mo>=</mo><msup><mn>720</mn><mo>∘</mo></msup></mtd></mtr><mtr><mtd></mtd><mtd><mo>=</mo><mfrac><mn>720</mn><mn>6</mn></mfrac><mo>=</mo><msup><mn>120</mn><mo>∘</mo></msup></mtd></mtr></mtable></math></p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">9)</span></span> ما إحداثيات الرأس الرابع لشبه المنحرف المتطابق الساقين LMNJ؟ بين خطوات الحل.</h2> <p><img alt="رؤوس شبه منحرف متطابق الساقين" src="https://saborah.net/app/webroot/upload/images/images/1(2337).JPG" /></p> <p><span style="color:#27ae60;">(-6,3)</span></p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">10)</span></span> ماذا نسمي متوازي الأضلاع إذا كان قطراه متعامدين؟ وضح إجابتك.</h2> <p>يكون مربعاً أو معيناً.</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">11)</span></span> حدّد ما إذا كانت النتيجة صحيحة أم لا فيما يأتي اعتماداً على المعطيات، فسّر تبريرك.</h2> <h2><span style="color:#e74c3c;">المعطيات: </span>إذا كان العدد يقبل القسمة على 9، فإنه يقبل القسمة على 3.<br /> العدد 144 يقبل القسمة على 9.</h2> <h2><span style="color:#e74c3c;">النتيجة:</span><strong> </strong>العدد 144 يقبل القسمة على 3.</h2> <p>النتيجة صحيحة: قانون الفصل المنطقي.</p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">12)</span></span> أوجد قيمة x في الشكل أدناه، وقرب الإجابة إلى أقرب عشر إن كان ذلك ضرورياً.</h2> <p><img alt="شبه منحرف" src="https://saborah.net/app/webroot/upload/images/images/1(2338).JPG" /></p> <p><math xmlns="http://www.w3.org/1998/Math/MathML"><mtable columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" mathcolor="#007F00"><mtr><mtd></mtd><mtd><mn>5</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>10</mn><mi>x</mi><mo>−</mo><mn>2</mn><mo>+</mo><mn>6</mn><mi>x</mi><mo>+</mo><mn>4</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>5</mn><mi>x</mi><mo>+</mo><mn>10</mn><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>(</mo><mn>16</mn><mi>x</mi><mo>+</mo><mn>2</mn><mo>)</mo></mtd></mtr><mtr><mtd></mtd><mtd><mn>10</mn><mi>x</mi><mo>+</mo><mn>20</mn><mo>=</mo><mn>16</mn><mi>x</mi><mo>+</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>16</mn><mi>x</mi><mo>−</mo><mn>10</mn><mi>x</mi><mo>=</mo><mn>20</mn><mo>−</mo><mn>2</mn></mtd></mtr><mtr><mtd></mtd><mtd><mn>6</mn><mi>x</mi><mo>=</mo><mn>18</mn></mtd></mtr><mtr><mtd></mtd><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr></mtable></math></p> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">13)</span></span> ما إحداثيات مركز الدائرة التي تمر برؤوس المثلث أدناه؟</h2> <p><img alt="التمثيل البياني" src="https://saborah.net/app/webroot/upload/images/images/1(2339).JPG" /></p> <p>رؤوس المثلث هي (0,0)(2,0)(0,4).</p> <p>معادلة أحد الأعمدة المنصفة هي <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">y</mi><mo mathcolor="#007F00">=</mo><mfrac mathcolor="#007F00"><mrow><mn>2</mn><mo>−</mo><mn>0</mn></mrow><mn>2</mn></mfrac><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">1</mn></math> ومعادلة عمود منصف آخر هي <math xmlns="http://www.w3.org/1998/Math/MathML"><mi mathcolor="#007F00">x</mi><mo mathcolor="#007F00">=</mo><mfrac mathcolor="#007F00"><mrow><mn>4</mn><mo>−</mo><mn>0</mn></mrow><mn>2</mn></mfrac><mo mathcolor="#007F00">=</mo><mn mathcolor="#007F00">2</mn></math>. ويتقاطع هذان العمودان عند النقطة (5,3) لذلك مرز الدائرة التي تمر في رؤوس المثلث يقع عند النقطة (1,2).</p> <h2><img alt="إجابات مطولة" src="https://saborah.net/app/webroot/upload/images/images/1(2340).JPG" /></h2> <h2>اكتب إجابتك في ورقة الإجابة مبيناً خطوات الحل.</h2> <h2><span style="color:#ffffff;"><span style="background-color:#e74c3c;">14)</span></span> هل يمكنك إثبات أن كل شكل مما يأتي متوازي أضلاع؟ إذا لم تستطع ذلك، فاذكر المعطيات الإضافية التي ستحتاج إليها لإثبات أنه متوازي أضلاع، ووضح تبريرك.</h2> <h2>a)</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2341).JPG" /></p> <p>نعم، الأضلاع المتقابلة متطابقة، لذا فالشكل متوازي أضلاع.</p> <h2>b)</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2342).JPG" /></p> <p>لا، ضلعان متقابلان فقط متوازيان عليك أن تبين أن:</p> <ul> <li>الضلعان المتوازيان متطابقان أيضاً.</li> <li>الضلعان المتقابلان الآخران متوازيان.</li> </ul> <h2>c)</h2> <p><img alt="متوازي أضلاع" src="https://saborah.net/app/webroot/upload/images/images/1(2343).JPG" /></p> <p>نعم، الزوايا المتقابلة متطابقة لذا فالشكل متوازي أضلاع.</p> ', 'desc' => '', 'tags' => null ), 'Node' => array( 'id' => '7890', 'thumb' => null, 'parentID' => '472', 'sequence' => '0', 'has_videos' => '1' ) ) ) $exams = array( (int) 0 => array( 'id' => '1621', 'title' => 'اختبار الكتروني: اختبار الفصل', 'questions' => null, 'percent' => (float) NAN ) ) $videos = array( (int) 0 => array( 'Nodegallery' => array( 'filename' => 'i45E0Q3etrs', 'id' => '2536' ), 'Nodegallerytext' => array( 'title' => 'فيديو حل اختبار الفصل' ) ), (int) 1 => array( 'Nodegallery' => array( 'filename' => 'msrnKmGq9mM', 'id' => '2537' ), 'Nodegallerytext' => array( 'title' => 'فيديو حل اختبار الفصل' ) ), (int) 2 => array( 'Nodegallery' => array( 'filename' => 'pH1LGhyqYY8', 'id' => '2538' ), 'Nodegallerytext' => array( 'title' => 'فيديو حل اختبار الفصل' ) ) ) $comments = array() $news = array( (int) 0 => array( 'Item' => array( 'id' => '6', 'thumb' => '1644261984.jpg' ), 'Itemtext' => array( 'name' => ' 50 الف طالب كوري يدرسون اللغة العربية في كوريا الجنوبية' ) ), (int) 1 => array( 'Item' => array( 'id' => '8', 'thumb' => '1644262073.jpg' ), 'Itemtext' => array( 'name' => ' الشقيقان السعوديان دعاء وضياء يتصدران عباقرة العالم في الرياضيات' ) ), (int) 2 => array( 'Item' => array( 'id' => '7', 'thumb' => '1644262036.jpg' ), 'Itemtext' => array( 'name' => ' وزير التعليم يفتتح مبنى الملحقية الثقافية في ماليزيا ويلتقي الطلبة المبتعثين' ) ) ) $BANNERS = array( 'home-classes-up' => array( 'Zone' => array( 'adsZID' => '1', 'zoneName' => 'home-classes-up', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'home-classes-down' => array( 'Zone' => array( 'adsZID' => '2', 'zoneName' => 'home-classes-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'articles-down' => array( 'Zone' => array( 'adsZID' => '3', 'zoneName' => 'articles-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'lesson-up' => array( 'Zone' => array( 'adsZID' => '4', 'zoneName' => 'lesson-up', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'level-up' => array( 'Zone' => array( 'adsZID' => '5', 'zoneName' => 'level-up', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'lesson-down' => array( 'Zone' => array( 'adsZID' => '8', 'zoneName' => 'lesson-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array( 'Adsbanner' => array( [maximum depth reached] ) ) ), 'level-down' => array( 'Zone' => array( 'adsZID' => '9', 'zoneName' => 'level-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'related-lessons' => array( 'Zone' => array( 'adsZID' => '10', 'zoneName' => 'related-lessons', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'article-up' => array( 'Zone' => array( 'adsZID' => '11', 'zoneName' => 'article-up', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'article-down' => array( 'Zone' => array( 'adsZID' => '12', 'zoneName' => 'article-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'question-up' => array( 'Zone' => array( 'adsZID' => '13', 'zoneName' => 'question-up', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'question-down' => array( 'Zone' => array( 'adsZID' => '14', 'zoneName' => 'question-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ), 'question-lesson-down' => array( 'Zone' => array( 'adsZID' => '15', 'zoneName' => 'question-lesson-down', 'isMultiAds' => '-1', 'zoneBreak' => null, 'isRand' => '-1' ), 'Banner' => array() ) ) $_privilege = array() $_menus = array() $_nodes = array() $_contactus = array() $_banners = array() $_pages = array() $_langs = array( (int) 0 => array( 'Lang' => array( 'id' => 'ara', 'language' => 'Arabic' ) ) ) $request_count = (int) 998 $socical_networks = array( (int) 0 => array( 'Confdb' => array( 'key' => 'twitter', 'value' => '#' ) ), (int) 1 => array( 'Confdb' => array( 'key' => 'youtube', 'value' => '#' ) ), (int) 2 => array( 'Confdb' => array( 'key' => 'linkedin', 'value' => '#' ) ) ) $_Language = array( 'ara' => 'Arabic' ) $Config = array( 'name_eng' => 'Saborah', 'name_ara' => 'موقع سبورة - طلاب السعودية', 'from' => 'سبورة', 'fromaddress' => 'noreply@saborah.net', 'email_monitor' => 'info@saborah.net', 'listrow' => '12', 'url' => 'https://saborah.net', 'email_formname' => 'سبورة', 'facebook' => '', 'twitter' => '#', 'youtube' => '#', 'linkedin' => '#', 'phone' => '', 'time_format' => 'H:i A', 'node_sep_slug' => '_', 'latest_update_website' => '2022-12-02 14:25:47', 'latest_login_admin' => '2022-03-16 06:26:54', 'google_secret_key' => '6LcBYhUTAAAAABPinPa4vlhvDuhne95ZnfUao0tw', 'site_key' => '6LcBYhUTAAAAAIurIcmwQzN4C2kkYLYBHyGxKWzO', 'map' => '31.99415,35.870693', 'map_center' => '31.99415,35.870693', 'keywords_ara' => 'حلول, حل, إجابات, إجابة, علوم, رياضيات, فقه, لغة, عربية, متوسط, ثانوي, الفصل, الأول, الثاني, مواد, دراسة, واجبي', 'description_ara' => 'حل الواجبات المدرسية لطلاب السعودية ف1 ف2 وجميع المواد والصفوف الدراسية من رياضيات وعلوم واجتماعيات وفقه وحاسوب', 'instagram' => '', 'admin_email' => 'mkhuder@gmail.com', 'map_zoom' => '14', 'header_code' => '<!-- Google tag (gtag.js) --> <script async src="https://www.googletagmanager.com/gtag/js?id=UA-216508974-1"></script> <script> window.dataLayer = window.dataLayer || []; function gtag(){dataLayer.push(arguments);} gtag('js', new Date()); gtag('config', 'UA-216508974-1'); </script> <!-- <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script> --> <link rel="manifest" href="/manifest.json" > <script> const appId = "95217417-b5c7-42eb-ada0-f01acc0ba857"; const auto_register = true; //write your tags as json format //const tags = '{"key1":"value1", "key2":"value2"}'; </script> <script src="https://pushtiger.com/settings.js" ></script>', 'body_code' => '', 'website_author' => 'Sama IT Solution', 'dashboard_url' => '/admin/node/index', 'admin-panel-url' => 'backdoor', 'admin-theme-color' => '3994C7', 'email_format' => '[^@]+@[^@]+.[a-zA-Z]{2,6}', 'password_format' => '.{6,}', 'keywords_eng' => '', 'description_eng' => '', 'google-map-api-key' => 'AIzaSyBb71HgSD8EiowFnx3HRBa5pw96ChhJeMU', 'max-char-node-url' => '58', 'default-color' => '1075a9', 'api-key' => '317bbb', 'apiKey' => 'AIzaSyDQGQ05rKO5otB4_EqLW-oboBIgdDLBAUQ', 'authDomain' => 'saborah-f5614.firebaseapp.com', 'databaseURL' => 'https://saborah-f5614-default-rtdb.europe-west1.firebasedatabase.app', 'user-offline-after' => '1', 'service_account' => 'saborah-f5614-b95c91e5ec9f.json', 'thumb_width' => '400', 'min-nodes-count-view-news' => '4', 'name_default_ara' => 'سبورة', 'google-api-notification-key' => 'AAAAP5FT_i8:APA91bGmsp2e-BgVYKUO58Su2zlMp3qX6aynA4flPYpjjYEOrMD1A7zeRuC4YxVg254PcbFquFOdHKOAm5WKPyQh2wzwBVe_3HB9TSxoRokeGD21LWD4Q3wj8WShkGcEsx6iFQkqehlM', 'app-package-names' => 'net.saborah.app,net.saborah.app.fifth,net.saborah.app.sixth,net.saborah.app.seventh,net.saborah.app.eighth,net.saborah.app.ninth,net.saborah.app.thanwya,net.saborah.app.third,net.saborah.app.fourth', 'user-new-type' => '100', 'user-active-type' => '200', 'user-special-type' => '300', 'header_code_inside' => '<script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>', 'google-play-app' => 'https://play.google.com/store/apps/details?id=net.saborah.app', 'header_code_inside_question' => ' <script async src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js?client=ca-pub-6671772191390777" crossorigin="anonymous"></script>', 'Languages' => null ) $headline = 'الاختبارات' $data = array( 'id' => '1621', 'title' => 'اختبار الكتروني: اختبار الفصل', 'questions' => null, 'percent' => (float) NAN )include - APP/View/Elements/lesson/exams.ctp, line 20 View::_evaluate() - CORE/Cake/View/View.php, line 971 View::_render() - CORE/Cake/View/View.php, line 933 View::_renderElement() - CORE/Cake/View/View.php, line 1224 View::element() - CORE/Cake/View/View.php, line 418 include - APP/View/Node/lesson.ctp, line 3 View::_evaluate() - CORE/Cake/View/View.php, line 971 View::_render() - CORE/Cake/View/View.php, line 933 View::render() - CORE/Cake/View/View.php, line 473 Controller::render() - CORE/Cake/Controller/Controller.php, line 968 NodeController::index() - APP/Controller/NodeController.php, line 263 ReflectionMethod::invokeArgs() - [internal], line ?? Controller::invokeAction() - CORE/Cake/Controller/Controller.php, line 499 Dispatcher::_invoke() - CORE/Cake/Routing/Dispatcher.php, line 193 Dispatcher::dispatch() - CORE/Cake/Routing/Dispatcher.php, line 167 [main] - APP/webroot/index.php, line 108
اختبار الفصل
أوجد مجموع قياسات الزوايا الداخلية في كل من المضلعين المحدبين الآتيين:
1) السداسي.
n=6
720°=180°.(4)=180°.(6-2)=180°.(n-2)
2) ذو 16 ضلعاً.
n=16
2520°=180°.(14)=180°.(16-2)=180°.(n-2)
3) فن: تصنع جمانة إطاراً لتبسط عليه قطعة قماش وترسم عليها بألوان زيتية، ثبتت جمانة أربع قطع من الخشب بعضها ببعض
واعتقدت أنها ستمثل مربعاً.
a) كيف يمكنها التحقق من أن الإطار مربع؟
إذا كانت الزوايا الأربعة قائمة فإن الشكل مستطيل، وإذا كانت الأضلاع المتتالية متطابقة فإن الشكل معين، وحسب النظرية 1.20 بما أن الشكل مستطيل ومعين فإنه مربع.
b) إذا كانت أبعاد الإطار كما في الشكل، فأوجد القياسات المجهولة.
بما أن أضلاع المربع الأربعة متساوية الطول فإن x=2 ft
وبما أن زوايا المربع الأربعة قائمة فإن y=90°
الشكل الرباعي ABCD شبه منحرف متطابق الساقين.
4) ما الزاوية التي تطابق ؟
حسب النظرية 1.21 إذا كان شبه المنحرف متطابق الساقين، فإن زاويتي كل قاعدة متطابقتان.
5) ما الضلع الذي يوازي ؟
حسب تعريف شبه المنحرف يكون:
6) ما القطعة المستقيمة التي تطابق ؟
حسب نظرية 1.23 يكون شبه المنحرف متطابق الساقين، إذا وفقط إذا كان قطراه متطابقين.
وبالتالي فإن:
أوجد عدد أضلاع المضلع المنتظم المعطى مجموع قياسات زواياه في كل مما يأتي:
7) 900
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 900 هو حل المعادلة:
بما أن n=7 إذاً للمضلع 7 أضلاع.
8) 1890
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 1890 هو حل المعادلة:
بما أن n=13 إذاً للمضلع 13 ضلع.
9) 2880
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 2880 هو حل المعادلة:
بما أن n=18 إذاً للمضلع 18 ضلع.
10) 5400
عدد أضلاع المضلع الذي مجموع قياس زواياه الداخلية 5400 هو حل المعادلة:
بما أن n=32 إذاً للمضلع 32 ضلع.
11) اختيار من متعدد: إذا كان QRST متوازي الأضلاع، فما قيمة x؟
- 11
- 12
- 13
- 14
إذا كان CDFG على شكل طائرة ورقية فأوجد القياس المطلوب في كل من السؤالين الآتيين:
12) GF
بما أن قطري شكل الطائرة الورقية متعامدان فإنهما يقسمانه إلى أربعة مثلثات قائمة الزاوية.
نستعمل نظرية فيثاغورس لإيجاد GF:
13)
بما أن الشكل طائرة ورقية فإنه حسب النظرية 1.26 يكون ، وبما أن الطائرة الورقية لها أربعة أضلاع، فإن مجموع قياسات زواياه الداخلية 360:
جبر: استعن بالمعين MNOP للإجابة عن الأسئلة الآتية:
14)
بما أن قطرا المعين متعامدان فإن المثلث قائم وبالتالي فإن:
15) إذا كان 12 = PR، فأوجد RN.
قطرا المعين ينصف كل منهما الآخر: RN=PR=12
16) إذا كان 124 = ، فأوجد .
كل قطر في المعين ينصف الزاويتين اللتين يصل بين رأسيهما وبالتالي:
17) إنشاءات: تبني عائلة صالح ملحقاً للمنزل، وتركت فتحة لنافذة جديدة. فإذا قاس صالح الأضلاع المتقابلة فوجدها متطابقة. وقاس القطرين فوجدهما متطابقين، فهل يمكنه القول: إن فتحة النافذة تمثل مستطيلاً؟ وضح إجابتك.
نعم فتحة النافذة تمثل مستطيلاً، في الشكل الرباعي إذا كان كل ضلعين متقابلين متطابقان فإن الشكل الرباعي متوازي أضلاع، وإذا كان قطرا متوازي الأضلاع متطابقان فإنه مستطيل.
استعمل المبين جانباً لإيجاد كل مما يأتي:
18)
كل زاويتين متقابلتين في متوازي الأضلاع متطابقتان (النظرية 1.4)
19) JK
كل ضلعين متقابلين في متوازي الأضلاع متطابقان (النظرية 1.3)
JK=ML=6
20)
كل زاويتين متحالفتين في متوازي الأضلاع متكاملتان (النظرية 1.5)
جبر: استعن بالمستطيل DEFG للإجابة عن الأسئلة التالية:
21) إذا كان ، فاوجد EG.
لإيجاد EG نوجد قيمة x:
لحساب EG نعوض قيمة x=9:
22) إذا كان ، فأوجد .
نوجد قيمة x:
نعوض قيمة x=5:
23) إذا كان ، فأوجد GF.
نوجد قيمة x:
نعوض قيمة x=10:
حدد ما إذا كان الشكل الرباعي متوازي أضلاع أم لا في كل مما يأتي. برر إجابتك.
24) .JPG)
نعم الشكل الرباعي متوازي أضلاع لأن كل زاويتين متقابلتين متطابقتان. (النظرية 1.9)
25) 
الشكل الرباعي ليس متوازي أضلاع لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.

.JPG)
.JPG)
.JPG)
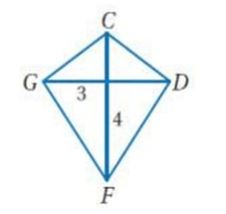
.JPG)
.JPG)
.JPG)
.JPG)




النقاشات