توسع التكبير والتصغير

حلل النتائج:

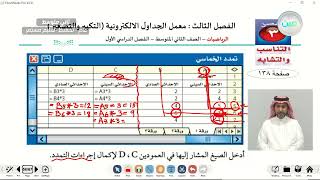
١) كيف تستعمل الصيغة الواردة في العمودين D ،C لتغيير المضلع الخماسي الأصلي؟ وضح إجابتك.

استعمل بالتعويض عن قيمة A وB حيث تعبر هذه الصيغة الواردة في العمودين D، C عن تمديد المضلع الخماسي بضرب كل من الإحداثي السيني والصادي لنقاطه بعامل المقياس (٣).

٢) مثل بيانياً المضلع الخماسي الأصلي وتمدده على ورقة مربعات.

إحداثيات الخماسي الجديد:

(٦، ٦)، (١٢، ٦)، (١٥، ١٢)، (٩، ١٨)، (٣، ١٢)

٣) ما النسبة المئوية لمقدار الزيادة في الشكل الناتج عن التمدد مقارنة بالشكل الأصلي؟

عامل مقياس التمدد = $\frac{\mathrm{٣}}{\mathrm{١}}=\frac{س}{\mathrm{١٠٠}}\leftarrow$ س = ٣٠٠ $\leftarrow$ النسبة المئوية لمقدار الزيادة هو ٣٠٠٪.

٤) أوجد إحداثيات رؤوس المضلع الخماسي بعد تكبيره خمس مرات.

الإحداثيات بعد التكبير ٥ مرات هي:

• (٢، ٢) $\leftarrow$ (٢ × ٥، ٢× ٥) $\leftarrow$ (١٠، ١٠).
• (٤، ٢) $\leftarrow$ (٤ × ٥، ٢× ٥) $\leftarrow$ (٢٠، ١٠).
• (٥، ٤) $\leftarrow$ (٥ × ٥، ٤× ٥) $\leftarrow$ (٢٥، ٢٠).
• (٣، ٦) $\leftarrow$ (٣ × ٥، ٦× ٥) $\leftarrow$ (١٥، ٣٠).
• (١، ٤) $\leftarrow$ (١ × ٥، ٤× ٥) $\leftarrow$ (٥، ٢٠).

٥ ) أوجد إحداثيات رؤوس المضلع الخماسي بعد تصغيره نصف مرة.

الإحداثيات بعد التصغير $\frac{\mathrm{١}}{\mathrm{٢}}$ مرات هي:

• (٢، ٢) $\leftarrow$ (٢ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ (١، ١).
• (٤، ٢) $\leftarrow$ (٤ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٢× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ (٢، ١).
• (٥، ٤) $\leftarrow$ (٥ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ (٢,٥، ٢).
• (٣، ٦) $\leftarrow$ (٣ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٦× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ (١,٥، ٣).
• (١، ٤) $\leftarrow$ (١ × $\frac{\mathrm{١}}{\mathrm{٢}}$، ٤× $\frac{\mathrm{١}}{\mathrm{٢}}$) $\leftarrow$ ($\frac{\mathrm{١}}{\mathrm{٢}}$، ٢).

٦) خمن: ما نوع التمدد إذا كانت إحداثيات رؤوس المضلع الخماسي الجديدة كما يلي: (٥، ٥)، (١٠، ٥)، (٥، ١٢، ١٠)، (٥، ٧، ١٥)، (٥، ٢، ١٠)؟ وما قيمة عامل المقياس؟

نلاحظ أن جميع إحداثيات الشكل الجديد أكبر من نظيراتها في الشكل الأصلي $\leftarrow$ التمديد تكبير.

عامل مقياس التمدد = $\frac{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{لنقطة} \mathrm{من} \mathrm{الخماسي} \mathrm{الجديد}}{\mathrm{الإحداثي} \mathrm{السيني} \mathrm{لنظيراتها} \mathrm{من} \mathrm{الخماسي} \mathrm{الأصلي}}=\frac{\mathrm{٥}}{\mathrm{٢}}$ = ٢,٥

بما أن عامل مقياس التمدد = ٢,٥ > ١ فإن التمدد تكبير.

٧) اختر شكلاً هندسياً آخر، وعين نقاطه على ورقة مربعات، استعمل برنامج الجداول الإلكترونية لإيجاد تمددين له، أحدهما تكبير، والآخر تصغير.

نشاط عملي يحله الطالب مستخدماً برنامج الإكسل وللتكبير ويضرب إحداثيي كل نقطة بعدد > ١ وللتصغير يضرب إحداثيي كل نقطة بعدد < ١.