حل أسئلة تدرب وحل المسائل
جبر: أوجد قيمة x في كل مما يأتي:
7)
بما أن الأوتار متطابقة إذاً الأقواس المقابلة لها متطابقة:
8)
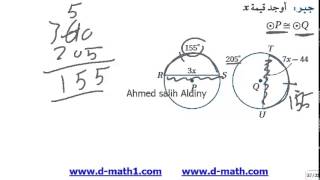
9)
بما أن الأوتار متطابقة إذاً الأقواس المقابلة لها متطابقة:
10)
11)
إذا كان طول نصف قطر يساوي 14 و CD=22، فأوجد القياسين الآتيين مقرباً إجابتك إلى أقرب جزء من مئة، إذا لزم ذلك.
12) CE
13) EB
إذا كان طول قطر يساوي 18 و LM=12 و ، فأوجد القياسين الآتيين مقرباً إجابتك إلى أقرب جزء من مئة، إذا لزم ذلك.
14)
15) HP
16) تزلج: سكة التزلج في الشكل المجاور تأخذ شكل قوس من دائرة، حيث جزء من قطرها، إذا كان قياس يساوي %32 من الدائرة الكاملة، فأوجد .
17) طرق: الحافة الخارجية للطريق المنحنية المبينة في الشكل المجاور جزء من التي نصف قطرها 88 ft، أوجد AB مقرباً إجابتك إلى أقرب عشر.
18) جبر: في ، إذا كان: ، DF=3x-7, FE=x+9، فأوجد قيمة x.
19) جبر: في ، إذا كان: LM=16 , PN=4x، فأوجد قيمة x.
برهان: اكتب برهاناً من النوع المحدد في كلّ من السؤالين الآتيين:
20) برهان حر للجزء الثاني من النظرية 4.2،
المعطيات: .
المطلوب: .
متروك للطالب.
21) برهان ذو عمودين للنظرية 4.3،
المعطيات:
المطلوب: .
متروك للطالب.
22) تصميم: صمَّم زيد شعاراً لمقهى كما في الشكل المجاور، إذا كانت أطوال الأوتار جميعها متساوية، فما قياس كل قوس؟ وما طول كل وتر؟
قياس كل قوس°90، وطول كل وتر 2.12ft.
23) برهان: اكتب برهاناً ذا عمودين للنظرية 4.4.
متروك للطالب.
برهان: اكتب برهاناً ذا عمودين للجزء المشار إليه من النظرية 4.5 في كل من السؤالين الآتيين:
24) إذا تساوى بعدا وترين في دائرة عن مركزها، فإن هذين الوترين متطابقان.
متروك للطالب.
25) إذا تطابق وتران في دائرة، فإن بعديهما عن مركزها متساويان.
متروك للطالب.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)





النقاشات