حل أسئلة تدرب وحل المسائل
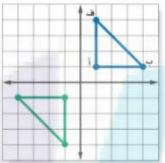
٥) انسخ المثلث أ ب ف المبين على المستوى الإحداثي ثم ارسم صورته بالدوران حول نقطة الأصل بزاوية ٢٧٠°.
ارسم الشكل بالرؤوس المعطاة، ثم ارسم صورته بعد إجراء الدوران المعطى واكتب إحداثيات رؤوسه.
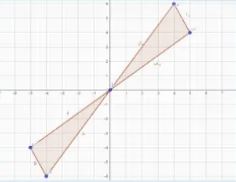
٦) المثلث أ ب ج إحداثيات رؤوسه أ (٠، ٠)، ب (٥، ٤)، جـ (٤، ٦)، بزاوية دوران ١٨٠° حول نقطة الأصل
أَ (٠، ٠)، بَ (-٥، -٤)، جـَ (-٤، -٦)
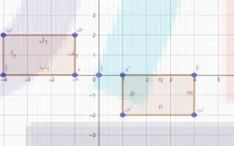
٧) المستطيل ل م ن هـ إحداثيات رؤوسه، ل (١، ٦)، م (١، ٢)، ن (٨، ٢)، هـ (٨، ٦) بزاوية دروان ٩٠° حول نقطة الأصل
لَ (-٦، ١)، مَ (-٢، ١)، نَ (-٢، ٨)، هـَ (-٦، ٨)
٨) اختيار من متعدد: إذا إجري دوران المثلت ع ص س بزاوية الدوران ١٨٠° حول نقطة الأصل فما إحداثيات النقطة ع
أ) (-١، ٥)
ب) (٥، ١)
جـ) (-٥، ١)
د) (١، -٥)
ارسم الشكل بالرؤوس المعطاة، ثم ارسم صورته بعد إجراء الدوران المعطى. واكتب إحداثيات رؤوسه.
٩) شبه المنحرف أ ب جـ د الذي إحداثيات رؤوسه: أ (٩، ٢)، ب (٧، ٧)، جـ (٥، ٧)، د (٣، ٢) زاوية الدوران ٩٠°.
أَ (-٢، ٩)، بَ (-٧، ٧)، جـَ (-٧، ٥)، دَ (-٢، ٣)
١٠) متوازي الأضلاع ح ط ي ك الذي إحداثيات رؤوسه: ح (٦، ٦)، ط (٤، ٧)، ي (١، -١)، ك (٣، -٢) زاوية الدوران ٢٧٠°.
حَ (٦، -٦)، طَ (٧، -٤)، يَ (١، -١)، كَ (-٢، -٣)
١١) يمثل المستطيل أ ب ج د الذي رؤوسه أ (-٤ ، ٠)، ب (-٤، ٢)، جـ (-١، ٢)، د ( -١، ٠) طاولة في غرفة أحمد، ويفكر في تدويرها حول نقطة الأصل بزاوية ١٨٠°.
أ) عين إحداثيات رؤوس الطاولة بعد تدويرها.
رؤوس الطاولة بعد تدويرها ١٨٠°
أَ (٤ ، ٠)، بَ (٤، -٢)، جـَ (١، -٢)، دَ ( ١، ٠)
ب) مثل الطاولة وصورها بالدوران على المستوى الإحداثي.
١٢) إعلان: يعمل مصمم فني على تكرار صورة شريحة فطيرة مخبوزة لأغراض إعلانية.
أ) أوجد صورة شريحة الفطيرة بالدوران الذي مركزه نقطة الأصل، وبزاوية ١٨٠°.
الدوران ١٨٠°
ب) عين نقطة لم تتغير صورتها بالدوران؟
النقطة الني لم يتغير صورتها بالدوران هي (٠، ٠)
جـ) ما زوايا الدوران التي يحتاجها المصمم، لاستكمال شكل الفطيرة المخبوزة كاملاً.
زوايا الدوران التي يحتاجها المصمم، لاستكمال شكل الفطيرة المخبوزة كاملاً هي : ٩٠°، ١٨٠°، ٢٧٠°.
١٣) إذا كانت النقطة أ هي صورة النقطة أ بالدوران حول نقطة الأصل بزاوية ٩٠°، وكانت النقطة أ هي النقطة أ بدوران حول نقطة الأصل بزاوية ٢٧٠°.
أ) أكمل الجدول التالي:
| النقطة أ | النقطة أَ (زاوية ٩٠°) | النقطة أَ (زاوية ٢٧٠°) |
| (٢، ٣) | (-٣، ٢) | (٣، -٢) |
| (٣، ٥) | (-٥، ٣) | (٥، -٣) |
| (٦، ٩) | (-٩، ٦) | (٩، -٦) |
ب) اكتب قاعدة الدوران التي تحول النقطة أ إلى النقطة أَ بدوران حول نقطة الأصل وفسر ذلك.
تحريك النقطة أ بزاوية محددة في اتجاه محدد ويسمى اتجاه الدوران حول نقطة ثابتة (نقطة الأصل) وتسمى مركز الدوران ويكون اتجاه الدوران في عكس اتجاه عقارب الساعة.
١٤) هـ و ع رؤوسه هـ (-٥، ٢)، و (-٣، ٦)، ع (-١، ٣)، أوجد صورة المثلث بدوران بزاوبة ١٨٠° حول النقطة (-٤، ١)
هـَ (-٧، -١)، وَ (-٥، -٤)، عَ (-٣، ٠)
١٥) إذا أجري دوران ف ص ل بزاوية ٢٧٠°حول نقطة الأصل فأصبحت إحداثيات صورته بعد الدوران فَ (١، -٢)، صَ (٥، -٣)، لَ (٤، -٥) أوجد إحداثيات رؤوس المثلث ف ص ل؟
ف (٢، ١)، ص (٣، ٥)، ل (٥، ٤)
١٦) تقنية: ابحث عن أحد التطبيقات الحاسوبية لإجراء دوران لشكل هندسي تقترحه حول نقطة الأصل بزاوية ١٨٠° . اشرح خطوات الحل
جيوجبرا: هو برنامج يختص بالهندسة التفاعلية والجبر والإحصاء وتطبيقات التفاضل والتكامل.
زاوية الدوران ١٨٠° حول نقطة الأصل.
هـ (١، ٣)، و (٣، ٢)، ع (٥، ٤)
هـَ (-١، -٣)، وَ (-٣، -٢)، عَ (-٥، -٤)
خطوات الحل:
- نحدد النقاط ونرسم مضلع متجه.
- نحدد نقطة الدوران (نقطة الأصل)
- نحدد زاوية الدوران ١٨٠°
١٧) تبرير: هل العبارة (محيط شكل رباعي يساوي محيط صورته بالدوران) صحيحة دائماً أم صحيحة أحياناً أم أنها غير صحيحة أبداً
صحيحة دائماً لأن الدوران نوع من التحويلات الهندسية التي تحافظ على الشكل وقياساته.
١٨) هندسة: ارسم شكلاً هندسياً ثم قم بتدويره حول نقطة الأصل مرة عكس عقارب الساعة ومرة مع عقارب الساعة بالزوايا (٩٠°، ١٨٠°، ٢٧٠°) ماذا تلاحظ؟
- نلاحظ عند تدوير الشكل في الزاوية ٩٠° في عكس اتجاه عقارب الساعة فإن الشكل يدور إلى الربع الثاني أما عند تدويره في اتجاه عقارب الساعة فإن الشكل يدور إلى الربع الرابع.
- نلاحظ عند تدوير الشكل في الزاوية ١٨٠° في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة فإن الشكل يدور إلى الربع الثالث.
- نلاحظ عند تدوير الشكل في الزاوية ٢٧٠° في عكس اتجاه عقارب الساعة فإن الشكل يدور إلى الربع الرابع أما عند تدويره في اتجاه عقارب الساعة فإن الشكل يدور إلى الربع الثاني.
١٩) اكتب هل هناك حالات تبقى فيها النقاط عند تدويرها ثابتة؟ اشرح ذلك.
هناك نقاط عند تدويرها تبقى ثابتة هي نقطة الأصل (٠، ٠) فعند تدويرها إلى أي زاوية فإنها تبقى ثابتة ولا تتغير.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
.JPG)
النقاشات