الدرس 5: خطة حل المسألة
حلل النتائج:
١- اشرح متى تستعمل خطة "حل مسألة أبسط".
عندما يمكن حل المسألة بطريقة تجعلك تصل إلى الإجابة باستعمال أعداد أبسط.
٢- اشرح لماذا وجد الطلاب التعامل مع ١٠٪ هو الأسهل.
حيث أنه مكن الطلاب من سهولة تقسيم ٣٠٠ إلى ٣٠ مجموعة وبهذا أصبح الحل أسهل.
٣- اكتب مسألة يمكن حلها عن طريق "حل مسألة أبسط" ثم اكتب خطوات الحل.
يصنع ٣ عمال ٣ مقاعد في ٣ أيام فما عدد المقاعد التي يصنعها ٩ عمال يعملون بهذا المعدل في ٣٠ يوماً؟
أفهم: معطيات المسألة يصنع ٣ عمال ٣ مقاعد في ٣ أيام.
خطط: استخدام حل مسألة أبسط.
حل: ٣ ÷ ٣ = ١ كل عامل يصنع مقعداً واحداً في ٣ أيام.
٣٠ ÷ ٣ = ١٠ مقاعد لكل عامل في ٣٠ يوماً.
١٠ × ٩ = ٩٠ مقعداً.
إذن يصنع ٩ عمال ٩٠ مقعداً في ٣٠ يوماً.
تحقق: إجابة معقولة إذن الإجابة صحيحة.
استعمل خطة "حل مسألة أبسط" لحل المسائل ٤ - ٦:
٤- نقود: حصل سعيد على خصم بنسبة ١٨٪ من قيمة مشترياته فإذا أراد أن يشتري بمبلغ ٢٤٦ ريالاً فما مقدار الخصم الذي يحصل عليه تقريباً؟
أفهم: معطيات المسألة كمية الخصم هم ١٨٪ من مبلغ ٢٤٦ ريال والمطلوب معرفة قيمة الخصم.
خطط: استخدام حل مسألة أبسط.
حل: ١٨ ٪ = = أي أنه تم خصم ١٨ ريال من كل ١٠٠ ريال.
وبتقسيم ٢٤٦ تكون (١٠٠+ ١٠٠ + ٤٦).
إذن نسبة خصم كل ١٠٠ هي ١٨
ونسبة خصم ٤٦ = ١٨ × ٤٦ ÷ ١٠٠ = ٨,٢
إذن إجمالي نسبة الخصم = ١٨ + ١٨ + ٨,٢ = ٤٤,٢٨ ريالاً.
تحقق: ١٨ ٪ × ٢٤٦ = ٤٤,٢٨ إذن الإجابة صحيحة.
وبطريقة التقريب: اشترى بمبلغ ٢٥٠ تقريباً والخصم ٢٠ ٪ تقريباً.
تقريباً.
٥- قراءة: قدر على أنه يقرأ نحو ١٥٠٠ صفحة في السنة فكم صفحة تقريباً يقرأ في الأسبوع؟
أفهم: معطيات المسألة: يقرأ على نحو ١٥٠٠ صفحة في السنة.
المطلوب كم صفحة تقريباً يقرأ في الأسبوع.
خطط: استخدام حل مسألة أبسط.
حل: يقرأ نحو ١٥٠٠ صفحة في السنة.
يقرأ في الشهر = ١٥٠٠ ÷ ١٢ = ١٢٥ صفحة.
يقرأ في الأسبوع = ١٢٥ ÷ ٤ = ٣١.٢٥ ≈ ٣٠ صفحة تقريباً.
تحقق: في السنة ٥٢ أسبوع تقريباً.
١٥٠٠ ÷ ٥٢ = ٢٩ صفحة تقريباً إذن الإجابة صحيحة.
٦- شوكولاتة: ينتج مصنع ١٢٠٠ حبة مغلفة من الشوكولاتة في الدقيقة الواحدة فكم حبة تقريباً ينتج في الثانية الواحدة؟
أفهم: ينتج المصنع ١٢٠٠ حبة مغلفة في الدقيقة.
المطلوب: كم حبة ينتج في الثانية الواحدة.
خطط: استخدام حل مسألة أبسط.
حل: ينتج المصنع ١٢٠٠ حبة مغلفة في الدقيقة.
ينتج في الثانية الواحدة = ١٢٠٠ ÷ ٦٠ = ٢٠ حبة.
تحقق: ٢٠ × ٦٠ = ١٢٠٠ حبة إذن الإجابة صحيحة.
استعمل الخطة المناسبة مما يأتي لحل المسائل ٧ - ١٦:
٧- ساعات: تصدر ساعة أحمد صوتاً في أسبوع واحد؟
أفهم: معطيات المسألة: تصدر الساعة صوتاً كل ساعة.
المطلوب: إيجاد عدد المرات في الأسبوع.
خطط: استخدام حل مسألة أبسط.
حل: الأسبوع يحتوي على ٧ أيام واليوم يحتوي على ٢٤ ساعة إذن يحتوي الأسبوع على ٧ × ٢٤ = ١٦٨ مرة.
وحيث أن تصدر الساعة صوت كل ساعة إذن تصدر ١ × ١٦٨ = ١٦٨ صوت خلال الأسبوع.
تحقق: ١:١ = س: س: ١٦٨، إذن س = ١٦٨. إذن الإجابة صحيحة.
٨- إطارات: الشكل أدناه يبين جزءاً من لوح خشبي.
فإذا كانت كل أقسام اللوح متساوية العرض والشكل الأول فيه مثلثاً وطول اللوح ٧٤ سم فماذا كون الشكل الأخير؟
أفهم: معطيات المسألة: كل أقسام اللوح متساوية في العرض طول اللوح ٧٤ سم.
المطلوب: الشكل الأخير.
خطط: باستعمال خطة البحث عن نمط.
حل: برسم هذا النمط وتكراره إلى أن يصل إلى ٧٤ سم.
بالنظر إلى هذا النمط نجد أن آخر شكل هو دائرة.
تحقق: برسم النمط بجد أن الإجابة صحيحة.
٩- تمرين: ركض فهد مسافة ١ كم في الأسبوع الأول و٢ كلم في الأسبوع الثاني و٤ كلم في الأسبوع الثالث وهكذا استعداداً للمشاركة في سباق الماراثون فكم كيلو متراً سيركض في الأسبوع السادس إذا استمر بالمعدل نفسه؟
أفهم: معطيات المسألة: ركض مسافة ١ كم في الأسبوع الأول ركض مسافة ٢كم في الأسبوع الثاني ركض ٤ كم في الأسبوع الثالث،
المطلوب: كم كيلو متراً سيركض في الأسبوع السادس.
خطط: باستعمال خطة البحث عن نمط.
حل: يجري فهد كل أسبوع ضعف المسافة في الأسبوع الماضي.
فإذا استمر على هذا النمط ينتج:
في الأسبوع الأول = ١ كلم.
في الأسبوع الثاني = ٢ كلم.
في الأسبوع الثالث = ٤ كلم.
في الأسبوع الرابع = ٨ كلم.
في الأسبوع الخامس = ١٦ كلم.
في الأسبوع السادس = ٣٢ كلم.
تحقق: باتباع النمط نجد أن الإجابة صحيحة.
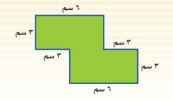
١٠- مساحة: أوجد مساحة الشكل الآتي:
أفهم: معطيات المسألة: أطوال الأضلاع كما بالشكل.
المطلوب: إيجاد المساحة.
خطط: باستعمال خطة التخمين والتحقق.
حل: نرسم قطعة مستقيمة في منتصف الشكل لكي تجعل الشكلين مستطيلات.
يكون طولها = ٣ سم.
- مساحة المستطيل ١ = الطول × العرض = ٦ × ٣ = ١٨ سم٢
- مساحة المستطيل ٢ = الطول × العرض = ٦ × ٣ = ١٨ سم٢
- مساحة المستطيلين = ١٨ + ١٨ = ٣٦ سم٢
تحقق: (٢ × ٦) × (٢ × ٦) = ١٢ × ٦ = ٣٦ سم٢ إذن الإجابة صحيحة.
١١- وشاح: تريد هند أن تجزئ شريطاً من وشاح طوله ١٨٠ سم إلى قطع طول كل منها ٥ سم لتعلقها على صدور أطفال الروضة فإذا كانت كل عملية قص تستغرق ثانية واحدة فما الوقت الذي تستغرقه عملية قص الشريط كله إلى قطع طول كل منها ٥ سم؟
أفهم: معطيات المسألة: شريط طوله ١٨٠ سم نريد قصه إلى قطع طول كل قطعة = ٥ سم. قص القطعة يستغرق ثانية.
المطلوب: إيجاد مدة قص الشريط.
خطط: باستعمال خطة تمثيل المسألة.
حل: كل ٥ سم تستغرق ثانية إذن ١٨٠ سم تستغرق؟
بقسمة ١٨٠ ÷ ٥ = ٣٦ ثانية.
تحقق: ٣٦ ثانية × ٥ سم = ١٨٠ سم.
إذن الإجابة صحيحة.
١٢- مصافحات: جرت ١٠ مصافحات في حفلة حيث صافح كل شخص جميع مرة واحدة كم كان عدد الحاضرين في الحفلة؟
أفهم: معطيات المسألة: ١٠ مصاحف في الحفلة صافح كل شخص جميع الحاضرين مرة واحدة.
المطلوب: إيجاد عدد الحاضرين.
خطط: باستعمال خطة تمثيل المسألة.
حل: بتمثيل المسألة أجد أن المصافحة تكون بين شخصين إذن عدد الحاضرين = ١٠ ÷ ٢ = ٥ أشخاص.
تحقق: بتمثيل المسألة أجد أن الإجابة صحيحة.
١٣- فطائر: التمثيل بالأعمدة أدناه يبين عدد الفطائر من كل نوع من الأنواع الموجودة في مخبز ما فكم مرة يساوي عدد فطائر الفراولة عدد فطائر الدجاج؟
أفهم: معطيات المسألة: البيانات الموضحة في التمثيل البياني:
المطلوب: كم مرة يساوي عدد فطائر الفراولة عدد فطائر الدجاج؟
خطط: باستعمال خطة مسألة أبسط.
حل: من التمثيل البياني ألاحظ أن عدد فطائر الفراولة = ٩ فطائر وعدد فطائر الدجاج = ٢ فطيرة.
إذن عدد فطائر الفراولة = ٩ ÷ ٢ = ٤,٥ فطيرة دجاج.
تحقق: ٢ × ٤,٥ = ٩ فطائر إذن الإجابة صحيحة.
١٤- زكاة: دفع راشد ١٨٥٣ ريالاً زكاة لأمواله وهذا يعادل ٢,٥ من أمواله فما المبلغ الذي دفع عنه الزكاة؟
أفهم: معطيات المسألة: المبالغ التي دفعها للزكاة = ١٨٥٣ ريالاً، يعادل = ٢,٥ ٪ من أمواله.
المطلوب: مقدار المبلغ الذي دفع زكاته.
خطط: باستعمال خطة التخمين ثم التحقق.
حل: أخمن أن المبلغ المدفوع زكاته = ٢٠٠٠٠٠ ريالاً.
إذن ستكون زكاته = ٢٠٠٠٠٠ × ٢,٥ ٪ = ٥٠٠٠ ريالاً.
إذن هذا التخمين غير صحيح.
أخمن أن المبلغ المدفوع زكاته = ٦٠٠٠٠ ريالاً.
إذن ستكون زكاته = ٦٠٠٠٠ × ٢,٥ ٪ = ١٥٠٠ ريالاً.
إذن هذا التخمين غير صحيح
أخمن أن المبلغ المدفوع = ٧٤١٢٠ ريالاً.
إذن ستكون زكاته = ٧٤١٢٠ × ٢,٥ ٪ = ١٨٥٣ ريالاً.
إذن هذا التخمين صحيح.
إذن المبلغ الذي دفع زكاته = ٧٤١٢٠ ريالاً.
تحقق: ٣٦ ثانية × ٥ سم = ١٨٠ سم.
إذن الإجابة صحيحة.
١٥- أنماط: صف النمط الآتي ثم أوجد العدد المفقود:
٤ - ١٢ - - ١٠٨ - ٣٢٤
أفهم: معطيات المسألة: النمط: ٤ - ١٢ - - ١٠٨ - ٣٢٤
المطلوب: إيجاد العدد المفقود.
خطط: باستعمال خطة البحث عن نمط.
حل: بالنظر للنمط نجد أن ٤ × ٣ = ١٢
١٠٨ × ٣ = ٣٢٤
إذن النمط هو الضرب × ٣
إذن العدد المفقود = ١٢ × ٣ = ٣٦
تحقق: ٣٦ × ٣ = ١٠٨
إذن الإجابة صحيحة.
١٦- ملصقات: مع خليل ٣٢ ملصقاً ويريد أن يعطي كل واحد من أصدقائه الأربعة العدد نفسه من الملصقات فما عدد الملصقات التي يحصل عليها كل واحد منهم؟
أفهم: معطيات المسألة: مع خليل ٣٢ طابع.
لديه ٤ أصدقاء.
كل صديق يأخذ العدد نفسه من الطوابع.
المطلوب: عدد الطوابع التي يحصل عليها كل واحد منهم.
خطط: باستعمال خطة تمثيل المسألة..
حل: ٣٢ ÷ ٤ = ٨
إذن يأخذ كل واحد منهم ٨ طوابع.
تحقق: ٨ × ٤ = ٣٢ طابع.
إذن الإجابة صحيحة.


.JPG)
.JPG)


.JPG)
النقاشات