حل أسئلة اختبار الفصل العاشر
١- ما العلاقة بين قطر الدائرة ونصف قطرها؟
ق = ٢ نق.
٢- ما العلاقة بين قطر الدائرة ومحيطها؟
محيط الدائرة = ط ق.
أوجد نصف القطر أو القطر لكل دائرة في الحالات الآتية:
٣- نق = ٩ سم.
ق = ٢ نق قطر الدائرة.
= ٢ × ٩
= ١٨
٤- ق = ٤٦ ملم.
نق =
= = ٢٣ ملم.
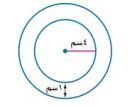
٥- اختيار من متعدد: الشكل أدناه يظهر دائرتين لهما المركز نفسه.
أي مما يأتي يمكن استعماله لإجاد محيط الدائرة الخارجية بالسنتيمترات؟
أ. ط (٤+١)
ب. (٤+١)
جـ. ٢ط (٤+١)
د. ٢(٤+١)
أوجد مساحة كل من المثلث ومتوازي الأضلاع الآتيين:
٦- .JPG)
القاعدة = ٦ وحدات، الارتفاع = ٥ وحدات.
م = ق ع
= (٦) (٥)
= (٣٠) = ١٥ وحدة٢
٧- .JPG)
م = ق ع
= ٣١ × ١١ = ٣٤١ سم٢
٨- تبرير: أيهما أكبر مساحة مثلث طول قاعدته ٨م وارتفاعه ١٢م أم مساحة مثلث طول قاعدته ٤م وارتفاعه ١٦م؟ فسر إجابتك.
مساحة مثلث طول قاعدته ٨م وارتفاعه ١٢ م أكبر.
م = ق ع = (٨) (١٢)
= (٩٦) = ٤٨ م٢ لمساحة المثلث الأول.
م = ق ع
= (٤) (١٦) = ٦٤ = ٣٢ م٢ مساحة المثلث الثاني.
٩- زراعة: حديقة عل شكل مثلث طول قاعدته ٧م وارتفاعه ٦م فإذا كان الكيس الواحد من السماد يكفي لتسميد ٢٥ م٢ منها فما عدد أكياس السماد التي تحتاج إليها لتسميد الحديقة؟
م = ق ع مساحة الحديقة.
= (٧) (٦)
= (٤٢)
= ٢١ م٢ الكيس الواحد السماد يكفي لتسميد ٢٥ م٢ إذن تحتاج كيس واحد من السماد.
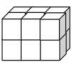
١٠- هندسة: يتكون منشور رباعي من ١٢ مكعباً أوجد أبعاده الممكنة باستعمال خطة: "إنشاء نموذج".
أفهم: تعرف على أن المنشور الرباعي يتكون من ١٢ مكعباً وأوجد أبعاد المنشور.
خطط: أنشئ نموذجاً لمعرفة أبعاد المنشور.
حل: أبعاد المنشور الممكنة هي طوله = ٣ وحدات وعرضه = ٢ وحدة.
ارتفاعه = ٢ وحدة.
تحقق: ح = ل ض ع حجم المنشور الرباعي.
= ٣ × ٢ × ٢
= ١٢ وحدة٣
إذن الإجابة صحيحة.
أوجد حجم كل من الشكلين الآتيين:
١١- .JPG)
ح = ل ض ع.
= ٧ × ٥ × ١٥
= ٥٢٥ ملم٣
١٢- .JPG)
ح = ل ض ع.
= ٦ × ٤ × ٢ = ٤٨ سم٣
١٣- برك: بركة على شكل منشور رباعي طولها ٢١م وعرضها ١٨م أوجد عدد الأمتار المكعبة من الماء التي تلزمها ليصل ارتفاع الماء فيها إلى ٩م.
ح = ل ض ع.
= ٢١ × ١٨ × ٩
= ٣٤٠٢ م٣
١٤- اختيار من متعدد: أي العبارات الآتية يعطي مساحة سطح منشور رباعي طوله ٥ وحدات وعرضه ٨ وحدات وارتفاعه ٣ وحدات؟
أ. ٢(٢٥) + ٢(٢٨) + ٢(٢٣)
ب. ٢(٥) (٢) + ٢(٥) (٣) + ٢(٨) (٣)
ج. ٢(٥) (٨) (٣)
د. (٢) (٥) (٨+٣)
أوجد مساحة سطح كل من المنشورين الآتيين:
١٥- .JPG)
س = ٢ل ض + ٢ ل ع + ٢ ض ع
= ٢ (٩) (٧) + ٢(٩) (٦) + ٢(٧) (٦)
= ١٨(٧) + ١٨(٦) + ١٤(٦)
= ١٢٦ + ١٠٨ + ٨٤
= ٣١٨ ملم٢
١٦- .JPG)
س = ٢ل ض + ٢ ل ع + ٢ ض ع
= ٢(١١) (٨) + ٢(١١) (١٧) + ٢ (٨) (١٧)
= ٢٢(٨) + ٢٢(١٧) + ١٦(١٧)
= ١٧٦ + ٣٧٤ + ٢٧٢
= ٨٢٢ سم٢
مشاركة الدرس
الاختبارات
اختبار الكتروني: اختبار الفصل العاشر
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">


النقاشات