حل أسئلة تدرب وحل المسائل
احسب مساحة كل من الاشكال الآتية وقرب الناتج إلى أقرب عشر:
٥- .JPG)
م = ق ع
= × ٢١ × ١٤
= ١٠,٥ × ١٤
= ١٤٧ سم٢
٦- .JPG)
الشكل مثلث.
م = ق ع
= × ٩,٦ × ٨
= ٤,٨ × ٨
= ٣٨,٤ ملم٢
٧- .JPG)
الشكل شبه منحرف.
م = ع (ق ١ + ق٢)
م = × ٢ × (٣,٤ + ٢,١)
م = × ٢ × ٥,٥
م = ٥,٥ سم٢
٨- .JPG)
الشكل شبه منحرف.
م = ع (ق ١ + ق٢)
م = × ٨ × (١٧,٨٥ + ١٠,٢٥)
م = × ٨ × ٢٨
م = ١١٢ م٢
٩- 
الشكل مثلث,
م = ق ع
= × ١٦,٧ × ٢٢
= ٨,٣٥ × ٢٢
= ١٨٣,٧ سم
١٠- .JPG)
الشكل شبه منحرف.
م = ع (ق ١ + ق٢)
م = × ٨,٥ × (٢٣ + ١٥)
م = × ٨,٥ × ٣٨
م = ١٦١,٥ م٢
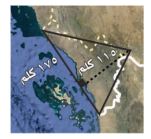
١١- جغرافيا: منطقة جازان في المملكة العربية السعودية مثلثة الشكل تقريباً كما في الشكل المجاور احسب المساحة التقريبية لها.
المنطقة على شكل مثلث.
م = ق ع
= × ١٧٥ × ١١٥
= ٨٧,٥ × ١١٥
= ١٠٠٦٢,٥ م٢
١٢- جبر: أوجد مساحة شبه منحرف طولا قاعدتيه ١٣ م، ١٥ م، وارتفاعه ٧م.
شبه منحرف طولا قاعدتيه ١٣ م، ١٥ م وارتفاعه ٧ م.
م = ع ( ق١ + ق٢)
م = × ٧ × (١٣ × ١٥)
م = × ٧ × ٢٨
م = ٩٨ م٢
جبر: احسب ارتفاع كل من الشكلين الآتيين:
١٣- 
الشكل مثلث.
م = ق ع
١١٥٠٠ = × ١٨٤ × س
٢٣٠٠٠ = ١٨٤ س
س = ١٢٥م
١٤- 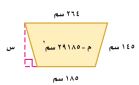
الشكل شبه منحرف.
م = ع (ق ١ + ق٢)
٢٩١٨٥ = × س × (١٨٥ + ٢٦٤)
م = ٢٩١٨٥
٢٩١٨٥ = × س × ٤٤٩
٥٨٣٧٠ = ٤٤٩ س
س = ١٣٠ م
ارسم الشكلين الآتيين، ثم احسب مساحة كل منهما.
١٥- مثلث غير قائم الزاوية ومساحته أقل من ١٢ سم٢
مثلث غير قائم الزاوية ومساحته أقل من ١٢ سم٢
م = ق ع
م = × ٤ × ٣
م = ٦ سم٢
١٦- شبه منحرف فيه زاوية قائمة ومساحته أكبر من ٤٠ سم٢
شبه منحرف مساحته أكبر من ٤٠ سم٢
م = ع (ق ١ + ق٢)
م = × ٨,٥ × (٢٣ + ١٥)
= × ٨,٥ × ٣٨
= ١٦١,٥
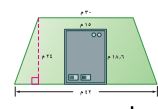
١٧- بنايات: يبين الشكل المجاور مخطط بناية تجارية مقامة على قطعة أرض على شكل شبه منحرف احسب المساحة الكلية للأرض، ثم احسب مساحة الأرض المحيطة بالبناية.
مساحة الأرض = ع (ق١ + ق٢)
= × ٢٤ ×(٤٢ + ٣٠)
= × ٢٤ × ٧٢
= ٨٦٤ م٢
مساحة المبنى = ط × ع
= ١٨,٦ × ١٥ = ٢٧٩ م٢
المساحة المحيطة بالمبنى = مساحة الأرض - مساحة المبنى.
= ٨٦٤ - ٢٧٩
= ٥٨٥ م٢
١٨- تحد: أ ب جـ مثلث، طول قاعدته ٤ وحدات، وارتفاعه ٨ وحدات د هـ ومثلث طولا قاعدته وارتفاعه ضعف طولي قاعدة وارتفاع المثلث أ ب جـ ما العلاقة بين نسبة قاعدتي المثلثين إلى نسبة مساحتيهما؟
مساحة المثلث أ ب جـ = × ق × ع
= × ٤ × ٨
= ١٦ سم٢
طول قاعدة المثلث د هـ و = ٤ × ٢ = ٨
ارتفاع المثلث د هـ و = ٨ × ٢ = ١٦
مساحة المثلث د هـ و = ق ع
= × ٨ × ١٦
= ٦٤ سم٢
مساحة المثلث د هـ و = ٤ أمثال مساحة المثلث أ ب جـ
نسبة مساحتيهما تساوي مربع نسبة قاعدتيهما.
١٩- اكتب: صف العلاقة بين مساحتي متوازي الأضلاع والمثلث اللذين لهما نفس القاعدة والارتفاع.
مساحة المثلث الذي له نفس القاعدة والارتفاع مع متوازي الأضلاع تساوي نصف مساحة متوازي الأضلاع.
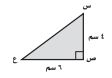
٢٠- ما مساحة المثلث س ص ع في الشكل الآتي؟
أ. ٢٤ سم٢
ب. ١٢ سم٢
ج. ١٠ سم٢
د. ٦ سم٢
مساحة المثلث = ق ع
= × ٦ × ٤ = ١٢ سم٢
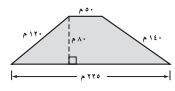
٢١- إجابة قصير: ما مساحة قطعة الأرض المبينة في الشكل الآتي؟
مساحة قطعة الأرض = ع (ق١ + ق٢)
= × ٨٠ (٢٢٥ + ٥٠)
= × ٨٠ × ٢٧٥
= × ٢٢٠٠٠
مساحة قطعة الأرض = ١١٠٠٠ م٢

.JPG)
.JPG)
.JPG)
النقاشات