حل أسئلة تدرب وحل المسائل
حل كل معادلة فيما يأتي باستعمال القانون العام مقرباً الحل إلى أقرب جزء من عشرة إذا كان ضرورياً:
١١) ٤س٢ +٥س - ٦ = ٠
س =
س =
س =
س =
س = = -٢
١٢) س٢ + ١٦ = ٠
س٢ = -١٦
١٣) ٦س٢ -١٢س +١ = ٠
س =
س =
س =
س = = ١,٩
س = = ٠,٠٩
١٤) ٥س٢ -٨س = ٦
س =
س =
س =
س = = ٢,٢
س = = - ٠,٦
١٥) ٥س٢ +٢١س = - ١٨
س =
س =
س =
س = = -١,٢
س = = -٣
١٦) ٢س٢ = ١٢س -١٨
س =
س =
س =
س = ٣
حل كل معادلة فيما يأتي، واذكر الطريقة التي استعملتها:
١٧) ٢س٢ -٨س = ١٢
القانون العام:
س =
س =
س =
س = = ٥,٢
س = = -١,٢
١٨) ٣س٢ -٢٤س = -٣٦
التحليل إلى العوامل:
٣س٢ - ٢٤س + ٣٦ = ٠
س٢ -٨س + ١٢ = ٠
(س + ٢) (س - ٦) = ٠
س = -٢
س = ٦
١٩) س٢ -٣س = ١٠
التحليل إلى العوامل:
س٢ - ٣س - ١٠ = ٠
(س + ٢) (س - ٥) = ٠
س = -٢
س = ٥
أوجد قيمة المميز لكل معادلة فيما يأتي، ثم حدد عدد حلولها الحقيقية:
٢٠) س٢ -س = ٣
س٢ -س - ٣ = ٠
ب٢ - ٤أ جـ = (-)٢ -٤ × ١ × -٣
= ١٢,٦٤ حلان حقيقيان
٢١) ٠,٥س٢ -٢س = -٢
٠,٥س٢ -٢س + ٢ = ٠
ب٢ - ٤أ جـ = (-٢)٢ -٤ × ٠,٥ × ٢
= ٠ حل واحد حقيقي.
٢٢) ٠,٢س٢ -١,٥س + ٢,٩ = ٠
٠,٢س٢ -١,٥س + ٢,٩ = ٠
ب٢ - ٤أ جـ = (-١,٥)٢ -٤ × ٠,٢ × ٢,٩
= -٠,٠٧ لا يوجد حلول حقيقية.
٢٣) مرور: تمثل المعادلة ف = ٠,٠٠٧ع + ٠,١٩ع المسافة (ف) بالأمتار التي تقطعها سيارة تسير بسرعة (ع) كلم/ساعة للتوقف تماماً مع استعمال المكابح، فإذا كانت حدود السرعة القصوى في أحد الشوارع ٨٠ كلم/ساعة، وتوقفت سيارة منذر بعد ٥٥ متراً من استعمال المكابح، فهل كانت سرعته تزيد على السرعة القصوى؟ فسر تبريرك.
ف = ٠,٠٠٧ × (٨٠)٢ + ٠,١٩ × ٨٠
ف = ٦٠
المسافة للسرعة القصوى = ٦٠ متراً.
والمسافة لـ منذر = ٥٥ متراً.
إذن سرعة منذر لا تزيد عن السرعة القصوى.
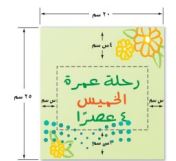
٢٤) إعلان: يعد راشد ملصقاً للإعلان عن رحلة عمرة، ويريد أن يغطي جزءاً من المساحة بنصوص كتابية.
أ) اكتب معادلة لمساحة القسم النصي.
(٢٠ - ٢س) (٢٥ - ٧س) = ٣٧٥
ب) حل المعادلة باستعمال القانون العام.
(٢٠ - ٢س) (٢٥ - ٧س) = ٠
٤٠٠ - ١٤٠ س - ٥٠س + ١٤س٢ = ٠
٥٠٠ - ١٩٠س + ١٤س٢ = ٠
س =
س =
س =
س = = ١٠
س = = ٣,٥٧
جـ) كم يجب أن تكون هوامش الملصق؟
هوامش الملصق ٧س، ٢س أي ٧٠، ٢٠
حدد دون استعمال التمثيل البياني عدد المقاطع السينية لكل دالة فيما يأتي:
٢٥) ٤,٢٥س + ٣ = -٣س٢
٣س٢ + ٤,٢٥س + ٣ = ٠
ب٢ - ٤أ جـ = (٤,٢٥)٢ -٤ × ٣ × ٣
≈ ١٧,٩
قيمة المميز سالبة، إذن لا يوجد مقاطع سينية لهذه المعاملة صفر.
٢٦) س٢ + = س
٢٥س٢ - ١٥س + ٢ = ٠
٢٥س٢ - ٥س - ١٠س + ٢ = ٠
(٥س - ٢) (٥س + ١) = ٠
س = -
س =
عدد المقاطع السينية = ٢
٢٧) ٠,٢٥س٢ + س = -١
ضربي طرفي المعادلة × ١٠٠
٢٥س٢ + ١٠٠س + ١٠٠ = ٠
س =
س =
س = = -٢
عدد المقاطع السينية = ١
حل كل معادلة فيما يأتي باستعمال القانون العام مقرباً الناتج إلى أقرب جزء من عشرة إذا كان ذلك ضرورياً:
٢٨) -٢س٢ -٧س = -١,٥
س =
س =
س =
س = = ٣,٧
س = = -٠,٢
٢٩) ٢,٣س٢ - ١,٤س = ٦,٨
س =
٢,٣س٢ - ١,٤س - ٦,٨ = ٠
س =
س =
س = = ٢,٠٥
س = = -١,٤
٣٠) س٢ -٢س = ٥
س =
س =
س =
س = = ٣,٤
س = = -١,٤
٣١) تمثيلات متعددة: سوف تكتشف الدوال الأسية في هذه المسألة:
أ) جدولياً: انسخ الجدول الآتي وأكمله:
| الزمن (ساعة) | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ |
| عدد البكتيريا | ٠٢ = ١ | ١٢ = ٢ | ٢٢ = ٤ | ٣٢ = ٨ | ٤٢ = ١٦ | ٥٢ = ٣٢ | ٦٢ = ٦٤ |
ب) بيانياً: مثل المعلومات المعطاة في الجدول بيانياً باستعمال النقاط (الزمن، عدد البكتيريا)، وهل التمثيل خطي أم تربيعي أم غير ذلك؟
التمثيل البياني ليس خطياً ولا تربيعياً،
جـ) تحليلياً: ماذا يحدث لعدد البكتيريا كل ساعة؟ اكتب دالة تمثل هذا النمط.
يتضاعف عدد البكتيريا كل ساعة د (س) = ٢س
٣٢) تحد: أوجد جميع قيم ك التي تجعل للمعادلة: "٢س٢ -٣س + ٥ك = ٠" حلين حقيقين.
ك <
٢س٢ -٣س + ٥ك = ٠
ب - ٤أ جـ = (-٣)٢ - ٤ × ٢ × ٥ك
= ٩ - ٤٠ ك
=٩ - ٤٠ ك = ٠، ك =
ك <
تبرير: بين فيما إذا كان عدد الحلول الحقيقية لكل مما يأتي حلان، أو حل واحد، أو لا يوجد حل:
٣٣) التمثيل البياني لدالة تربيعية لا تحتوي على مقطع سيني.
لا يوجد حل.
٣٤) التمثيل البياني لدالة تربيعية تمس محور السينات.
حل واحد.
٣٥) التمثيل البياني لدالة تربيعية تقطع محور السينات مرتين.
حلان.
٣٦) قيمتا كل من أ، ب أكبر من صفر، وقيمة جـ أصغر من صفر في الصيغة القياسية للدالة التربيعية.
حلان.
٣٧) مسألة مفتوحة: اكتب ٣ دوال تربيعية على أن يكون مميز الأولى موجب، ومميز الثانية سالباً، ومميز الثالثة صفراً.
- المميز موجب للدالة = د(س) = س٢ - ٤
- المميز سالب للدالة = د(س) = س٢ + ٤
- المميز صفر للدالة = د(س) = س٢ -٨س + ١٦
٣٨) اكتب: وضح طرق حل المعادلات التربيعية، وأعط مثالاً مختلفاً لكل طريقة، فسر إجابتك.
- التحليل: طريقة سهلة عندما تكون ثلاثية الحدود قابلة للتحليل.
- التمثيل البياني: يعطي فقط جذوراً تقريبية لإيجاد الجذر التربيعي طريقة سهلة عندما تكون المعادلة من الشكل أ س٢ + ب = ٠
- إكمال المربع: طريقة مضمونة لحل جميع المعادلات التربيعية.
- القانون العام: طريقة مضمونة لحل جميع المعادلات التربيعية.
٣٩) إجابة قصيرة: إذا علمت أن المثلث المجاور متطابق الضلعين، فما قيمة س؟
مجموع زوايا المثلث = ١٨٠°
وبما أن المثلث متطابق الضلعين إذن زوايا القاعدة متساوية.
س = ٦٤° أو س = = ٥٨°
٤٠) ما حلول المعادلة التربيعية ٦هـ٢ + ٦هـ = ٧٢؟
أ) ٣ أو - ٤
ب) -٣ أو ٤
جـ) لا يوجد حلول حقيقية.
د) ١٢ أو - ٤٨
٦هـ٢ + ٦هـ - ٧٢ = ٠
هـ٢ + هـ - ١٢ = ٠
(هـ - ٣) (هـ + ٤) = ٠
هـ = ٣
هـ = - ٤
الاختيار الصحيح: أ) ٣ أو -٤

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات