حل أسئلة تأكد
حل كلاً من المعادلات الآتية، وتحقق من صحة الحل:
١) ١٣س + ٢ = ٤س + ٣٨
١٣س + ٢ = ٤س + ٣٨ المعادلة الأصلية.
١٣س -٤س + ٢ = ٤س - ٤س + ٣٨ اطرح ٤س من كلا الطرفين.
٩س + ٢ - ٢ = ٣٨ - ٢ اطرح ٢ من كلا الطرفين.
٩س = ٣٦
س = ٤
التحقق:
١٣ × ٤ + ٢ = ٤ × ٤ + ٣٨
٥٤ = ٥٤
٢) ق = ق +
ق = ق + المعادلة الأصلية.
ق = ق + اطرح من كلا الطرفين.
اطرح من كلا الطرفين.
اضرب كلا الطرفين في
التحقق:
ق =
٣) ٦(ن + ٤) = -١٨
٦(ن + ٤) = -١٨ المعادلة الأصلية.
٦ن + ٢٤ = -١٨ خاصية التوزيع.
٦ن + ٢٤ - ٢٤ = -١٨ - ٢٤ اطرح ٢٤ من كلا الطرفين.
٦ن = -٤٢ أقسم كلا الطرفين على ٦.
ن = - ٧
للتحقق:
٦(-٧ + ٤) = -١٨
-١٨ = -١٨
٤) ٧ = - ١١ +٣(ب + ٥)
٧ = - ١١ +٣(ب + ٥) المعادلة الأصلية.
٧ = -١١ +٣ب + ١٥ خاصية التوزيع.
٧ - ٤ = ٣ب +٤ - ٤ اطرح ٤ من كلا الطرفين.
٣ب = ٣ أقسم كلا الطرفين على ٣.
ب = ١
للتحقق:
-١١ +٣(١ + ٥) = ٧
٧ = ٧
٥) ٥ + ٢(ن + ١) = ٢ن
٥ + ٢(ن + ١) = ٢ن المعادلة الأصلية.
٥ + ٢ن + ٢ = ٢ن خاصية التوزيع.
٢ن + ٧ = ٢ن
٦) ١٤هـ + ٦ = ٢(٥ + ٧هـ) - ٤
١٤هـ + ٦ = ٢(٥ + ٧هـ) - ٤ المعادلة الأصلية.
١٤هـ + ٦ = ١٠ + ١٤هـ - ٤ خاصية التوزيع.
١٤هـ + ٦ = ١٤هـ + ٦
بما أن الطرفين متطابقين، إذاً حلها جميع الأعداد الحقيقية.
٧) اختيار من متعدد: أوجد قيمة س التي تجعل محيطي الشكلين الآتيين متساويين:
أ) ٤
ب) ٥
جـ) ٦
د) ٧
٥س + ١ + ٢س + ٥ + ٣س + ٤ = ٤س + ٢(س + ١٣)
١٠س + ١٠ = ٤س + ٢س + ٢٦
١٠س + ١٠ = ٦س + ٢٦
١٠س - ٦س = ٢٦ - ١٠
٤س = ١٦
س = ٤
إذاً الإجابة الصحيحة أ) ٤

.JPG)
.JPG)
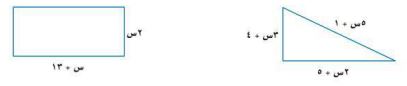


النقاشات