حل أسئلة تدرب وحل المسائل
حل كلاً من المعادلات الآتية، وتحقق من صحة الحل:
٨) ٧جـ + ١٢ = -٤جـ + ٧٨
٧جـ + ١٢ = -٤جـ + ٧٨ المعادلة الأصلية.
٧جـ + ٤جـ + ١٢ = -٤جـ + ٤جـ + ٧٨ أضف ٤ جـ إلى كلا الطرفين.
١١جـ + ١٢ - ١٢ = ٧٨ - ١٢ اطرح ١٢ من كلا الطرفين.
١١جـ = ٦٦
جـ = ٦
التحقق:
٧ × ٦ + ١٢ = -٤ × ٦ + ٧٨
٥٤ = ٥٤
٩) ٢م - ١٣ = -٨م + ٢٧
٢م - ١٣ = -٨م + ٢٧ المعادلة الأصلية.
٢م + ٨م - ١٣ = -٨م + ٨م + ٢٧ أضف ٨م إلى كلا الطرفين.
١٠م - ١٣ + ١٣ = ٢٧ + ١٣ أضف ١٣ إلى كلا الطرفين.
١٠م = ٤٠ أقسم كلا الطرفين على ١٠.
م = ٤
التحقق:
٢× ٤ - ١٣ = -٨ × ٤ + ٢٧
-٥ = -٥
١٠)
المعادلة الأصلية.
اضرب طرفي المعادلة في ٦.
ب - ٤ = ٣ب
ب - ب - ٤ = ٣ب - ب اطرح ب من كلا الطرفين.
-٤ = ٢ب أقسم كلا الطرفين على ٢.
ب = -٢
التحقق:
-١ = -١
١١) ٦(ن + ٥) = ٦٦
٦(ن + ٥) = ٦٦ المعادلة الأصلية.
٦ن + ٣٠ = ٦٦ خاصية التوزيع.
٦ن + ٣٠ - ٣٠ = ٦٦ - ٣٠ اطرح ٣٠ من كلا الطرفين.
٦ن = ٣٦ أقسم كلا الطرفي عل ٦.
ن = ٦
التحقق:
٦(٦ + ٥) = ٦ × ١١ = ٦٦
١٢) ٣(٣م - ٢) = ٢(٣م + ٣)
٣(٣م - ٢) = ٢(٣م + ٣) المعادلة الأصلية.
٩م - ٦ = ٦م + ٦ خاصية التوزيع.
٩م - ٦م - ٦ = ٦م - ٦م + ٦ اطرح ٦م من كلا الطرفين.
٣م - ٦ + ٦ = ٦ + ٦ أضف ٦ إلى كلا الطرفين.
٣م = ١٢ أقسم كلا الطرفين على ٣.
م = ٤
التحقق:
٣(٣ × ٤ - ٢) = ٢(٣ × ٤ + ٣)
٣٠ = ٣٠
١٣) ١٢ - (س + ١٥) = ٤
١٢ - (س + ١٥) = ٤
١٢ - ١٢ - (س + ١٥) = ٤ - ١٢
- (- ) (س + ١٥) = - (-٨)
س + ١٥ = ١٠
س + ١٥ - ١٥ = ١٠ - ١٥
س = -٥
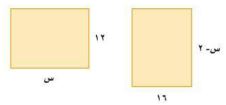
١٤) هندسة: أوجد قيمة س التي تجعل لكل من المستطيلين المجاورين المساحة نفسها.
١٦(س - ٢) = ١٢س
١٦س - ٣٢ = ١٢س خاصية التوزيع.
١٦س - ١٢س - ٣٢ = ١٢س - ١٢س اطرح ١٢س من كلا الطرفين.
٤س - ٣٢ + ٣٢ = ٠ + ٣٢ أضف ٣٢ إلى كلا الطرفين.
٤س = ٣٢ أقسم كلا الطرفين على ٤.
س = ٨
١٥) نظرية الأعداد: عددان زوجيان متتاليان، يقل أربعة أمثال أصغرهما عن مثلي أكبرهما بمقدار ١٢، فما العددان؟
افرض العددان س، س + ٢
٢(س + ٢) - ٤س = ١٢
٢س + ٤ - ٤س = ١٢
-٢س + ٤ - ٤ = ١٢ - ٤
-٢س = ٨
س = -٤
العددان هما - ٤، - ٢
١٦) نظرية الأعداد: ثلاثة أعداد صحيحة فردية متتالية يزيد مثلاً أصغرها على ثلاثة أمثال أكبرها بمقدار ١٥، فما هذه الأعداد؟
افرض الأعداد س، س + ٢، س + ٤
٢س - ٣(س + ٤) = ١٥
٢س - ٣س - ١٢ = ١٥
-س - ١٢ + ١٢ = ١٥ + ١٢
-س = ٢٧
س = -٢٧
الأعداد هي - ٢٧، - ٢٥، - ٢٣
حل كلاً من المعادلات الآتية، وتحقق من صحة الحل:
١٧) ٢س = ٢(س - ٣)
٢س = ٢(س - ٣)
٢س = ٢س -٦
ليس لها حل.
١٨) هـ - ٧ = هـ - ٢هـ + ٣
هـ - ٧ = هـ - ٢هـ + ٣
٥(هـ) - ٥(٧) = ٥(هـ) - ٥(١٢) + ٥(٣)
١٢ - ٣٥ = ١٢ + ١٥
ليس لها حل.
١٩) ٢(٤ر + ٦) = (١٢ر + ١٨)
٢(٤ر + ٦) = (١٢ر + ١٨)
٨ر + ١٢ = ٨ ر + ١٢
بما أن طرفي المعادلة متطابقين إذاً الحل جميع الأعداد الحقيقية.
٢٠) ص = ص
ص = ص
٩٦() + ٩٦(ص) = ٩٦() + ٩٦(ص)
٨ + ٣٦ ص = ٤٠ + ٦٠ص
٨ + ٣٦ص - ٣٦ص = ٤٠ + ٦٠ص - ٣٦ص
٨ - ٤٠ = ٤٠ - ٤٠ + ٢٤ص
-٣٢ = ٢٤ص
ص = -
التحقق:
(-) = (-)
- = -
٢١) (٣ر - ٢) = (ر + ٥)
٨ × (٣ر - ٢) = ٨ × (ر + ٥)
٣ر - ٢ = ٢(ر + ٥)
٣ر - ٢ = ٢ر + ١٠
٣ر -٢ر - ٢ = ٢ر - ٢ر + ١٠
ر - ٢ + ٢ = ١٠ + ٢
ر = ١٢
التحقق:
(٣(١٢) - ٢) = (١٢ + ٥)
٢٢) ٣,٢ك - ٤,٣ = ١٢,٦ك + ١٤,٥
٣,٢ك - ٤,٣ = ١٢,٦ك + ١٤,٥
٣,٢ك × ١٠ - ٤,٣ × ١٠ = × ١٠ ١٢,٦ك + ١٤,٥ × ١٠
٣٢ك - ٤٣ = ١٢٦ك + ١٤٥
٣٢ك - ١٢٦ك = ١٤٥ + ٤٣
- ٩٤ك = ١٨٨
ك = - ٢
التحقق:
٣,٢(-٢) - ٤,٣ = ١٢,٦(-٢) + ١٤,٥
٢٣) عصائر: ينفق محل للعصائر ٢٠٠ ريال يومياً نفقات ثابتة بالإضافة إلى ٢,٥ ريال تكلفة كوب العصير، فإذا بيع الكوب الواحد بمبلغ ٥ ريالات، فكم كوباً يجب أن يبيع المحل يومياً ليبدأ بتحقيق الربح؟
٥س = ٢,٥س + ٢٠٠
٢,٥س = ٢٠٠
س = ٨٠
يجب أن يبيع المحل أكثر من ٨٠ كوب.
٢٤) تمثيلات متعددة: ستكتشف في هذه المسألة حلاً للمعادلة: ٢س + ٤ = - س - ٢.
أ) بيانياً: أنشئ جدولاً يحتوي على خمس نقاط لكل من المعادلتين:
ص = ٢س + ٤، ص = - س - ٢، وعين هذه النقاط في المستوى الإحداثي.
ص = ٢س + ٤
| س | -٢ | -١ | ٠ | ١ | ٢ |
| ص | ٠ | ٢ | ٤ | ٦ | ٨ |
ص = - س - ٢
| س | -٢ | -١ | ٠ | ١ | ٢ |
| ص | ٠ | -١ | -٢ | -٣ | -٤ |
ب) جبرياً: حل المعادلة: ٢س + ٤ = - س - ٢,
٢س + ٤ = - س - ٢
٢س + س = -٢ - ٤
٣س = -٦
س = -٢
جـ) لفظياً: وضح العلاقة بين الحل الذي توصلت إليه في الفقرة (ب)، مع نقطة التقاطع للتمثيليين البيانيين في الفقرة (أ).
حل المعادلة جبرياً هو نفسه نقطة التقاطع في الرسم البياني للإحداثي السيني.
٢٥) تبرير: حل المعادلة الآتية موضحاً كل خطوة من خطوات الحل: ت = ٢ -٢[٢ت - ٣(١ - ت).
ت = ٢ -٢[٢ت - ٣(١ - ت)] المعادلة الأصلية.
ت = ٢ -٢(٢ت - ٣ - ٣ت) خاصية التوزيع.
ت = ٢ - ٤ت + ٦ - ٦ت خاصية التوزيع.
ت = ٨ - ١٠ت خاصية الجمع.
١١ت = ٨ أقسم الطرفين على ١١.
ت =
٢٦) تحد: اكتب معادلة تحتوي متغيراً في كل من طرفي إشارة المساواة بحيث يكون أحد المعاملات على الأقل كسراً، ويكون حلها - ٦، وناقش الخطوات التي اتبعتها.
٢٢س + ١ = س - ٢
٤س + ٢ = س - ٤ اضرب طرفي المعادلة في ٢.
٤س - س = -٤ -٢ خاصية الجمع.
٣س = -٦ أقسم طرفي المعادلة على ٣.
س = -٢
٢٧) تحد: أوجد قيمة ك التي تجعل كلاً من المعادلتين الآتيتين متطابقة:
أ) ك (٣س - ٢) = ٤ - ٦س
ك (٣س - ٢) = ٤ - ٦س
ك (٣س - ٢) = -٢(٣س - ٢)
ك = - ٢
ب) ١٥ص - ١٠ + ك = ٢(ك ص - ١) - ص
١٥ص - ١٠ + ك = ٢(ك ص - ١) - ص
١٥ص - ١٠ + ك = ٢ك ص - ٢ - ص
ك = ٨
٢٨) اكتب: وضح كلاً من أوجه الشبه والاختلاف بين حل معادلات تحتوي متغيرات في كلا طرفيها، وحل معادلات من خطوة واحدة أو متعددة الخطوات، تحتوي متغيرات في أحد طرفيها فقط.
- عند حل المعادلة التي تحتوي على متغير في كلا طرفيها يتم استعمال الجمع أو الطرح لفصل المتغير.
- ثم استعمال الخطوات نفسها المستعملة لحل معادلات الخطوة الواحدة أو متعددة الخطوات.
٢٩) بدأت طائرة شراعية الهبوط من ارتفاع ٢٥ متراً عن سطح الأرض بمعدل ثابت مقداره ٢متر في الثانية، فأي المعادلات الآتية تبين ارتفاع الطائرة ع بعد ن ثانية؟
أ) ع = ٢٥ن + ٢ن
ب) ع = - ٢٥ن + ٢
جـ) ع = ٢ن + ٢٥
د) ع = - ٢ن + ٢٥
٣٠) ما قيمة س التي تحقق المعادلة الآتية؟
أ) ١٦
ب) ١٤
جـ) ٦
د) -١٠

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات