حل أسئلة الاختبار التراكمي للفصل الثالث
اقرأ كل سؤال فيما يأتي، ثم اختر رمز الإجابة الصحيحة:
١) إذا كان للمستقيم ميل موجب ومقطع صادي سالب، فماذا يحدث للمقطع السيني إذا زاد كل من الميل والمقطع الصادي إلى مثليه؟
أ) يصبح المقطع السيني أربعة أمثال الأصلي.
ب) يصبح المقطع السيني مثلي الأصلي.
جـ) يصبح المقطع السيني الأصلي.
د) يبقى المقطع السيني كما هو.
٢) يبين الجدول أدناه العلاقة بين درجات الحرارة السيليزية والفهرنهايتية، فأي المعادلات الخطية الآتية تمثل هذه العلاقة؟
| الدرجات السيليزية (س) | الدرجات الفهرنهايتية (ف) |
| ١٠° | ٥٠° |
| ١٥° | ٥٩° |
| ٢٠° | ٦٨° |
| ٢٥° | ٧٧° |
| ٣٠° | ٨٦° |
أ) ف = س + ٣٥
ب) ف = س + ٤٢
جـ) ف = س + ٣٢
د) ف = س + ٢٦
٣) ميل المستقيم المار بالنقطتين (٠، ٥)، (٦، ٢) يساوي:
أ)
ب) -
جـ) ٢
د) -٢
٤) حل المعادلة: = ٥ هو:
أ)
ب)
جـ) ١٧
د) ٦٠
= ٥
١٢ × = ٥ × ١٢
س = ٦٠
٥) حل المعادلة: -٩ = ٣ت + ٦ هو:
أ) -١٥
ب) -٣
جـ) -٥
د) ٥
-٩ = ٣ت + ٦
-٩ -٦ = ٣ت + ٦ - ٦
-١٥ = ٣ت
ت = - ٥
٦) حل المعادلة: ٣(ب + ٤) = ٣٣ هو:
أ) ٧
ب) ١١
جـ) ١٥
د) ٢٦
٣(ب + ٤) = ٣٣
٣ب + ١٢ = ٣٣
٣ب + ١٢ -١٢ = ٣٣ -١٢
٣ب = ٢١
ب = ٧
أجب عن الأسئلة الآتية:
٧) مثل الدالة ص = ٢س + ٣ بيانياً.
٨) وضح كيف تحدد ما إذا كان مستقيمان متوازيين أن متعامدين.
يمكن تحديد المستقيمان المتوازيان إذا كان الميل متساوي أما إذا كان ميل أحدهما يساوي مقلوب معكوس ميل الآخر فهما متعامدان.
٩) حل المعادلة ٢(س - ١) = ٨ إذا كانت مجموعة التعويض هي: {١، ٣، ٥، ٧، ٩}.
٢(س - ١) = ٨
٢س - ٢ = ٨
٢س - ٢ + ٢ = ٨ + ٢
٢س = ١٠
س = ٥
م. جـ {٥}
١٠) اكتب كلاً من مجال ومدى العلاقة: {(١، ٣)، (٢، ٤)، (٣، ٥)، (٤، ٦)}
- المجال: {١، ٢، ٣، ٤}.
- المدى: {٣، ٤، ٥، ٦}.
١١) حدد ما إذا كانت العلاقة الآتية دالة أم لا، وفسر إجابتك: {(٨، ٤)، (٦، ٣)، (٤، ٢)، (٢، ١)، (٠، ٠)}.
نعم العلاقة يمكن أن تكون دالة؛ لأن كل عنصر في المجال ارتبط بعنصر واحد من المدى.
١٢) حل المعادلة: = ١١
= ١١
س - ٦ = ١١ أو س - ٦ = -١١
س = ١٧ أو س = -٥
م. ح: {-٥، ١٧}
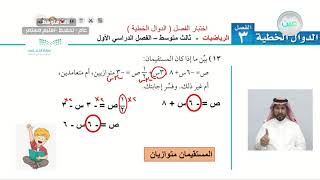
١٣) حل المعادلة: ٢٥س - ٢٢٠ = ٥س
٢٥س - ٢٢٠ = ٥س
٢٥س -٥س - ٢٢٠ = ٥س -٥س
٢٠س - ٢٢٠ = ٠
٢٠س - ٢٢٠ + ٢٢٠ = ٢٢٠
٢٠س = ٢٢٠
س = ١١
م. جـ: {١١}
١٤) اكتب المعادلة: ٢٥س - ٣٥ = ٥ص بالصورة القياسية.
- ٢٥س - ٣٥ = ٥ص
- ٢٥س - ٥ص = ٣٥
- ٥س - ص = ٧
أجب عن كل سؤال موضحاً خطوات الحل:
١٥) اشترى مروان سيارة بمبلغ ٧٥٠٠٠ ريال، إذا كانت قيمة السيارة تتناقص بمعدل ٥٠٠٠ ريال سنوياً.
أ) كون جدولاً يبين قيمة السيارة بعد عام، وعامين، و٣ أعوام، و٤ أعوام من شرائها.
| الأعوام | ١ | ٢ | ٣ | ٤ |
| قيمة السيارة | ٧٠٠٠٠ | ٦٥٠٠٠ | ٦٠٠٠٠ | ٥٥٠٠٠ |
ب) لتكن (ن) عدد السنوات منذ شراء السيارة، اكتب معادلة يمكن استعمالها لإيجاد (ق) قيمة السيارة بعد (ن) سنة.
ق = ٧٥٠٠٠ - ٥٠٠٠ن
جـ) استعمل المعادلة التي كتبتها، أوجد قيمة السيارة بعد ٨ سنوات من تاريخ شرائها.
- ق = ٧٥٠٠٠ - ٥٠٠٠ (٨)
- ق = ٣٥٠٠٠

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات