حل أسئلة اختبار الفصل الثامن
استعمل جدول القيم لتمثيل الدالتين الآتيتين بيانياً، وحدد مجالهما ومداهما:
١) ص = س٢ + ٢س + ٥
| س | -٣ | -٢ | -١ | ٠ | ١ | ١٢ |
| ص | ٨ | ٥ | ٤ | ٥ | ٨ | ١٣ |
المجال = جميع الأعداد الحقيقية،
المدى = {ص | ص > ٤}
٢) ص = ٢س٢ -٣س + ١
| س | -٢ | -١ | ٠ | ١ | ٢ | ٣ |
| ص | ١٥ | ٦ | ١ | ٠ | ٣ | ١٠ |
المجال = جميع الأعداد الحقيقية.
المدى = {ص | ص > ١}
لتكن الدالة ص = س٢ -٧س + ٦
٣) حدد إذا كان للدالة قيمة عظمى أم قيمة صغرى.
قيمة صغرى لأن قيمة أ موجبة.
٤) أوجد القيمة العظمى أو القيمة الصغرى للدالة.
= ٣,٥
ص = (٣,٥)٢ - ٣,٥ × ٧ + ٦
ص = - ٦,٢٥
القيمة الصغرى = - ٦,٢٥
٥) حدد مجال الدالة ومداها.
المجال = جميع الأعداد الحقيقية.
المدى = {ص | ص - ٦,٢٥}
حل كل من المعادلتين الآتيتين بيانياً، وإذا لك تكن الجذور أعداداً صحيحة فقدرها إلى أقرب جزء من عشرة.
٦) س٢ + ٧س + ١٠ = ٠
س = -٥، -٢
٧) س٢ -٥ = -٣س
س = -٤,٢، ١,٢
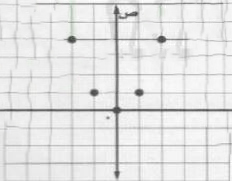
٨) اختيار من متعدد: أي المعادلات الآتية تعبر عن الدالة الممثلة بيانياً أدناه؟
أ) ص = -٣س٢
ب) ص = ٣س٢ + ١
جـ) ص = س٢ + ٢
د) ص = -٣س٢ + ٢
حل كل من المعادلتين الآتيتين باستعمال إكمال المربع:
٩) س٢ - س - ٦ = ٠
س٢ - س - ٦ = ٠
(س - ٣) (س + ٢) = ٠
س = ٣
س = -٢
١٠) ٢س٢ - ٣٦ = -٦س
٢س٢ + ٦س - ٣٦ = ٠
س٢ + ٣س - ١٨ = ٠
س٢ + ٣س = ١٨
()٢ =
س٢ + ٣س + = ١٨ +
(س + )٢ = ٢٠,٢٥
س + = +٤,٥
س = ٤,٥ -
س = ٣
س = -٤,٥ -
س = -٦
حل كل من المعادلتين الآتيتين باستعمال القانون العام، مقرباً الحل إلى أقرب جزء من عشرة إذا لزم الأمر.
١١) س٢ - س - ٣٠ = ٠
س٢ - س - ٣٠ = ٠
س =
س =
س =
س = = ٦
س = = - ٥
١٢) ٢س٢ + س - ١٥ = ٠
٢س٢ + س - ١٥ = ٠
س =
س =
س =
س = = ٣
س = = - ٢,٥
١٣) كرة سلة: سدد نواف كرة السلة نحو المرمى، وفق المعادلة ع = - ١٦ن + ٦٠ن + ٣٠، حيث تمثل (ع) ارتفاع الكرة بعد (ن) ثانية، كم تبقى الكرة في الهواء؟
-١٦ن٢ + ٦٠ن + ٣٠ = ٠
س =
س =
س =
س = = ٤,٢
٤,٢ ثانية تقريباً
١٤) مثل الدالة: ص = ٣س٢ بيانياً، أوجد المقطع الصادي، وحدد مجالها ومداها.
المقطع الصادي = صفر.
المجال = جميع الأعداد الحقيقية.
المدى = {ص | ص > ٠}
١٥) اختيار من متعدد: أي مما يلي يعد تحليلاً تاماً للعبارة ٤س٢ - ٨س - ١٢ إلى عواملها؟
أ) ٤(س - ٣) (س + ١)
ب) (٤س + ١٢) (س - ١)
جـ) ٤(س + ٣) (س - ١)
د) (س - ٣) (٤س + ٤)
٤س٢ - ٨س - ١٢ = ٠
(٤س٢ -٢س - ٣) = ٠
٤(س + ١) (س - ٣) = ٠
الاختيار الصحيح: أ) ٤(س + ١) (س - ٣) = ٠
١٦) أوجد مساحة المستطيل أدناه.
مساحة المستطيل = الطول × العرض:
= (س + ٣) (س + ١٢)
= س٢ + ١٢س + ٣س + ٣٦
= (س٢ + ١٥س + ٣٦) سم٢
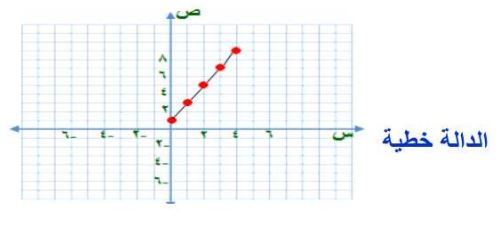
١٧) مثل مجموعة الأزواج المرتبة الآتية بيانياً:
{(-٢، ٤)، (-١، ١)، (٠، ٠)، (١، ١)، (٢، ٤)}، وحدد فيما إذا كانت تمثل دالة خطية أم تربيعية.
دالة تربيعية.
١٨) ابحث عن النمط في الجدول الآتي لتحديد أفضل نموذج دالة لوصف البيانات: خطية أم تربيعية، فسر إجابتك.
| س | ٠ | ١ | ٢ | ٣ | ٤ |
| ص | ١ | ٣ | ٥ | ٧ | ٩ |
مشاركة الدرس
الاختبارات
اختبار الكتروني: اختبار الفصل الثامن
Warning (2): Undefined array key "percent_w" [APP/View/Elements/lesson/exams.ctp, line 20]" aria-valuemin="0" aria-valuemax="100">

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)



النقاشات